Линейный источник в бесконечной пластине

Линейный источник теплоты мощностью q с равномерным распределением по толщине пластины движется с постоянной скоростью v прямолинейно из точки Оо в направлении оси х. Граничные плоскости z=0 и z=d отдают теплоту в окружающую среду, при этом коэффициент теплоотдачи равен a .

Уравнение, описывающее приращение температуры в пластине, получим аналогично случаю для полубесконечного тела. Приращение температуры в точке A(x,y) от мгновенного линейного источника, который действовал в точке О₁ , составит

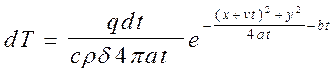
Интегрируя от 0 до t_н , получим

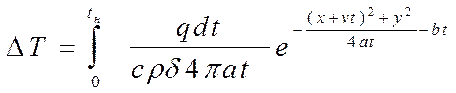
В этом уравнении выражается приращение температуры в пластине на стадии теплонасыщения. В предельном состоянии распространения тепла, ко-

гда t_н®¥ , уравнение принимает вид

,

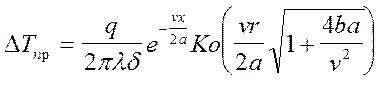где b=2a/(crd) ;

;

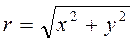Ко(u) – функция Бесселя 1-ого рода нулевого порядка для аргумента u, табулирована.

Для практических расчетов на ЭВМ с достаточной точностью приемлема приближенная формула

.

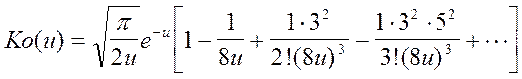Качественно картины распределения приращения температуры в пластине и на плоскости хОу подобны. Однако из-за стесненных условий теплоотвода изотермы в пластине более вытянуты.