Температурные поля от неподвижных источников

Решение дифференциального уравнения теплопроводности для мгновенного точечного источника в бесконечном теле приводит к уравнению

,

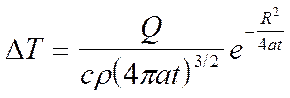где DT¾ приращение температуры в рассматриваемой точке с координатами x,y,z.; t – время, отсчитываемое от момента включения источника с количеством теплоты Q ; 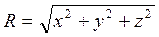¾ расстояние рассматриваемой точки от начала координат, помещенного в точку ввода источника.

Распределение температуры при распространении теплоты от мгновенного источника Q, приложенного в начале координат О на поверхности полубесконечного тела, будет аналогично случаю бесконечного тела. Т.к. теплообмен на границе xOy отсутствует и теплота распространяется только в одну сторону от плоскости xOy , то возможно использование уравнения для бесконечного тела с удвоением величины Q

.

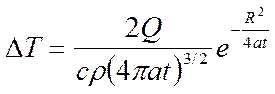Теплоотдачей в этом случае можно пренебречь

Приращение температуры прямо пропорционально количеству введенной теплоты. Температура в любой точке, кроме О, вначале повышается, достигает максимума и далее убывает, причем скорость нагрева всегда выше скорости охлаждения по абсолютной величине.

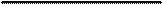
T

R=0

R₁

R2

t

В точке О температура в начальный момент равна бесконечности и скорость охлаждения максимальна.

Приращение температуры в пластине от мгновенного линейного источника Q , равномерно распределенного по толщине пластины d , не зависит от координаты z и с учетом теплоотдачи с поверхности пластины находится из уравнения

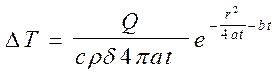
где r² = x² + y² – квадрат расстояния от рассматриваемой точки до места ввода источника .

Приращение температуры в стержне от мгновенного плоского источника Q , равномерно распределенного по площади поперечного сечения стержня F, не зависит от координат z и y и находится из уравнения

,

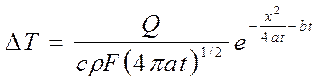где х – расстояние от места ввода источника до данной точки .

Изменение температуры во времени в пластине и стержне качественно протекает так же, как и в полубесконечном теле. Однако распространение температуры менее свободно в пластине и, тем более, в стержне. Процесс изменения температуры во времени происходит в пластине и стержне медленней.