Точечный источник на поверхности полубесконечного тела
Точечный источник теплоты постоянной мощности q движется с постоянной скоростью v прямолинейно из точки Оо в направлении оси х.

Допустим, что с момента движения источника прошло время tн и он находится в точке О. Вместе с источником перемещается подвижная система координат, начало которой совпадает с источником теплоты , т.е. с точкой О. Требуется определить приращение точки A(x,y,z).
Для этого запишем приращение температуры в точке А от мгновенного точечного источника, который действовал в течение времени dt в точке О1 . С момента выделения теплоты в точке О прошло время t. Используем уравнение для мгновенного источника и, полагая Q=qdt, а расстояние 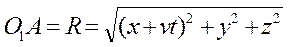 , получим
, получим
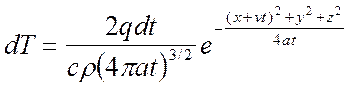
Суммируем приращения температуры от всех элементарных источников теплоты на линни Оо. Интергирование ведем в пределах от 0 до tн .
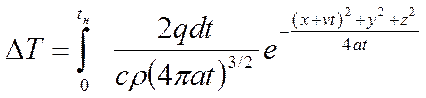
Точное аналитическое решение этого уравнения весьма затруднительно и на практике решение находится с помощью номограмм.
После продолжительного действия источника теплоты температура в подвижной системе координат перестает изменяться во времени. Такое предельное состояние распространения тепла достигается при tн®¥. В этом случае получается точное аналитическое решение для приращения температуры
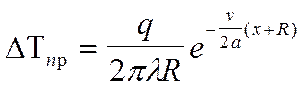
Температурное поле предельного состояния симметрично относительно оси Ох. Изотермы на поверхности xOy представляют собой овальные кривые , сгущенные впереди источника. При vR/2a ®0 изотермы близки к окружностям. Изотермические поверхности внутри тела образуются вращением изотерм вокруг оси Ох.

 Y Y
Y Y
 |  |


 X
X  Z
Z
Рассмотрим распределение температур в плоскости xOz и параллельных ей плоскостях.
 DТ
DТ
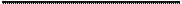 |  |
у=0

 у=1
у=1
 у=2
у=2
 х
х
Температура точек при приближении источника резко возрастает, достигает максимума и далее убывает с меньшей скоростью. Чем дальше удалена точка от оси Ох , тем позже достигается максимум температуры после прохождения источника через проекцию точки на оси Ох и тем он меньше.
Дата добавления: 2016-10-26; просмотров: 2128;











