Исключение фигуры погрешностей методом биссектрис
Метод биссектрис применяется при обсервациях по однородным линиям положения (например: 3 визуальных пеленга).
Если ориентиры находятся по одну сторону горизонта (разность между крайними пеленгами менее 180°), то вероятнейшее обсервованное место может находиться вне фигуры погрешностей и, в этом случае, следует повторить наблюдения.
Если ориентиры расположены по всему горизонту, то вероятнейшее место находится внутри фигуры погрешностей в точке пересечения биссектрис внутренних углов (рис. 24.11).
При определении места судна по высотам 3-х светил для отыскания вероятнейшего места при получении фигуры (треугольника) погрешностей используют правило освещенности сторон «…вероятнейшее место находится в точке пересечения биссектрис углов вершин треугольника, стороны которого имеют одинаковую освещенность…».
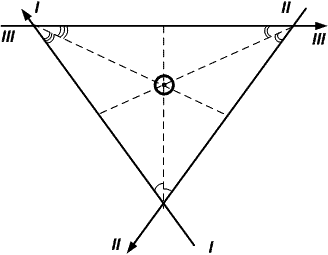
Рис. 24.11. Нахождение вероятнейшего места судна
при расположении ориентиров по всему горизонту
На рис. 24.12 место судна определено по 3-м звездам и все они находятся по одну сторону горизонта (с правого борта). Внутренние углы треугольника (их стороны) имеют разную освещенность, поэтому, по правилу освещенности вероятное место судна внутри фигуры находиться не может (если не исключаются систематические погрешности, т.к. при наличии только случайных погрешностей вероятное место будет внутри фигуры на пересечении противомедиан).
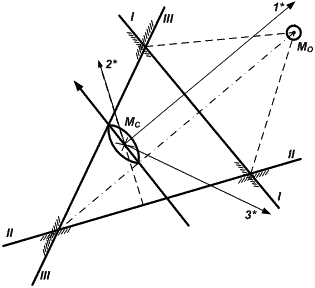
Рис. 24.12. Нахождение вероятнейшего места при расположении
ориентиров по одну сторону горизонта
На рис. 24.13 место судна определено по 3-м звездам, расположенным по всему горизонту.
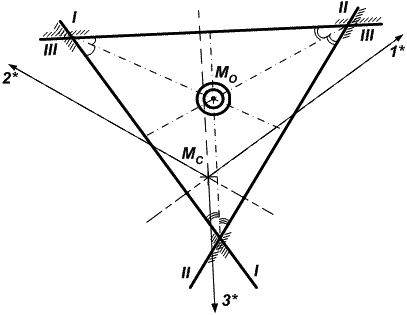
Рис. 24.13. Нахождение вероятнейшего места при расположении
ориентиров по всему горизонту
Стороны внутренних углов фигуры (треугольника) погрешностей имеют одинаковую освещенность, и вероятнейшее место в этом случае находится внутри фигуры на пересечении биссектрис внутренних углов. Причем это будет справедливо и при наличии только случайных погрешностей (точка пересечения противомедиан).
Для оценки точности полученного места можно использовать приближенную формулу
| МО3ЛП ≈ МО2ЛП | (24.3) |
| где | МО2ЛП – радиальная (круговая) СКП, рассчитанная для 2-х линий положения, угол пересечения которых ближе всего к 90°. |
Радиальную (круговую) СКП обсервованного по 4-м линиям положения можно определить по приближенной формуле:
| МО4ЛП ≈ mЛП | (24.4) |
где mЛП – СКП линии положения.
Дата добавления: 2021-01-26; просмотров: 737;











