Задачи на расчет допустимого времени плавания по счислению

<105 106 107108109 110 111 >

Рассчитать допустимое время плавания по счислению (t_доп), чтобы не превысить допустимое значение радиальной СКП (М_доп), если радиальная СКП последней, принятой к счислению обсервации (М₀), а коэффициент точности счисления (К_C) (значения К_C, М₀, М_доп → см. условия задач 1÷10).

№ задач	Условие	Ответ	№ задач	Условие	Ответ
К_C	М₀ (мили)	М_доп (мили)	t_доп (мин)	К_C	М₀ (мили)	М_доп (мили)	t_доп (мин)
1 2 3 4 5 6 7 8 9 10	0,5 0,5 0,6 0,6 0,7 0,7 0,8 0,8 0,9 0,9	0,5 0,9 0,2 0,6 0,4 0,7 0,1 0,6 0,3 0,3	2,0 1,0 0,3 1,2 0,7 1,4 0,3 1,4 0,4 1,5	900 75 32 180 70 180 30 150 25 160	11 12 13 14 15 16 17 18 19 20	1,2 1,2 1,3 1,3 1,4 1,4 1,5 1,5 1,6 1,6	0,1 0,5 0,2 0,7 0,1 0,2 0,2 0,4 0,2 0,8	0,3 1,9 0,3 2,0 0,5 2,0 0,4 1,8 0,5 1,5	20 140 15 125 30 121 20 100 25 70

Периодичность определений места судна (мин.)
(допустимое время плавания по счислению)

Таблица 24.3

D_кр до опасности (мили)	М_доп(мили) М₀(мили)	Коэффициент точности счисления (К_C)
0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2,0
	0,2/0,1
	0,3/0,1 0,3/0,2	48 38	40 32	35 27	30 24	27 21	24 19	22 17	20 16	19 15	17 14	16 13	15 12	14 11	13 11	13 10	12 10
	0,4/0,1 0,4/0,2 0,4/0,3	66 59 45	55 49 38	47 42 32	41 37 28	37 33 25	33 30 23	30 27 21	28 25 19	26 23 17	24 21 16	22 20 15	21 19 14	20 17 13	18 16 13	17 16 12	17 15 11
	0,5/0,1 0,5/0,2 0,5/0,3 0,5/0,4	84 78 68 51	70 65 57 43	60 55 49 37	52 49 43 32	47 44 38 29	42 39 34 26	38 36 31 23	35 33 29 21	32 30 26 20	30 28 24 18	28 26 23 17	26 25 21 16	25 23 20 15	23 22 19 14	22 21 17 14	21 20 17 13
	0,6/0,1 0,6/0,2 0,6/0,3 0,6/0,4 0,6/0,5	101 97 89 77 57	85 81 74 64 47	72 69 64 55 41	63 61 56 48 36	56 54 49 43 32	51 48 45 38 28	46 44 40 35 26	42 40 37 32 24	39 37 34 29 22	36 35 32 27 20	34 32 30 26 20	32 30 28 24 18	30 29 26 23 17	28 27 25 21 16	27 26 23 20 15	25 24 22 19 14
	0,7/0,1 0,7/0,2 0,7/0,3 0,7/0,4 0,7/0,5 0,7/0,6	118 115 108 98 84 62	99 96 90 82 70 52	85 82 77 70 60 44	74 72 68 62 52 39	66 64 60 55 47 34	59 57 54 49 42 31	54 52 49 45 38 28	49 48 45 41 35 26	46 44 42 38 32 24	42 41 39 35 30 22	40 38 36 33 28 21	37 36 34 31 26 19	35 34 32 29 25 18	33 32 30 27 23 17	31 30 29 26 22 16	30 29 27 25 21 15
	0,8/0,1 0,8/0,2 0,8/0,3 0,8/0,4 0,8/0,5 0,8/0,6 0,8/0,7	151 144 132 119 107 91 66	113 111 106 99 89 76 55	97 95 91 85 76 65 47	85 83 79 74 67 57 41	76 74 71 66 59 50 37	68 66 64 59 54 45 33	62 60 58 54 49 41 30	57 55 53 49 45 38 28	52 51 49 46 41 35 26	49 47 45 42 38 32 24	45 44 42 40 36 30 22	43 41 40 37 33 28 21	40 39 37 35 31 27 20	38 37 35 33 30 25 18	36 35 33 31 28 24 17	34 33 32 30 27 23 17
	0,9/0,1 0,9/0,2 0,9/0,3 0,9/0,4 0,9/0,5 0,9/0,6 0,9/0,7 0,9/0,8	192 185 173 156 134 108 97 71	133 128 120 115 107 96 81 59	110 107 104 99 92 82 69 50	96 94 91 86 80 72 61 44	85 84 81 77 71 64 54 37	77 75 73 69 64 57 48 35	70 68 66 63 58 52 44 32	64 63 61 58 53 48 40 29	59 58 56 53 49 44 37 24	55 54 52 49 46 41 35 25	51 50 48 46 43 38 32 24	48 47 45 43 40 36 30 21	45 44 43 41 38 34 29 21	43 42 40 38 36 32 27 20	40 40 38 36 34 30 26 19	38 38 36 35 32 29 24 18
	1,0/0,1 1,0/0,2 1,0/0,3 1,0/0,4 1,0/0,5 1,0/0,6 1,0/0,7 1,0/0,8 1,0/0,9	238 230 218 202 180 154 122 103 75	165 160 152 140 125 114 102 86 62	121 120 117 112 106 98 87 73 53	107 105 102 98 93 86 77 64 47	95 93 91 87 82 76 68 57 42	85 84 82 79 74 69 61 51 37	78 76 74 71 67 62 56 47 34	71 70 68 65 62 57 51 43 31	66 65 63 60 57 53 47 40 29	61 60 58 56 53 49 44 37 27	57 56 55 52 49 46 41 34 25	53 52 51 49 46 43 38 32 23	50 49 48 46 44 40 36 30 22	47 46 45 44 41 38 34 29 21	45 44 43 41 39 36 32 27 20	43 42 41 39 37 34 31 26 19
	1,1/0,1 1,1/0,2 1,1/0,3 1,1/0,4 1,1/0,5 1,1/0,6 1,1/0,7 1,1/0,8 1,1/0,9 1,1/1,0	288 281 269 252 230 204 173 137 108 79	200 195 187 175 160 142 120 108 90 65	147 143 137 129 120 113 104 92 77 56	117 116 113 110 105 99 91 79 68 49	104 103 101 98 93 88 81 71 60 44	94 93 91 88 84 79 73 65 54 39	85 84 82 80 76 72 66 59 49 36	78 77 76 73 70 66 61 54 45 33	72 71 70 68 65 61 56 50 42 30	67 66 65 63 60 56 52 46 39 28	63 62 60 59 56 53 48 43 36 26	59 58 57 55 52 49 45 40 34 25	55 54 53 52 49 46 43 38 32 23	52 51 50 49 47 44 40 36 30 22	49 49 48 46 44 42 38 34 29 21	47 46 45 44 42 40 36 32 27 20
	1,2/0,1 1,2/0,2 1,2/0,3 1,2/0,4 1,2/0,5 1,2/0,6 1,2/0,7 1,2/0,8 1,2/0,9 1,2/1,0 1,2/1,1	343 336 324 307 286 259 228 192 151 114 82	238 233 225 213 198 180 158 133 113 95 69	175 171 165 157 146 132 119 110 97 81 59	134 131 127 120 117 111 104 96 85 71 51	114 113 111 108 104 99 93 85 76 63 46	102 101 100 97 94 89 84 77 68 57 41	93 92 91 88 85 81 76 70 62 52 37	85 85 83 81 78 74 70 64 57 47 34	79 78 77 75 72 69 64 59 52 44 32	73 72 71 69 67 64 60 55 49 41 29	68 67 66 65 62 59 56 51 45 38 27	64 63 62 61 58 56 52 48 43 36 26	60 60 59 57 55 52 49 45 40 33 24	57 56 55 54 52 49 46 43 38 32 23	54 53 52 51 49 47 44 40 36 30 22	51 51 50 48 46 45 42 38 34 28 21
	1,3/0,1 1,3/0,2 1,3/0,3 1,3/0,4 1,3/0,5 1,3/0,6 1,3/0,7 1,3/0,8 1,3/0,9 1,3/1,0 1,3/1,1 1,3/1,2	403 396 384 367 346 319 288 252 211 166 119 86	280 275 267 255 240 222 200 175 130 119 99 71	206 202 196 187 176 163 147 129 115 102 85 61	158 155 150 143 135 125 117 110 101 89 74 54	124 122 120 118 114 110 104 98 89 79 66 48	111 110 108 106 103 99 94 88 80 71 59 43	101 100 99 96 94 90 85 80 73 65 54 39	93 92 90 88 86 82 78 73 67 59 49 36	85 85 83 82 79 76 72 68 62 55 46 33	79 79 77 76 73 71 67 63 57 51 42 31	74 73 72 71 69 66 63 59 54 47 40 29	69 69 68 66 64 62 59 55 50 44 37 27	66 65 64 62 61 58 55 52 47 42 35 25	62 61 60 59 57 55 52 49 45 40 33 24	58 58 57 56 54 52 49 46 42 37 31 23	56 55 54 53 51 49 47 44 40 36 30 21
	1,4/0,1 1,4/0,2 1,4/0,3 1,4/0,4 1,4/0,5 1,4/0,6 1,4/0,7 1,4/0,8 1,4/0,9 1,4/1,0 1,4/1,1 1,4/1,2 1,4/1,3	468 458 449 432 410 384 353 317 276 230 180 125 89	325 320 312 300 285 267 245 220 192 160 125 103 74	239 235 229 220 209 196 180 162 141 120 106 88 64	183 180 175 169 160 150 138 127 115 105 93 77 56	144 142 139 133 127 120 115 109 102 93 82 69 49	120 119 117 115 112 108 104 98 92 84 74 62 41	109 108 107 105 102 99 94 90 84 76 67 56 40	100 99 98 96 93 90 87 82 77 70 62 52 37	92 91 90 88 86 83 80 76 71 65 57 48 34	85 85 84 82 80 77 74 70 66 60 53 44 32	80 79 78 77 75 72 69 66 61 56 49 41 30	75 74 73 72 70 68 65 62 57 52 46 39 28	70 70 69 68 66 64 61 58 54 49 44 36 26	66 66 65 64 62 60 56 55 51 47 41 34 25	63 63 62 61 59 57 55 52 48 44 39 33 23	60 59 58 57 56 54 52 49 46 42 37 31 22
	1,5/0,1 1,5/0,2 1,5/0,3 1,5/0,4 1,5/0,5 1,5/0,6 1,5/0,7 1,5/0,8 1,5/0,9 1,5/1,0 1,5/1,1 1,5/1,2 1,5/1,3 1,5/1,4	538 530 518 502 480 454 422 386 346 300 250 194 134 92	373 368 360 348 333 315 293 268 240 208 173 135 107 77	274 271 264 256 245 231 216 197 176 153 127 110 92 66	210 207 203 196 188 177 165 151 135 120 109 96 80 58	166 164 160 155 148 140 130 119 114 106 97 86 71 51	134 133 130 125 120 118 114 109 103 96 87 77 64 46	117 116 115 113 110 107 103 99 94 87 79 70 58 42	107 106 105 103 101 98 95 91 86 80 73 64 53 38	99 98 97 95 93 91 87 84 79 74 67 59 49 36	92 91 90 89 87 84 81 78 73 68 62 55 46 33	86 85 84 83 81 79 76 73 69 64 58 51 43 31	80 80 79 77 76 74 71 70 64 60 55 48 40 29	75 75 74 73 71 69 67 64 61 56 51 45 38 27	71 71 70 69 67 65 63 60 57 53 49 43 36 26	68 67 66 65 64 62 60 57 54 50 46 41 34 24	64 64 63 62 61 59 57 54 51 48 44 39 32 23
	1,6/0,1 1,6/0,2 1,6/0,3 1,6/0,4 1,6/0,5 1,6/0,6 1,6/0,7 1,6/0,8 1,6/0,9 1,6/1,0 1,6/1,1 1,6/1,2 1,6/1,3 1,6/1,4 1,6/1,5	612 605 593 576 554 528 497 461 420 374 324 269 209 144 95	425 420 412 400 385 367 345 320 292 260 225 187 145 111 80	312 309 302 294 283 269 253 235 214 191 165 137 114 95 68	239 236 232 225 217 206 194 180 164 146 127 113 100 83 60	189 187 183 178 171 163 153 142 130 119 111 101 89 74 53	153 151 148 144 139 132 124 119 113 107 100 91 80 66 48	126 125 122 120 118 116 112 108 103 97 91 82 73 60 43	114 113 112 111 109 106 103 99 94 89 83 76 67 55 40	105 105 104 102 100 98 95 91 87 82 77 70 61 51 37	98 97 96 95 93 91 88 85 81 76 71 65 57 47 34	91 91 90 89 87 85 82 79 76 71 66 60 53 44 32	86 85 84 83 81 79 77 74 71 67 62 57 50 41 30	81 80 79 78 77 75 73 70 67 63 59 53 52 39 28	76 76 75 74 72 71 69 66 63 59 55 50 44 37 27	72 72 71 70 69 67 65 63 59 56 52 48 42 35 25	69 68 67 66 65 64 62 59 57 54 50 45 40 33 24
	1,7/0,1 1,7/0,2 1,7/0,3 1,7/0,4 1,7/0,5 1,7/0,6 1,7/0,7 1,7/0,8 1,7/0,9 1,7/1,0 1,7/1,1 1,7/1,2 1,7/1,3 1,7/1,4 1,7/1,5 1,7/1,6	691 684 672 655 634 607 576 540 499 454 403 348 288 223 154 98	480 475 467 455 440 422 400 375 347 315 280 242 200 155 114 82	353 349 343 334 323 310 294 276 255 231 206 178 147 118 98 70	271 267 263 256 248 237 225 211 195 177 158 136 117 103 86 62	213 211 207 202 196 187 178 167 154 140 124 115 104 92 76 55	173 171 168 164 158 152 144 135 125 118 111 103 94 83 69 49	143 141 139 135 131 125 120 117 112 107 101 94 89 75 62 45	121 120 119 118 116 114 111 107 103 98 93 86 78 69 57 41	112 111 110 109 107 105 102 99 95 91 85 79 72 64 53 38	104 103 102 101 99 97 95 92 88 84 79 74 67 59 49 35	97 96 96 94 93 91 89 86 82 79 74 69 63 55 46 33	91 90 90 89 87 85 83 80 77 74 69 65 59 52 43 31	86 85 84 83 82 80 78 76 73 69 65 61 55 49 40 29	81 80 80 79 77 76 74 71 69 65 62 57 52 46 38 27	77 76 75 74 73 72 70 68 65 62 58 54 49 44 36 26	73 72 72 71 70 68 66 64 62 59 56 52 47 41 34 25
	1,8/0,1 1,8/0,2 1,8/0,3 1,8/0,4 1,8/0,5 1,8/0,6 1,8/0,7 1,8/0,8 1,8/0,9 1,8/1,0 1,8/1,1 1,8/1,2 1,8/1,3 1,8/1,4 1,8/1,5 1,8/1,6 1,8/1,7	775 768 756 739 718 691 660 624 583 538 487 432 372 307 238 163 101	538 533 525 513 498 480 458 433 405 373 338 300 258 213 165 118 85	396 392 386 377 366 353 337 318 298 274 249 220 190 157 121 101 72	303 300 295 289 280 270 258 244 228 210 190 169 145 120 107 88 63	239 237 233 228 221 213 204 193 180 166 150 133 119 108 95 79 56	194 192 189 185 179 173 165 156 146 134 122 115 107 97 85 71 51	160 159 156 153 148 143 136 129 120 117 111 105 97 88 78 64 46	135 133 131 128 125 120 118 115 111 107 102 96 89 81 71 59 42	118 118 117 116 114 112 109 106 103 99 94 88 82 75 66 54 39	110 110 109 107 106 104 102 99 95 92 87 82 76 69 61 50 36	103 102 101 100 99 97 95 92 89 86 81 77 71 65 57 47 34	96 96 95 94 93 91 89 86 84 80 76 72 67 61 53 44 32	91 90 89 88 87 86 84 81 79 75 72 68 63 59 50 42 30	86 85 85 84 82 81 79 77 74 71 68 64 59 54 47 39 28	81 81 80 79 78 77 75 73 70 68 64 61 56 51 45 37 27	77 77 76 75 74 73 71 69 67 64 61 57 53 48 43 35 25
	1,9/0,1 1,9/0,2 1,9/0,3 1,9/0,4 1,9/0,5 1,9/0,6 1,9/0,7 1,9/0,8 1,9/0,9 1,9/1,0 1,9/1,1 1,9/1,2 1,9/1,3 1,9/1,4 1,9/1,5 1,9/1,6 1,9/1,7 1,9/1,8	864 857 845 828 806 780 749 713 672 626 576 521 461 396 324 252 173 104	600 595 587 575 560 542 520 495 467 435 400 362 320 275 227 175 120 87	441 437 431 422 411 398 382 364 343 320 294 266 235 202 167 129 104 74	338 335 330 323 315 305 293 278 263 245 225 202 180 155 128 110 91 65	267 264 261 256 249 241 231 220 207 193 178 161 142 122 111 98 81 58	216 214 211 207 202 195 187 178 168 157 144 130 119 110 100 88 73 52	179 177 175 171 167 161 155 147 139 129 117 115 108 100 91 80 66 47	150 149 147 144 140 135 130 124 120 115 111 105 99 92 83 73 61 43	128 127 125 122 120 119 116 114 110 107 102 97 91 85 77 68 56 40	116 116 115 114 112 110 108 106 102 99 95 90 85 79 71 63 52 37	108 108 107 106 105 103 101 98 96 92 89 84 79 73 67 59 48 35	102 101 101 100 98 97 95 92 90 87 83 80 74 69 62 55 45 32	96 95 95 94 92 91 89 87 84 81 78 74 70 65 61 52 43 31	90 90 89 88 87 86 84 82 80 77 74 70 66 61 56 49 40 29	86 85 85 84 83 81 80 78 75 73 70 66 63 58 53 46 38 27	81 81 80 80 79 77 76 74 72 69 66 63 59 55 50 44 36 26
	2,0/0,1 2,0/0,2 2,0/0,3 2,0/0,4 2,0/0,5 2,0/0,6 2,0/0,7 2,0/0,8 2,0/0,9 2,0/1,0 2,0/1,1 2,0/1,2 2,0/1,3 2,0/1,4 2,0/1,5 2,0/1,6 2,0/1,7 2,0/1,8 2,0/1,9	958 950 938 922 900 874 842 806 766 720 670 614 554 490 420 346 266 182 107	665 660 652 640 625 607 585 560 532 500 465 427 385 340 292 240 185 127 89	489 485 479 473 459 446 430 411 391 367 342 313 283 250 214 176 136 107 76	374 371 367 360 352 341 329 315 299 281 262 240 217 191 164 135 113 93 67	296 293 290 284 278 270 260 249 236 222 207 190 171 151 130 114 100 83 59	239 238 235 230 225 218 211 202 191 180 167 154 139 122 113 103 90 75 54	198 196 194 190 186 180 174 167 158 149 138 127 118 111 103 94 82 68 49	166 165 163 160 156 152 146 140 133 125 119 114 109 102 94 86 75 62 45	142 141 139 136 133 129 125 119 118 114 110 105 100 94 87 79 69 57 41	122 121 120 120 119 117 115 112 109 106 102 98 93 87 81 73 65 53 38	114 114 113 112 111 109 107 105 102 99 95 91 87 82 76 69 60 50 36	107 107 106 105 104 102 100 98 96 93 89 86 81 77 71 64 56 47 33	101 100 100 99 98 96 94 92 90 87 84 81 77 72 67 61 53 44 31	95 95 94 93 92 91 89 87 85 82 81 76 72 68 63 57 50 42 30	90 90 89 88 87 86 85 84 81 78 75 72 69 64 60 54 48 39 28	86 85 85 84 83 82 80 79 77 74 72 69 65 61 57 51 45 37 27

Таблица предназначена для определения промежутка времени (в мин.) плавания по счислению после последней (принятой к счислению) обсервации в течение которого радиальная (круговая) СКП текущего места судна еще не превысит допустимое значение радиальной (круговой) СКП места (М_доп).

Входными аргументами в таблицу являются:

1. Кратчайшее расстояние (D_кр) до навигационной опасности или берега (от 10 до 100 миль, через каждые 5 миль).

2. Допустимое (по требованиям ИМО) значение радиальной (круговой) СКП места судна (М_доп) (от 0,2 мили до 2,0 мили, через каждые 0,1 мили).

3. Значение радиальной (круговой) СКП последнего (принятого к счислению) обсервованного места судна (М_O) (от 0,1 мили до 1,9 мили, через каждые 0,1 мили).

4. Значение коэффициента точности счисления (К_C) (от 0,5 до 2,0, через 0,1).

Например: Если К_C = 1,5, М_O = 0,3 мили, D_кр = 55 миль (М_доп = 1,1 мили) то Δt_доп = 60 мин.

Рекомендации по анализу счисления пути судна

В практике судовождения могут встретиться случаи, когда с достаточной уверенностью нельзя сделать заключение о достоверности обсервованного или счислимого места судна. В таких случаях, до получения достоверной информации, используется опыт хорошей морской практики.

Рассмотрим несколько примеров.

1. Одновременно (или почти одновременно) получили две обсервации, места которых на МНК не совпадают. Какому из этих мест отдать предпочтение, если точность их (М_O1 и М_O2) одинакова? (рис. 24.19).

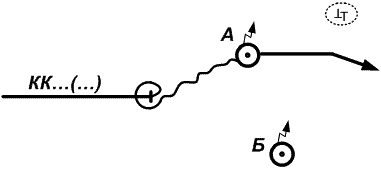
Рис. 24.19. Считай себя ближе к опасности

Оценив реальную навигационную обстановку, к дальнейшему счислению следует принимать обсервацию в точке А, которая ближе всего находится к навигационной опасности. «…Всегда считай себя ближе к опасности» – это неписанное правило должно соблюдаться всегда, чтобы избежать навигационного происшествия (посадка на мель, выход на опасные глубины и пр.).

2. При определении места судна по 3-м (и более) линиям положения при прокладке их на карте получили фигуру погрешности (рис. 24.20).

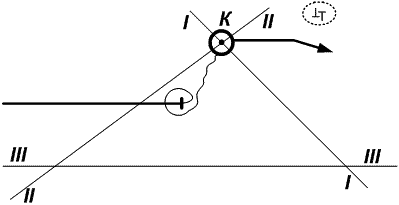
Рис. 24.20. Считай себя ближе к опасности

Оценив навигационную обстановку, считаем, что обсервованное место находится в точке пересечения ЛП I – I и ЛП II – II точка К. Ведь именно эта точка лежит ближе всего к навигационной опасности. Повторив измерения навигационных параметров, или использовав другие способы определения места, окончательно принимаем решение о достоверности обсервации.

(В данном случае предварительно сделали вывод, что в 3-й ЛП имелся промах или в измерении НП или в их обработке, или в прокладке на карте).

3. Если при определении места судна (рис. 24.21) обсервованное место находится в пределах площади круга, с центром в счислимой точке на время обсервации и радиусом R = М_СЧ, то можно сделать вывод, что счисление пути судна велось правильно и к счислению принимается обсервованное место без осреднения со счислимым.

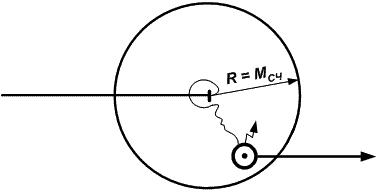
Рис. 24.21. Счислению можно доверить

Если же при определении места судна значение полученной невязки С = М_СЧ + М_O – это говорит о том, что счисление пути судна ведется некачественно (но могут быть и неточности в обсервованном месте). В данном случае к дальнейшему счислению следует принимать вероятнейшее место, получаемое осреднением счислимого и обсервованного мест.

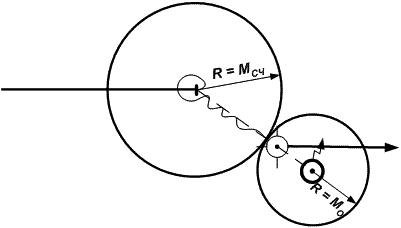
Рис. 24.22. Счислению доверить нельзя

4. Если радиальная (круговая) СКП обсервованного места М_O в три и более раза выше (точнее) радиальной (круговой) СКП счислимого места М_СЧ на момент обсервации, то к дальнейшему счислению принимают «чисто» координаты обсервованного места и не отыскивают вероятнейшее место осреднением со счислимым местом (рис. 24.23).

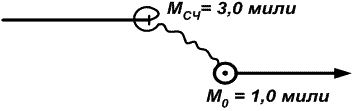
Рис. 24.23. Счисление от обсервации (3М_O ≥ М_СЧ)

Если же значения М_O и М_СЧ соизмеримы по величине (3М_O < М_СЧ), то к дальнейшему счислению принимают вероятнейшее место, отыскиваемое осреднением обсервованного (точка О) и счислимого (точка С) мест (рис. 24.24).

Из примера на рис. 24.24 очевидно, что вероятнейшее место (точка Д) точнее (М_В = 0,8 мили) и обсервованного (М_O = 1,0 мили) и счислимого (М_СЧ = 1,6 мили) мест.

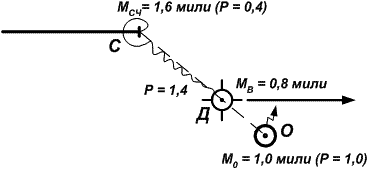
Рис. 24.24. Счисление от вероятнейшего места (3М_O < М_СЧ)

5. Если при определении места величина невязки С превышает утроенную радиальную (круговую) СКП счислимого места (М_СЧ), т.е. С > 3 М_СЧ (P = 99,9%) следует проверить графическое счисление пути судна от последней, принятой к счислению, обсервации.

При отсутствии ошибок (промахов) в счислении, следует повторить измерения, а если результат останется таким же – определить место судна другим способом.

Если и в этом случае результат останется прежним – обсервацию принять во внимание, но к дальнейшему счислению не принимать до получения уверенной надежной обсервации.

Выводы

1. Отыскание вероятнейшего места судна среди разнородных обсерваций, приведенных к одному моменту, и счислимого места производится последовательным попарным применением центрографического приема.

2. Центрографический прием – деление отрезка, соединяющего два места (приведенных к одному моменту) на части, обратно пропорциональные весам этих мест или прямо пропорционально квадратам их СКП.

3. Радиальная (круговая) СКП вероятнейшего места судна будет всегда меньше наименьшей радиальной (круговой) СКП принятых к осреднению мест, т.е. вероятнейшее место более точное, чем каждое место по отдельности.

4. Для получения более точного и надежного обсервованного места судна, необходимо иметь не две, а три и более линий положения, что дает, при условии их пересечения в одной (почти в одной) точке, полновесную обсервацию с более высокой точностью, чем при наличии всего двух линий положения.

5. Если при прокладке на карте линии положения образуют фигуру погрешности, то вероятное обсервованное место судна находится методом биссектрис или центрографическим методом.

6. Частота определений места судна в море должна быть такой, чтобы погрешность текущего места судна не превышала допустимую предельную погрешность с заданной вероятностью.

Примечание: Самоконтроль знаний по теме проводится по тестовым заданиям к главе на базе приложения «Компьютерная система тестирования знаний «OPENTEST».

<105 106 107108109 110 111 >

Дата добавления: 2021-01-26; просмотров: 440;