Какому из этих мест отдать предпочтение и взять за исходное место для дальнейшего счисления пути судна?
В подобном случае нельзя однозначно отдавать предпочтение конкретно какому-либо из имеемых мест (А, Б или С). В таких случаях необходимо произвести объединение всех этих мест и отыскать вероятнейшее место, которое будет иметь более высокую точность, чем каждое, отдельно взятое из этих мест (и в этом мы убедимся далее).
Для нахождения на путевой МНК вероятнейшего места и расчета его точности необходимо (рис. 24.2):
1. Нанести на карту счислимое место (точка А) на время последней обсервации и обсервованные места (Б – на момент времени Т1 и С – на момент времени Т2).
2. Привести обсервованные места к одному (как правило – последнему) моменту времени (Б → Б′). Таким образом, все полученные места А, Б′ и С будут соответствовать одному моменту времени – Т2.
3. Рассчитать радиальную (круговую) СКП каждого из этих мест (МсчА = 1,0 мили, МоБ = 0,7 мили, МоС = 0,7 мили).
4. Рассчитать вес каждого места.
Вес Р – величина безразмерная и характеризует степень доверия к месту. Чем больше вес места, тем оно достовернее, тем оно точнее.
Математически вес места определяется формулой:
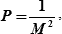
| (24.1) |
| где | М – радиальная (круговая) СКП места судна (МСЧ или М0), для которого рассчитывается его вес. |
Для нашего примера:
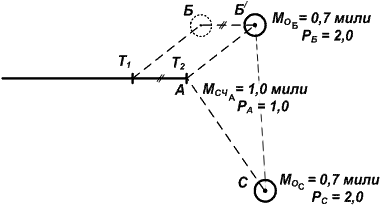
Рис. 24.2. Приведение мест к одному моменту
- место А → МсчА = 1,0 мили → 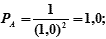
- место Б → МоБ = 0,7 мили → 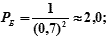
- место С → МоС = 0,7 мили → 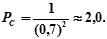
5. Соединить места А и Б′ (или А и С, или Б′ и С) отрезком прямой АБ (АС, Б′С).
Представим, что отрезок АБ (рис. 24.3) является рычагом весов, с обоих концов которого подвешены грузы весом:
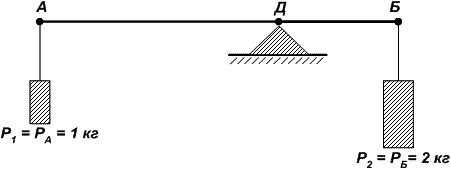
Рис. 24.3. Соотношение плеч и весов
- в точке А → Р1 = РА = 1 кг и
- в точке Б → Р2 = РБ = 2 кг.
Для равновесного положения рычага АБ точку опоры (точку Д) надо выбрать так, чтобы плечи АД и ДБ были обратно пропорциональны весу подвешенных грузов. Точка опоры (точка равновесия Д) будет всегда ближе к более тяжелому грузу, а к точке опоры (точке Д) будет приложен суммарный вес грузов РД = РА + РБ = 3 кг.
Именно в этом и заключается принцип центрографического приема, суть которого: «… для отыскания вероятнейшего места нужно отрезок АБ разделить на части, обратно пропорциональные весам точек А и Б. Вес равновесной точки равен сумме весов точек А и Б…»
Делается это так (рис. 24.4):
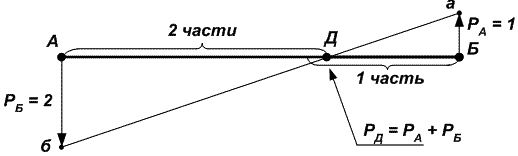
Рис. 24.4. Центрографический прием отыскания вероятнейшего места
- из точки А перпендикулярно отрезку АБ проводится линия (вверх или вниз безразлично), на которой откладывается отрезок Аб, равный весу точки Б → РБ в произвольно принятом масштабе (РБ = 2,0 – 2 см);
- из точки Б параллельно Аб (
 АБ), но в обратную сторону, проводится линия, на которой откладывается отрезок Ба, равный весу точки А → РА = 1,0 – в том же масштабе, что и РБ (Ба ~ РА = 1,0 ~ 1 см);
АБ), но в обратную сторону, проводится линия, на которой откладывается отрезок Ба, равный весу точки А → РА = 1,0 – в том же масштабе, что и РБ (Ба ~ РА = 1,0 ~ 1 см); - соединяются точки б и а прямой линией аб. Точка пересечения линии аб с отрезком АБ даст вероятнейшее из 2-х мест (А и Б) место → точку Д. Вес этого места Д равен сумме весов РА и РБ, т.е. РД = 3,0.
…или так (рис. 24.5):

Рис. 24.5. Отыскание вероятнейшего места обратно-пропорциональным методом
- рассчитывается суммарный вес двух мест (А и Б), из которых определяется вероятное место: РД = РА + РБ = 3;
- отрезок АБ разбивается на число частей равных весу РД (на 3 части);
- находится точка Д, как отстоящая от точки Б на 1 часть, а от точки А – на 2 части (обратно пропорционально весам мест А и Б).
Полученная точка Д и есть вероятнейшее место из 2-х мест А и Б, принятых к осреднению.
Следует помнить, что вероятнейшее место будет всегда ближе к месту, имеющему больший вес.
Если веса мест одинаковы (РА = РБ), то вероятнейшее место находится посредине отрезка АБ.
Если к осреднению принимается еще и 3-е место (точка С), то далее поступают следующим образом (рис. 24.6):
- соединяются прямой линией места Д и С;
- рассчитывается суммарный вес этих двух мест: РF = РД + РС = 5,0;
- отрезок ДС разбивается на число частей, равных РF (5 частей);
- находится точка F, как отстоящая от точки С на 3 части, а от точки Д – на 2 части (обратно пропорционально весам мест Д и С).
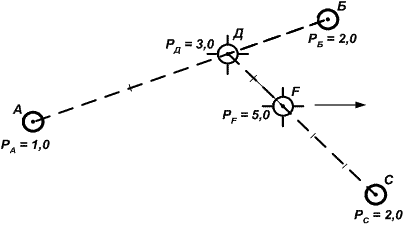
Рис. 24.6. Нахождение вероятнейшего места из трех мест
Полученная таким образом точка F и будет вероятнейшим местом из всех 3-х мест, принятых к осреднению.
Именно из этой точки на путевой МНК необходимо осуществлять дальнейшее счисление пути судна.
Вероятнейшее место на МНК условно обозначается как «  ».
».
Вес этого места (F) равен сумме весов всех мест, принятых к осреднению (РF = РА + РБ + РС = 5).
Радиальная (круговая) СКП вероятнейшего места рассчитывается по формуле:
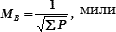
| (24.2) |
где ΣР – сумма весов мест, принятых к осреднению.
Для нашего примера 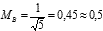 (мили) и стало очевидно, что радиальная (круговая) СКП вероятнейшего места (МВ = 0,5 мили) будет всегда меньше наименьшей радиальной (круговой) СКП принятых к осреднению мест (0,7 мили) → см. табл. 24.1.
(мили) и стало очевидно, что радиальная (круговая) СКП вероятнейшего места (МВ = 0,5 мили) будет всегда меньше наименьшей радиальной (круговой) СКП принятых к осреднению мест (0,7 мили) → см. табл. 24.1.
Радиальная погрешность осредненного места
(из табл. 4.17. «МТ-2000»)
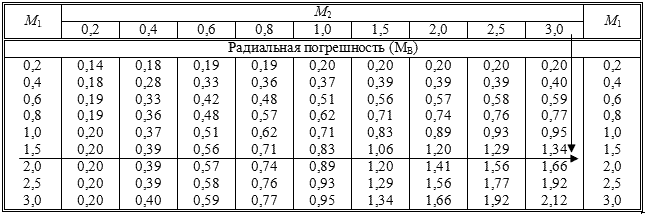
Таблица 24.1.
Примечание:
Размерность величин М1, М2, и МВ одинакова.
| Пример: | Определить радиальную СКП вероятнейшего места судна, полученного путем осреднения счислимого и обсервованного мест, оцениваемых радиальными СКП: М1 = 1,5 мили, М2 = 3,0 мили. |
| Решение: | По М1 = 1,5 мили и М2 = 3,0 мили из таблицы выбираем МВ = 1,34 мили ≈ 1,3 мили. |
Из практики судовождения принято, что:
- если радиальная (круговая) СКП одного из мест (счислимого или обсервованного) в 3 и более раза превышает наименьшее значение радиальной (круговой) СКП из всех других мест принимаемых к осреднению, то данное место из осреднения исключается.
На рис. 24.7 вероятнейшее место F определено осреднением 3-х обсервованных мест (Б, С и Д), а счислимое место А из осреднения исключено, т.к. его СКП (МсчА = 3,2 мили) более чем в 3 раза превышает наименьшую СКП из всех имеемых мест (МоД = 0,6 мили).
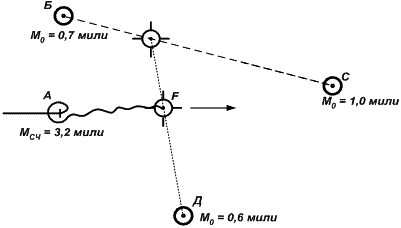
Рис. 24.7. Нахождение вероятнейшего места из четырех мест
Задача: Дано: МСЧ = 3,4 мили, М01 = 6,4 мили, М02 = 2,7 мили, МВ – ?
Решение: РСЧ = 0,087, Р01 = 0,024, Р02 = 0,137, ΣРС = 0,248
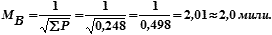
Дата добавления: 2021-01-26; просмотров: 614;











