Примеры решения задач на нахождение логическиx форм

Для нахождения логической формы выражения естественного языка необходимо:

(1) перевести это выражение на ЯЛФРТ;

(2) записать перевод в символическом виде;

(3) заменить нелогические константы переменными соответствующих категорий; при этом необходимо следить, чтобы ни одна индивидная переменная из вновь вводимых не оказалась в области действия квантора, связывающего эту переменную.

Пример 2.14. Найти логическую форму высказывания:

Параллелограмм, диагонали которого равны друг другу, является прямоугольником.

1. Пропозициональная форма

Для нахождения пропозициональной формы необходимо перевести данное высказывание на язык логики высказываний, то есть найти такую ППФ ЯЛВ, которая имеет тот же смысл, что и записанное в условии задачи предложение русского языка. Высказывание, выражаемое данным предложением русского языка, является теоремой геометрии, то есть высказыванием, истинность которого устанавливается путем особого вида логического рассуждения – доказательства; а всякая теорема геометрии (согласно Евклиду) выражается ППФ ЯЛВ вида: (А®В),

где: А – символ метаязыка, обозначающий ППФ ЯЛВ, выражающую «то, что дано» в теореме;

В – символ метаязыка, обозначающий ППФ ЯЛВ, выражающую «то, что требуется доказать» в теореме;

( ) ® использованы автонимно.

Для нахождения ППФ ЯЛВ, обозначенных символами А и В, проводим «анализ теоремы», то есть выясняем, что дано в теореме и что в ней требуется доказать.

L M Дано: KLMN – параллелограмм;

KM – диагональ KLMN;

LN – диагональ KLMN;

KM равно LN по длине.

Требуется доказать:

K N KLMN – прямоугольник.

Таким образом, ППФ ЯЛВ, обозначаемая символом А и являющаяся антецедентом импликации, представляет собой конъюнкцию четырех предложений:

А₁: данная геометрическая фигура KLMN есть параллелограмм;

А₂: данный отрезок KM есть диагональ данной геометрической фигуры KLMN;

А₃: данный отрезок LN есть другая диагональ данной геометрической фигуры KLMN;

А₄: данный отрезок KM равен по длине другому данному отрезку LN.

ППФ ЯЛВ, обозначаемая символом В и являющаяся консеквентом импликации, представляет собой следующее предложение:

B: данная геометрическая фигура KLMN есть прямоугольник.

Тогда исходное высказывание будет представлено ППФ ЯЛВ:

((А₁ÙА₂)ÙА₃)ÙА₄®В,

а его логическая форма – формулой:

((p₁Ùp₂)Ùp₃)Ùp₄®q

(скобки опущены в соответствии с соглашением о скобках).

Полученная пропозициональная форма содержит только пропозициональные переменные.

Таблица, представляющая истинностную функцию, выражаемую данной формой, содержит 2⁵=32 строки, в которых записываются наборы значений пяти пропозициональных переменных. Пропозициональная форма примет значение л только в одной строке, где антецедент импликации ((p₁Ùp₂)Ùp₃)Ùp₄ принимает значение и, а консеквент q – л. Следовательно, в этой строчке переменным приписываются следующие значения истинности: p₁ – и; p₂ – и; p₃ – и; p₄ – и; q – л. В остальных строках пропозициональная форма примет значение и. Однако мы знаем, что данное в условии задачи высказывание является теоремой, то есть всегда истинным высказыванием; и поскольку пропозициональная форма этой теоремы не является всегда истинной, истинность этой теоремы зависит от того, какие конкретно предложения подставляются вместо пропозициональных переменных в ее пропозициональную форму. Следовательно, истинность данной теоремы обусловлена связями между терминами, входящими в состав элементарных предложений, подставляемых в пропозициональную форму вместо пропозициональных переменных, а значит, для доказательства теоремы необходимо выявить состав элементарных предложений, входящих в перевод теоремы на ЯЛВ, т.е. найти ее предикатную форму.

2. Предикатная форма

При определении предикатной формы обращаем внимание на то, что в данной теореме идет речь о любых геометрических фигурах, а поэтому в составе выражающего данное высказывание предложения нет имен; следовательно, простые предложения А₁, А₂, А₃, А₄ и В должны бытьзаменены предикаторами.

Составим список имен, предикаторов и атомарных предложений, необходимых для перевода исходного высказывания на ЯЛП1⁼:

имена: нет;

атомарные предложения: нет;

предикаторы: x – геометрическая фигура А¹(x);

x – параллелограмм В¹(x);

x – прямоугольник С¹(x);

x –отрезок 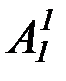(x);

x – диагональ у А²(x,у);

x равно у по длине В²(x,у);

x = у x = у.

Здесь «x равно у по длине» означает «х и у совпадают при наложении»; знак равенства является логической константой в ЯЛП1⁼.

Заменяем в приведенном выше переводе данного высказывания на ЯЛВ предложения А₁, А₂, А₃, А₄ и В соответствующими предикаторами; получаем пропозициональную форму с индивидными переменными:

(((((x – параллелограмм Ù у – диагональ x ) Ù z – диагональ x) Ù Ø у=z) Ù у равно z по длине)® x – прямоугольник),

где: х пробегает по геометрическим фигурам, у и z пробегают по отрезкам.

В естественном языке это выражение (составной неэлементарный предикатор) читается так:

если x – параллелограмм и у – диагональ x, и z – диагональ x, и у и z – разныедиагонали, и у и z–равные по длине отрезки, то x – прямоугольник.

Исходное высказывание естественного языка утверждает нечто о любых геометрических фигурах и любых отрезках; поэтому перевод его на ЯЛП1⁼ получается путем связывания всех именных переменных в составном предикаторе кванторами общности:

"_{x -}_{геометрическая фигура}"_у-_{отрезок}"_z-_{отрезок}(((((x – параллелограмм Ù у – диагональ x ) Ù z – диагональ x) Ù Ø у=z) Ù у равно z по длине)® x – прямоугольник).

Запишем составной предикатор на символическом языке:

(((((В¹(x)ÙА²(у,x))ÙА²(z,x))ÙØ у=z)ÙВ²(у,z))®С¹(x)).

Перевод исходного высказывания естественного языка на ЯЛП1⁼ представляется ППФ:

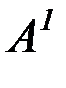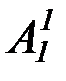"_(x)"_{( у)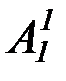}"₍_z₎(((((В¹(x)ÙА²(у,x))ÙА²(z,x))ÙØу=z)ÙВ²(у,z))®С¹(x)).

Для получения предикатной формы заменим в полученном переводе все нелогические (предикатные) константы предикатными переменными; для этого заменим символы: А на P, B на Q, С на R:

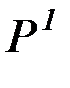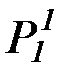"_(x)"_{( у)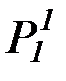}"₍_z₎(((((Q¹(x)ÙP²(у,x))ÙP²(z,x))ÙØу=z)ÙQ²(у,z))®R¹(x)).

Полученное выражение является предикатной формой данного в условии задачи высказывания.

Пример 2.15.Найти логическую форму высказывания:

«Никакие житейские блага не будут нам приятны, если мы пользуемся ими одни, не деля их с друзьями» (Э. Роттердамский).

1. Пропозициональная форма

Данное высказывание является моральной сентенцией, то есть фиксирует правило морали, а всякое правило представляется в ЯЛВ правильно построенной формулой вида:

(А®В),

где: А – символ метаязыка, обозначающий ППФ ЯЛВ, выражающую ситуацию, к которой данное правило применимо;

В – символ метаязыка, обозначающий ППФ ЯЛВ, выражающую необходимое условие выполнения правила (в данном случае – моральную оценку ситуации);

( ) ® использованы автонимно.

В отличие от теоремы, то есть истинного (на некоторой предметной области) высказывания, правило фиксируется условным высказыванием, которое не является всегда истинным, но должно быть выполнимым и опровержимым на некоторой предметной области. В случае истинности импликативного высказывания правило считается выполненным, в случае ложности – нарушенным, или невыполненным.

Рассматриваем данное высказывание как состоящее из трех простых и обозначаем простые предложения символами:

А₁: мы пользуемся житейским благами одни;

А₂: мы делимся житейскими благами с друзьями;

В: нам приятны житейские блага.

Тогда данное высказывание будет представлено ППФ ЯЛВ: А₁ÙØ А₂ ®Ø В (скобки опущены в соответствии с соглашением о скобках).

Заменяя нелогические постоянные А₁, А₂ и В пропозициональными переменными, получаем пропозициональную форму исходного высказывания: p₁ÙØ p₂® Øq.

Данная форма принимает значение л только в одной строчке из восьми в таблице истинности, а именно в той строчке, в которой антецедент импликации p₁ÙØ p₂ принимает значение и, а консеквент Øq – л; следовательно, в этой строчке переменным приписываются следующие значения истинности: p₁– и, p₂ – л, q – и. Значит, данное правило будет нарушено только в одном случае: когда предложение А₁ истинно, А₂ ложно и В истинно, то есть: когда мы пользуемся житейским благами одни и мы не делимся житейскими благами с друзьями, а нам приятны эти житейские блага. В остальных семи возможных случаях значений истинности пропозициональных переменных пропозициональная форма принимает значение и, то есть данное правило будет выполнено.

2. Предикатная форма

Составим список имен и предикаторов, необходимых для перевода исходного высказывания на ЯЛП1⁼:

имена: нет (слово «мы» здесь не называет конкретных людей, а поэтому выполняет роль индивидной переменной);

атомарные предложения: нет;

предикаторы:

x – человек А¹(x);

x – житейское благо В¹(x);

x пользуется у А²(x,у);

x – друг у В²(x,у);

x приятно у С²(x,у);

x делится у с z А³(x,y,z);

x = у x = у.

Заменяем в приведенном выше переводе данного высказывания на ЯЛВ предложения А₁, А₂ и В соответствующими предикаторами; получаем пропозициональную форму с индивидными переменными:

((((x пользуется у Ù z – друг x) ÙØ x=z) ÙØ x делится у с z) ®Ø у приятно x).

(x пробегает по предметной области «люди», у пробегает по предметной области «житейские блага», область изменения z совпадает с областью изменения переменной x)

Запишем составной предикатор на символическом языке:

((((А²(x,у)Ù В²(z,x))ÙØ x=z)ÙØ А³(x,y,z ))® Ø С²(y,x)).

Поскольку данное высказывание естественного языка предполагается относящимся ко всем людям и ко всем житейским благам, индивидные переменные в составном предикаторе связываются кванторами общности.

Перевод исходного высказывания естественного языка на ЯЛП1⁼ представляется ППФ:

"_А1_(x)"_А1₍_z₎"_В1_(у)((((А²(x,у)ÙВ²(z,x))ÙØx=z)ÙØ А³(x,y,z))®Ø С²(y,x)).

Для получения предикатной формы заменим в ППФ все нелогические (предикатные) константы предикатными переменными:

"_Р1_(x)"_Р1₍_z₎"_Q1_(у)((((P²(x,у)ÙQ²(z,x))ÙØx=z)ÙØ P³(x,y,z))®Ø R²(y,x)).

Полученное выражение является предикатной формой данного в условии задачи высказывания.

Пример 2.16. Найти логическую форму высказывания:

В русском языке частица «не» пишется с существительным слитно, если без частицы «не» существительное не употребляется.

1. Пропозициональная форма

Данное высказывание является правилом правописания русского языка, поэтому его перевод на ЯЛВ представляется ППФ вида:

(А®В),

где: А – символ метаязыка, обозначающий ППФ ЯЛВ, выражающую ситуацию, к которой данное правило применимо;

В – символ метаязыка, обозначающий ППФ ЯЛВ, выражающую необходимое условие выполнения данного правила;

( ) ® использованы автонимно.

Выявляем простые высказывания, входящие в состав данного правила, записываем их в естественном языке и обозначаем предложения естественного языка символами ЯЛВ:

А₁: данное буквосочетание является частицей «не» русского языка;

А₂:другое данное буквосочетание является существительным русского языка;

А₃: данное существительное русского языка употребляется в русском языке;

А₄: данная частица «не» в тексте непосредственно предшествует данному существительному русского языка;

В: данная частица «не» написана с данным существительным слитно.

Тогда данное высказывание будет представлено ППФ ЯЛВ: ((А₁ÙА₂) ÙØ А₃) ÙА₄ ® В (скобки опущены в соответствии с соглашением о скобках).

Заменяя нелогические постоянные А₁, А₂, А₃, А₄ и В пропозициональными переменными, получаем пропозициональную форму исходного высказывания: ((p₁Ùp₂) ÙØ p₃) Ùp₄ ® q.

Данная форма в таблице истинности принимает значение л только в одной строке из тридцати двух, а именно, в той строке, в которой антецедент импликации (((p₁Ùp₂) ÙØ p₃) Ùp₄) принимает значение и, а консеквент q – л; следовательно, в этой строке переменным приписываются следующие значения истинности: p₁ – и; p₂ – и; p₃ – л; p₄ – и; q – л. Значит, данное правило будет нарушено только в тех случаях, когда предложения А₁, А₂, А₄ истинные, а А₃, В ложные, то есть: данное буквосочетание является частицей «не» русского языка, другое данное буквосочетание является существительным русского языка, данное существительное русского языка не употребляется в русском языке, данная частица «не» в тексте непосредственно предшествует данному существительному русского языка, а написана данная частица «не» с данным существительным неслитно. В остальных строках пропозициональная форма примет значение и.

Примеры нарушения данного правила: «не вежество», «не ряха» – правило нарушено при таком правописании, так как существительные «вежество», «ряха» не употребляются в современном русском языке, хотя, возможно, употреблялись ранее.

В случае правописания «не счастье» данное правило не нарушено, так как существительное «счастье» употребляется в современном русском языке, и поэтому предложение А₄, подставляемое в пропозициональную форму вместо переменной p₄, является ложным, а, следовательно, переменная p₄ принимает в данном случае значение л, вся конъюнкция ((p₁Ùp₂) ÙØ p₃) Ùp₄ принимает значение л, а вся форма – значение и (так как импликация, антецедент и консеквент которой ложны, истинна).

В случае правописания «несчастье» данное правило вновь не нарушено, так как существительное «счастье» употребляется в современном русском языке; в данном случае импликация истинна, так как ее антецедент ложен, как и в предшествующем случае, а консеквент истинен.

В случае правописания «невежество», «неряха» данное правило не нарушено, так как «вежество», «ряха» не употребляются

в современном русском языке (хотя, возможно, употреблялись ранее), и поэтому вся форма примет значение и, так как и антецедент, и консеквент импликации в данном случае истинны.

2. Предикатная форма

Составим список имен и предикаторов, необходимых для перевода исходного высказывания на ЯЛП1⁼:

имена: нет

атомарные предложения: нет;

предикаторы:

x – буквосочетание А¹(x);

x – частица «не» русского языка В¹(x);

x – существительное русского языка С¹(x);

x употребляется в русском языке 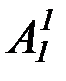(x);

x в тексте непосредственнопредшествует у А²(x,у);

x написана с у слитно В²(x,у).

Заменяем в приведенном выше переводе данного высказывания на ЯЛВ предложения А₁, А₂, А₃, А₄ и В соответствующими предикаторами; получаем пропозициональную форму с индивидными переменными:

((((x – частица «не» русского языка Ù y – существительное русского языка)Ù Øy употребляется в русском языке)Ù x в тексте непосредственнопредшествует у) ® x написана с у слитно),

где: х, у пробегают по буквосочетаниям русского языка.

Запишем составной предикатор на символическом языке:

((((В¹(x)ÙС¹(y))ÙØ 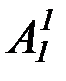(y)) Ù А²(x,у)) ® В²(x,у)).

Исходное высказывание естественного языка утверждает нечто о любых существительных русского языка и любых частицах «не»; поэтому перевод его на ЯЛП1⁼ получается путем связывания всех переменных в сложном предикаторе кванторами общности:

"_А1_(x)"_А1₍_y₎ ((((В¹(x)ÙС¹(y))ÙØ 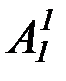(y)) Ù А²(x,у)) ® В²(x,у)).

Для получения предикатной формы заменим в полученном переводе все нелогические (предикатные) константы предикатными переменными:

"_P1₍_x₎"_P1₍_y₎ (((Q¹(x)ÙR¹(y))ÙØ 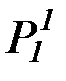(y)) Ù P²(x,у) ® Q²(x,у))

(скобки опущены в соответствии с соглашением о скобках).

Полученное выражение является предикатной формой данного в условии задачи высказывания (вернее, ее сокращенной записью).

Пример 2.17.Найти логическую форму высказывания:

Диагонали данного параллелограмма взаимно перпендикулярны.

1. Пропозициональная форма

Данное высказывание не является теоремой геометрии, то есть представляющая его в языке логики ППФ не является общезначимой (истинной) на универсуме (предметной области) геометрических объектов, но является выполнимой на этом универсуме.

Выявляем простые высказывания, входящие в состав данного высказывания, записываем их в естественном языке и обозначаем предложения естественного языка символами ЯЛВ:

L

четырехугольник KLMN – параллелограмм;

отрезок KM – диагональ KLMN;

отрезок LN – диагональ KLMN;

K M M KM _┴ LN

LN _┴ KM

N

А₁: данная геометрическая фигура KLMN есть параллелограмм;

А₂: данный отрезок KM есть диагональ (данной) геометрической фигуры KLMN;

А₃: данный отрезок LN есть другая диагональ данной геометрической фигуры KLMN;

А₄: данный отрезок KM перпендикулярен другому данному отрезку LN;

А₅: другой данный отрезок LN перпендикулярен данному отрезку KM.

Тогда данное высказывание будет представлено ППФ ЯЛВ: (((А₁ÙА₂) Ù А₃) ÙА₄) ÙА₅ (скобки опущены в соответствии с соглашением о скобках).

Заменяя нелогические постоянные А₁, А₂, А₃, А₄ и А₅пропозициональными переменными, получаем пропозициональную форму исходного высказывания: (((p₁Ùp₂) Ù p₃) Ùp₄) Ùp₅.

Данная форма в таблице истинности принимает значение и только в одной строке из тридцати двух, а именно, в той строке, в которой все переменные принимают значение и, то есть в случае, когда истинны все предложения А₁, А₂, А₃, А₄ и А₅, подставляемые в пропозициональную форму вместо переменных p₁, p₂, p₃, p₄ и p₅соответственно. Таким образом, выполнимость данной пропозициональной формы на предметной области геометрических объектов зависит от существования в этой предметной области объектов, обладающих свойствами и находящихся в отношениях, описываемых предложениями А₁, А₂, А₃, А₄ и А₅. Для выявления этих свойств и отношений необходимо найти предикатную форму данного высказывания.

2. Предикатная форма

Составим список имен и предикаторов, необходимых для перевода исходного высказывания на ЯЛП1⁼:

имена:

данный параллелограмм KLMN а

данный отрезок KM b

другой данныйотрезок LN c

атомарные предложения: нет;

предикаторы:

x – параллелограмм А¹(x);

x – диагональ у А²(x,у);

x перпендикулярен у В²(x,у);

х = у х = у.

Записываем в переводе данного высказывания на ЯЛВ предложения А₁, А₂, А₃, А₄ и А₅ на ЯЛП1⁼:

(((а – параллелограмм Ù b – диагональ а)Ù с – диагональ а)Ù b перпендикулярен с) Ùперпендикулярен b,

(внешние скобки опущены).

Чтобы показать, что b и с – имена разных отрезков, используем запись Ø b = c :

((((а – параллелограмм Ù b – диагональ а)Ù с – диагональ а) ÙØ b = c) Ùb перпендикулярен с) Ù с перпендикулярен b.

Запишем полученное предложение на символическом языке:

((((А¹(a) Ù А²(b,a)) Ù А²(c,a)) Ù Øb = c) ÙВ²(b,c)) ÙВ²(c,b).

Для получения предикатной формы заменим в полученном переводе все нелогические (индивидные и предикатные) константы индивидными и предикатными переменными:

((((P¹(x) Ù P²(y,x)) Ù P²(z,x)) Ù Øy = z) ÙQ²(y,z)) ÙQ²(z,y).

Полученное выражение является предикатной формой данного в условии задачи высказывания (вернее, ее сокращенной записью).

Тема 3. Понятие

Материал данной темы изложен в учебниках из списка литературы: [1], главы 9, 10; [2], главы 6,7; [3], тема 2; [4], главы 5, 6, 7; [5], главы 6, 7; [Доп. лит-ра, 1]; [Доп. лит-ра, 3]; [Доп. лит-ра, 11], главы 2, 4.

Понятиев логике – это мысль о свойствах предметов или отношениях между ними. Свойства предметов и отношения между ними называют в логике признаками предметов. Признаки служат в логике для отличения предметов (упорядоченных совокупностей предметов) или отождествления их. Говорят, что свойстваприсущи или не присущи предметам, предметы находятся или не находятсяв отношении, признаки присущи или не присущи предметам (упорядоченным совокупностям предметов).

В ЯЛФРТ понятия отождествляются с предикатами (пропозициональными функциями) и выражаются предикаторами. Понятия о свойствах предметов (понятия-свойства) отождествляются с одноместными предикатами и выражаются одноместными предикаторами; понятия об отношениях (понятия-отношения) отождествляются с многоместными предикатами и выражаются многоместными предикаторами. Поэтому логические характеристики понятий совпадают в современной логике с логическим характеристиками предикатов. Таким образом, выделяют четыре логические характеристики понятия (предиката).

(1) Предметная областьпонятия: область тех предметов, которым присущи или не присущи свойства, схваченные в данном понятии, или которые находятся или не находятся в отношении, схваченном в понятии. При интерпретации ЯЛФРТ предметная область понятия задается указанием области изменения индивидных переменных, входящих в предикатор, выражающий данное понятие.

(2) Область определения понятия: область определения предиката, отождествляемого с данным понятием. Для понятий-свойств область определения совпадает с предметной областью; область определения понятия-отношения включает кортежи (упорядоченные n-ки) предметов, состоящие из предметов, взятых из областей изменения индивидных переменных в том порядке, в котором эти переменные входят в предикатор, выражающий данное понятие.

(3) Содержание понятия: включает отличительные признаки предметов, то есть те признаки, которые отличают предметы (упорядоченные совокупности предметов) определенного вида от предметов (упорядоченных совокупностей предметов) другого вида; то есть отличительные признаки – это те признаки, которые присущи всем предметам (упорядоченным совокупностям предметов) данного вида. Специфическими называют отличительные признаки, которые присущи только предметам (кортежам предметов) данного вида. Необходимыми называют специфические признаки, отсутствие которых у предмета (кортежа предметов) логически влечет непринадлежность этого предмета (кортежа предметов) к данному виду. Существенными в логике называют необходимые признаки, наличие которых у предмета (кортежа предметов) логически влечет наличие всех остальных необходимых признаков предмета (кортежа предметов).

(4) Объем понятия: множество (класс) предметов (кортежей предметов), обладающих признаками, схваченными в понятии; то есть область истинности предиката, отождествляемого с данным понятием, рассматриваемая как особый абстрактный предмет (см. тему 2, стр. 56-64).

Виды понятий

По предметной области различают конкретные и абстрактные понятия. Предметную область конкретных понятий образуют конкретные предметы, то есть чувственно воспринимаемые (хотя бы в принципе) предметы, существующие в пространстве и времени. Предметную область абстрактных понятий составляют абстрактные предметы, то есть предметы, полученные в результате простой абстракции отождествления или идеализирующих абстракций из конкретных понятий или абстрактных понятий предшествующего уровня абстракции (см. тему 2, стр. 58-60).

По области определения различаются понятия-свойства и понятия-отношения.

По содержанию в классической логике различаются относительные и безотносительные, положительные и отрицательные, собирательные и несобирательные понятия.

Относительными называют понятия-свойства, полученные из понятий-отношений. В современной символической логике предикаты, отождествляемые с относительными понятиями, выражаются одноместными предикаторами, полученными из многоместных предикаторов устранением (элиминированием) всех индивидных переменных, кроме одной, путем подстановки или связывания переменной квантором. Например, понятие, выражаемое предикатором «х – отец Лжедмитрия I» является относительным, так как выражающий его предикатор получен из двухместного предикатора «х отец у» путем подстановки вместо переменной у имени «Лжедмитрий I». Другим примером относительного понятия является понятие «натуральное число, большее пяти», выражаемое предикатором «х >5» (х пробегает по натуральным числам), так как выражающий его предикатор можно рассматривать как полученный из двухместного предикатора «х > у» подстановкой вместо переменной у имени числа 5. Понятие «х – отец» также может быть рассмотрено как относительное понятие, так как предикатор «х – отец» может быть получен из двухместного предикатора «х отец у» путем связывания переменной у квантором существования: «$_у-_{человек}(х отец у)». Безотносительными называют понятия-свойства, которые не могут быть получены из понятий-отношений (например, «х – красный»).

Положительными в логике называют понятия, в содержание которых входят признаки, представленные в ЯЛФРТ предикаторами, не содержащими знака отрицания Ø. В содержание отрицательных понятий входит хотя бы один признак, представленный в ЯЛФРТ предикатором, содержащим знак отрицания Ø. Например, понятие «член парламента, не поддержавший данный законопроект» является отрицательным, так как выражается предикатором «х – член парламента Ù Ø х – поддержавший данный законопроект».

Слова-понятия естественного языка могут использоваться в различных контекстах в разделительном или собирательном смыслах. При использовании слова-понятия в разделительном смысле оно выступает в функции предикатора; в этом случае предметы (или совокупности предметов), характеризуемые данным понятием, рассматриваются как элементы объема данного понятия, то есть элементы множества. В тех контекстах, где слова-понятия естественного языка используются в собирательном смысле, они выступают в функции имени, то есть обозначают единичные предметы (или совокупности предметов), частями которых являются предметы, входящие в объем понятия, выражаемого данным словом-понятием, когда оно используется в разделительном смысле. Например, слова «ученики данного класса» в предложении «Ученики данного класса справились с контрольной по физике» используются в разделительном смысле, то есть выражают понятие «х – ученик данного класса»; данное предложение имеет то же самый смысл, что и предложение «Каждый ученик данного класса справился с контрольной по физике». В предложении «Ученики данного класса провели собрание» слова «ученики данного класса» используются в собирательном смысле, то есть выступают в функции имени конкретного предмета – данного коллектива, состоящего как целое из отдельных учеников; поэтому смысл данного предложения не совпадает со смыслом предложения «Каждый ученик данного класса провел собрание». В традиционной логике такое различие в использовании слов-понятий характеризовали с помощью терминов «собирательные понятия» и «несобирательные понятия», то есть под собирательными понятиями в традиционной логике понимают использование слов-понятий в собирательном смысле, а под несобирательными понятиями – использование слов-понятий в разделительном смысле.

По объему различают нулевые, единичные, общие и универсальные. Нулевыми называются понятия, объем которых не содержит ни одного элемента из области определения понятия. Объем нулевого понятия называется пустым множеством и обозначается знаком Æ. Объем единичного понятия содержит один единственный элемент из области определения понятия. Общими называют понятия, объемы которых содержат более одного элемента, но не содержат все элементы из области определения понятия. Объем универсального понятия включает все элементы области его определения и обозначается знаком 1.