Общие семантические правила ЯЛФРТ
Построение семантики неинтерпретированного формального языка логикиначинается с задания его интерпретации.
Интерпретация некоторого неинтерпретированного формального ЯЛФРТ предполагает следующие действия.
(1) Всему ЯЛФРТ сопоставляется универсум рассуждения (область интерпретации), то есть некоторая однозначно определенная предметная область, состоящая из единичных индивидуальных предметов (индивидов). Область интепретации любого ЯЛФРТ включает в себя подобласть, содержащую два абстрактных предмета: истину и ложь; в дальнейшем эта подобласть будет обозначаться {и, л}.
(2) Каждой именной константе ставится в однозначное соответствие предмет из области интерпретации.
(3) Каждой именной переменной ставится в однозначное соответствие область ее изменения (подобласть области интерпретации), то есть область, включающая предметы, имена которых подставляются вместо данной переменной.
(4) Каждой пропозициональной константе ставится в однозначное соответствие один из двух абстрактных предметов: истина или ложь.
(5) Каждой пропозициональной переменной ставится в однозначное соответствие область {и, л}.
Таким образом, интерпретация задает денотаты, то есть предметные значения, или области изменения атомарным выражениям ЯЛФРТ, то есть ППТ и ППФ, содержащим в своем составе только один символ, что фиксируется семантическим правилами ПС.1. и ПС.2.
ПС.1. (Правило семантическое первое). Именная (предметная, индивидная) константа в заданнойинтерпретации ЯЛФРТ обозначает (именует, называет) единичный предмет из области интерпретации ЯЛФРТ; именная (предметная, индивидная) переменная в заданной интерпретации принимает значения в (пробегает по) области своего изменения.
ПС.2. (Правило семантическое второе). Пропозициональная константа в заданнойинтерпретации ЯЛФРТ обозначает (именует, называет) один из двух абстрактных предметов – истину или ложь; И обозначает абстрактный предмет и (истину), а Л – л (ложь) в любой интерпретации ЯЛФРТ. Пропозициональная переменная в любой интерпретации ЯЛФРТ принимает значения в (пробегает по) предметной области {и, л}.
Схема 2.4
с р А И
х у z В
авЛ
И
Л
Вторым важнейшим семантическим понятием языков логики является понятие функции.
Под функцией в логике понимают много-однозначное или одно-однозначное соответствие между двумя областями, первая из которых называется областью определения функции (ОО), а вторая – областью значений функции (ОЗ). Область определения функции состоит из элементов: предметов или упорядоченных n-ок предметов (n=2,3,4, …), называемых также кортежами или n-членными последовательностями; в первом случае функция называется одноместной или одноаргументной, а во втором – n-местной или n-аргументной (n=2,3,4, …). Функция каждому элементу из ОО ставит в соответствие один и только один предмет из ОЗ, но при много-однозначном соответствии различным элементам из ОО может ставиться в соответствие одини тот же предмет из ОЗ, а при одно-однозначном соответствии различным элементам из ОО ставятся в соответствие различные предметы из ОЗ. Область значений функции в обоих случаях включает в себя предметы. Если не всем элементам из ОО ставятся в соответствие предметы из ОЗ, то такое соответствие называется частичной функцией (из ОО в ОЗ). Упорядоченную n-ку предметов (n=2,3,4, …) мы будем обозначать с помощью угловых скобок: áа1, а2, …,аnñ – упорядоченная n-ка (n-членный кортеж) предметов, называемых именами а1, а2, …,аn . Две упорядоченные n-ки предметов áа1, а2, …,аnñ и áb1, b2, …,bmñ равны друг другу (представляют собой одну и ту же упорядоченную n-ку предметов): áа1, а2, …,аnñ = áb1, b2, …,bmñ, если и только если: (1) n=m; (2) аi и bi называют один и тот же предмет, что выражается с помощью знака логического равенства: ai=bi(1£i £ n).
Говорят, что функция определена на данной предметной области, если и только если ее область определения содержит предметы из данной предметной области или упорядоченные n-ки предметов из данной предметной области.
Введенное здесь понятие функции позволяет сформулировать семантические правила, приписывающие смысловые значения выражениям ЯЛФРТ, относящимся к семантической категории функторов (то есть включающим в свой состав переменные). При интерпретации ЯЛФРТ функции, определенные на области интерпретации, сопоставляются функторам данного ЯЛФРТ (то есть выражениям, содержащим в своем составе переменные) как их смысловые значения.
ПС.3. (Правило семантическое третье). Функтор выражает функцию.
Пример 2.4. Функтор «отец …» (пустое место замещается именами людей) выражает функцию:
ОО (область определения) ОЗ (область значений)
люди за весь период их жизнилюди за весь период их жизни
а а
Елизавета Петровна · ·
Романова
b b
Алексей Михайлович · ·
Романов
cc
Петр I · ·
a1 a1
Михаил Романов · ·
Согласно определению, функция ставит в соответствие каждому человеку из ОО другого человека из ОЗ – его отца, причем каждому человеку из ОО ставится в соответствие один и только один человек (его отец) из ОЗ, и нескольким людям из ОО может быть поставлен в соответствие один и тот же человек из ОЗ, но не наоборот (много-однозначное соответствие).
При интерпретации операторным и предикатным константам, а также символам коннекторов сопоставляются функции, определенные на универсуме рассуждения (области интерпретации), а для операторных и предикатных переменных указываются области их изменения – то есть области, содержащие функции, определенные на области интерпретации.
ПС.3.1. Элементарный постоянный оператор,содержащий единственную n-местную операторную константу (n=1,2,3, ...), в заданнойинтерпретации выражаетоперацию, то есть функцию, областью определения (ОО) которой является подобластьобласти интерпретации, не содержащая {и, л}, – при n=1; или область, состоящая из упорядоченных n-ок (n-членных последовательностей, кортежей) предметов из этой подобласти, – при n=2,3, ...; а областью значений (ОЗ) – та же самая или другая подобластьобласти интерпретации, не содержащая {и, л}. Элементарный переменный оператор,содержащий n-местную операторную переменную, принимает значения в (пробегает по) области n-местных операций, определенных на области интерпретации.
Элементарный постоянный операторотец1(х) (операторная константа отец1 интерпретируется как операция, выражаемая оператором «отец …»из примера 2.4, х пробегает по области людей) выражает операцию, описанную в примере 2.4.
Пример 2.5.Оператор +2(х,у) (+2 интерпретируется как «… + ***»; x, у пробегают по области натуральных чисел) выражает двуместную операцию сложения натуральных чисел, то есть функцию:
ОО ОЗ
упорядоченные двойки натуральные числа
натуральных чисел
á1,2ñ · · 3
á2,7ñ ·
á3,5ñ · · 8
á5,3ñ · · 9
ПС.3.2. Элементарный n-местныйпостоянный предикатор в заданной интерпретациивыражает n-местныйпредикат (пропозициональную функцию), то есть функцию, ОО которой является подобласть области интерпретации, не содержащая {и, л}, – при n=1, или область, состоящая из упорядоченных n-ок (n-членных последовательностей, кортежей) предметов из этой подобласти, – при n=2,3, ..., а ОЗ – {и, л}. Элементарный n-местныйпеременный предикатор пробегает по (принимает значение в) области n-местных предикатов, определенных на области интерпретации.
Пример 2.6.Предикатор А1(х) (А1интерпретируется как «…(есть) отец»; x пробегает по области людей, то есть по той же области, что и в примере 2.4) выражает предикат:
ОО ОЗ
люди {и, л}
а
Елизавета Петровна ·
Романова
b и
Алексей Михайлович · ·
Романов л
c·
Петр I ·
a1
Михаил Романов ·
Пример 2.7. Предикатор А2(х,у) (А2интерпретируется как «…(есть) отец * * *»; x, у пробегают по области людей, то есть по той же области, что и в примерах 2.4, 2.6 ) выражает предикат:
ОО ОЗ
упорядоченные пары людей {и, л}
áс, аñ ·
áа, сñ · · и
áс, bñ · ·л
áa, bñ ·
áa, añ ·
В современной логике вводится понятие 0-местного функтора и 0-местной функции. 0-местная функциональная константа обозначает предмет из универсума рассуждений; 0-местная функциональная переменная совпадает с индивидной переменной. 0-местная предикатная константа совпадает с пропозициональной константой, 0-местный предикат оказывается одним из двух абстрактных предметов – и или л; 0-местная предикатная переменная совпадает с пропозициональной переменной.
Каждый предикат разбивает область своего определения на две области: область истинности предиката, то есть область, состоящую из тех элементов ОО предиката, которым предикат ставит в соответствие и, и область ложности предиката, то есть область, состоящую из тех элементов ОО предиката, которым предикат ставит в соответствие л.
Предикаты в современной логике отождествляются с понятиями в традиционной логике, то есть с мыслями о свойствах предметов и отношениях между ними (с мыслями о признаках предметов). Понятия-свойства отождествляются с одноместными предикатами и выражаются одноместными предикаторами, а понятия-отношения отождествляются с многоместными предикатами и выражаются многоместными предикаторами.
Графический язык представления предикатов
ОО предиката изображается прямоугольником, каждая точка которого представляет элемент (предмет или кортеж предметов) ОО предиката, а область истинности предиката изображается кругом, внутренние точки которого представляют элементы, которым предикат ставит в соответствие и.
Предикаты из примеров 2.6. и 2.7. графически представляются следующим образом:
«x (есть) отец» : А1(x) «x (есть) отец y»: А2(x, y)
ОО: люди ОО: упорядоченные
пары людей
| А1 |
| А2 |
Область истинности предиката [, выражаемого предикатором] Аn(x1, x2 ,…,xn)[,] обозначается на схеме символом Аn без переменных (n=1,2,3, ...). Здесь символы Аn, x1, x2 ,…,xn являются символами метаязыка; Аn – метапеременная, пробегающая по n-местным предикатным константам языка-объекта, x1, x2 ,…,xn – метапеременные, пробегающие по индивидным переменным символам языка-объекта; скобки, запятые, многоточие использованы автонимно.
Записанные в квадратных скобках выражения в дальнейшем мы будем опускать, то есть вместо полной записи «предикат, выражаемый предикатором Аn(x1, x2 ,…,xn)», мы будем использовать сокращенную запись «предикат Аn(x1,x2 ,…,xn )».
ПС.3.3. Элементарный коннектор в каждой интерпретации выражает n-местную истинностную функцию (n=1, 2), то есть функцию, ОО которой является {и, л} (при n=1) или двучленные кортежи предметов из {и, л} (при n=2), а ОЗ – {и, л}.
Область определения n-местной истинностной функции состоит из 2n элементов; поэтому истинностные функции задаются с помощью таблиц.
Коннектор (Øp) выражает истинностную функцию, задаваемую таблицей 2.3.
Таблица 2.3
| p | (Øp) |
| и | л |
| л | и |
Дизъюнкция в современной логике выражает две истинностные функции: одна называется нестрогой (неисключающей) дизъюнкцией и выражается знаком Ú, а другая называется строгой (исключающей) дизъюнкцией и выражается знаком Ú (или знаком Ú с каким-нибудь другим дополнением).
Элементарные коннекторы (pÚq) (дизъюнкция неисключающая), (pÚq) (дизъюнкция исключающая), (p«q) (эквиваленция), (p®q) (импликация) выражают истинностные функции, задаваемые таблицей (внешние скобки в записи ППФ в дальнейшем опускаются):
Таблица 2.4
| p | q | pÙq | pÚq | pÚq | p®q | p«q |
| и | и | и | и | л | и | и |
| и | л | л | и | и | л | л |
| л | и | л | и | и | и | л |
| л | л | л | л | л | и | и |
При переводе выражений естественного языка на ЯЛФРТ следует постоянно иметь в виду различие семантики предложений естественного языка и ЯЛФРТ, а именно: повествовательное предложение естественного языка обозначает положение дел (ситуацию) в некоторой предметной области, а предложение ЯЛФРТ обозначает один из двух абстрактных предметов: иили л. Поэтому семантика грамматических союзов «... и ...», «... или ...», «если ..., то», «неверно, что ...» в естественном языке не совпадает с семантикой коннекторов ЯЛФРТ, которые выражают связи лишь между истинностными значениями предложений, а не между обозначаемыми ими (в естественном языке) положениями дел. Например, такие предложения естественного языка, как (1) «Число 18 делится на 9 без остатка и число 27 делится на 9 без остатка», (2) «Число 18 делится на 9 без остатка, а число 12 не делится на 9 без остатка», (3) «Если число 18 делится на 9 без остатка, то число 12 не делится на 9 без остатка» будут записаны в ЯЛФРТ с помощью конъюнкции: (1) АÙВ, (2) АÙØ С, (3) АÙØС, где А интерпретируется как предложение «Число 18 делится на 9 без остатка»; В – как «Число 27 делится на 9 без остатка»; С – как «Число 12 делится на 9 без остатка». Предложения (1), (2), (3) естественного языка содержат разные грамматические союзы, поскольку предложением (1) утверждается одинаковость, сходство, подобие ситуаций, обозначаемых составляющими его простыми предложениями, а предложениями (2) и (3) утверждается противоположность этих ситуаций. При переводе этих предложений на ЯЛФРТ существенным оказывается то обстоятельство, что каждое из этих трех сложных предложений истинно если и только если истинны составляющие их предложения, что как раз и выражается логическим союзом конъюнкцией.
Таким образом, в естественном языке конъюнкция может быть представлена грамматическими союзами «... и ...», «..., а ...», «если ..., то ...» или знаками препинания («Дело под вечер. Зимой»). Отметим также, что бессмысленные с точки зрения семантики естественных языков предложения (например, «В огороде бузина, а в Киеве дядька») при переводе на ЯЛФРТ становятся осмысленными конъюнктивными предложениями.
Дизъюнкция (исключающая и неисключающая) представлена в естественном языке союзами «... или ...», «или ..., или ...», «... и ...» («Доктора наук и доценты могут участвовать в конкурсе на замещение должности заведующего кафедрой»), или знаками препинания. О какой дизъюнкции (строгой или нестрогой) идет речь в предложении естественного языка, выясняется из контекста.
Тот смысл, который выражается импликацией ЯЛФРТ, в традиционной логике называется «материальной импликацией» (Аристотель). Материальная импликация фиксирует лишь один из многочисленных смыслов союза «если ..., то ...» в естественном языке. Чаще всего «если ..., то ...» естественного языка выражает причинно-следственную связь или связь основание-следствие между положениями дел, обозначаемыми предложениями естественного языка; поэтому при переводе предложений естественного языка на ЯЛФРТ возникают «парадоксы материальной импликации».
I парадокс: Предложение «Если 2х2=4, то Наполеон – император», бессмысленное в естественном языке, является осмысленным в ЯЛФРТ и даже истинным (так как истинны оба члена импликативного предложения).
II парадокс: Предложение «Если 2х2=5, то Наполеон – император», бессмысленное в естественном языке, также является истинным в ЯЛФРТ (третья строка таблицы 2.4 для импликации).
III парадокс: Предложение «Если 2х2=5, то Наполеон – Герой России», бессмысленное в естественном языке, также является истинным в ЯЛФРТ (четвертая строка таблицы 2.4 для импликации).
Смысл союза «если ..., то ***», фиксируемый материальной импликацией, лучше всего передается конструкцией «неверно, что (... и не ***)».
Конъюнкция, дизъюнкция (строгая и нестрогая) и эквиваленция являются симметричными логическими союзами, то есть истинностное значение сложного предложения, образованного с помощью этих союзов, не меняется при перемене мест составляющих предложений. Импликация не является симметричным коннектором; первый член импликации обычно называют антецедентом (от латинского antecedens – предшествующий), а второй – консеквентом (от латинского consequius – последующий). Антецедент импликации называют также достаточным условием (для консеквента), а консеквент – необxодимым условием (для антецедента). Предложение ЯЛФРТ А®В может быть представлено одной из конструкций естественного языка: (1) «если А, то В»; (2) «В, если А»; (3) «А достаточно для того, чтобы В»; (4) «В необходимо для того, чтобы А». Слово «только», поставленное перед словом «если» в предложении естественного языка, равнозначно по смыслу перемене мест членов импликации. Например, предложение «Если Алик за рулем, то мы едем с превышением скорости» запишется в ЯЛФРТ формулой «А®В», где А представляет предложение «Алик за рулем», а В – «Мы едем с превышением скорости», в то время как предложение «Только если Алик за рулем, то мы едем с превышением скорости» запишется в ЯЛФРТ формулой «В®А».
Кроме указанных способов выражения, материальная импликация может быть представлена в естественном языке словами «следовательно», «значит», «поэтому», «потому что», «так как».
Наличие у грамматического союза естественного языка «если ..., то ...» смысла, выражаемого материальной импликацией, можно проиллюстрировать следующим примером.
Пример 2.8. Предложение «Если число а делится без остатка на 4, то оно делится без остатка на 2» является истинным в арифметике натуральных чисел, то есть оно должно быть истинным для любого натурального числа.
1 случай. Пусть мы взяли число а=12, тогда предложение «Число 12 делится без остатка на 4» будет истинно и предложение «Число 12 делится без остатка на 2» тоже истинно; это соответствует первой строке в таблице 2.4. для импликации.
2 случай. Пусть мы взяли число а=10. Тогда антецедент импликации будет ложным, консеквент истинным, а все предложение истинным, что соответствует третьей строке в таблице 2.4. для импликации.
3 случай. Пусть мы взяли число а=11. Тогда и антецедент, и консеквент импликации будут ложными, а все предложение –
истинным, что соответствует четвертой строке в таблице 2.4 для импликации.
Какое бы число мы ни взяли, мы никогда не получим случай, когда антецедент импликации будет истинным, а консеквент ложным. Значит смысл данного предложения можно передать словами: «Не может быть, что (неверно, что) число делится на 4 без остатка ине делится на 2 без остатка».
Эквиваленция представляется в естественном языке словами «... если и только если ...», «... тогда и только тогда, когда ...», «...необходимо и достаточно для того, чтобы ...» и т.д.
Составными коннекторами будем называть составные коннекторные ППФ, содержащие, кроме символов коннекторов, только пропозициональные переменные.
Истинностные функции, выражаемые составными коннекторами, представляются таблицами, в которых сопоставление значений и и л наборам значений переменных осуществляется последовательно, по строению ППФ.
Пример 2.9.Неэлементарный составной коннектор pÙq®r (скобки опущены в соответствии с соглашением о скобках) выражает истинностную функцию, задаваемую следующей таблицей.
| p | q | r | pÙq | pÙq®r | |
| и | и | и | и | и | |
| и | и | л | и | л | |
| и | л | и | л | и | |
| л | и | и | л | и | |
| и | л | л | л | и | |
| л | и | л | л | и | |
| л | л | и | л | и | |
| л | л | л | л | и | . |
Истинностные функции могут выражаться не только правильно построенными формулами языка-объекта, но и выражениями метаязыка. Так, например, всякая ППФ вида AÙВ®C (скобки опущены в соответствии с соглашением о скобках) выражает ту же самую истинностную функцию, что и ППФ pÙq®r:
| А | В | С | АÙВ | АÙВ®С | |
| и | и | и | и | и | |
| и | и | л | и | л | |
| и | л | и | л | и | |
| л | и | и | л | и | |
| и | л | л | л | и | |
| л | и | л | л | и | |
| л | л | и | л | и | |
| л | л | л | л | и | . |
В нижеследующих семантических правилах для кванторных выражений ПС.3.4."иПС.3.5.$символ А1 – метапеременная по одноместным предикатным константам, х – метапеременная по индивидным переменным, В(х) – метапеременная по ППФ, содержащим индивидную переменную х в качестве единственной свободной переменной, символы кванторов и скобки использованы автонимно. Согласно ФИО ППФ В(х) является одноместным предикатором (элементарным или составным).
ПС.3.4.". Предложение "А1(x)В(x)истинно, если и только если предикат [, выражаемый предикатором] В (x) ставит в соответствие значение ивсем тем предметам из области своего определения, которым ставит в соответствие значение и предикат [, выражаемый предикатором] А1(x).
В дальнейшем выражения в квадратных скобках будут опускаться.
ПС.3.5.$.Предложение $А1(x)В (x)истинно, если и только если предикат В(x) ставит в соответствие значение ихотя бы одному предмету из области своего определения, которому ставит в соответствие значение и предикат А1(x).
В классической логике кванторные выражения считаются осмысленными при выполнении следующих условий:
(1) предикаты А1(x) и В(x) имеют общую область определения (то есть общую предметную область);
(2) область истинности предикатов А1(x) и В(x) не пуста и не совпадает с их ПрО.
При выполнении этих условий значение истинности кванторного предложения определяется отношением областей истинности предикатов, выражаемых ППФ А1(x) и В(x), что демонстрируется схемой 2.5.
Схема 2.5
| В |
| А1 В |
| А1 |
$А1(x)В(x) и$А1(x)В(x) и
3случай: 4 случай:
| В |
| А1 |
| В |
| А1 |
$А1(x)В(x) л $А1(x)В(x) и
| А1 |
5 случай:
| В |
$А1(x)В(x) и
.
Правила ПС.3.1–ПС.3.3, ПС.3.4.", ПС.3.5.$ задают смыслы функторов ЯЛФРТ. Каковы предметные значения (денотаты) этих функторов? В некоторых случаях функции, выражаемые функторами, рассматриваются как абстрактные предметы, обозначаемые этими функторами; однако в большинстве ЯЛФРТ функторы рассматриваются как выражения, не имеющие денотатов; такие выражения называются синкатегорематическими, в отличие от категорематическиx выражений, то есть выражений, имеющих не только смысловое, но и предметное значение.
Абстрактор– это сложный функтор ЯЛФРТ, переводящий путем связывания пустого места предикатор (оператор) в имя абстрактного предмета, полученного из предиката (операции), выражаемого этим предикатором (оператором), с помощью особого логического действия – абстракции. В естественном языке абстрактор выражается словами: «свойство», «отношение», «признак» и т.д., например, выражение естественного языка «свойство быть красным» («краснота») представляется в ЯЛФРТ как результат действия абстрактора «свойство …, такое что [+++]» на предикатор «… (есть) красный». Выражение ЯЛФРТ «свойство …, такое что [… (есть) красный]» является именем абстрактного предмета – красноты; вхождение пустого места «…» в это выражение является связанным.
Классообразователь (функтор множества) – сложный функтор ЯЛФРТ, переводящий путем связывания пустого места предикатор в имя абстрактного предмета – класса или множества. В естественном языке классообразователь выражается словами «множество» или «класс». Выражение естественного языка «множество людей» в ЯЛФРТ представляется как результат действия классообразователя «множество (класс) … таких что [+++]» на предикатор «… (есть) человек». Выражение ЯЛФРТ «множество (класс) …, такое что [… (есть) человек]» является именем абстрактного предмета – множества (класса) людей.
Для того, чтобы определить смыслы абстрактора и классообразователя, необходимо ввести в рассмотрение особое логическое действие – абстракцию. Под абстракцией в логике понимают логическое действие, при котором некоторая функция (предикат, операция) рассматривается как особый предмет – абстрактный предмет. Дело в том, что в семантике ЯЛФРТ имеют дело с двумя видами «сущностей»: предметами, то есть денотатами имен, и функциями, то есть смыслами функторов. Предметы в общем случае не являются функциями, а функции не являются предметами. Абстракция в логике как раз и понимается как переход к новой предметной области, предметами которой являются функции, определенные на исходной предметной области. Абстрактор и классообразователь входят в состав правильно построенных термов ЯЛФРТ. Фундаментальное индуктивное определение ППТ дополняется теперь новым пунктом:
(4i) (индукционный шаг) если Fn – n-местная операторная (функциональная) константа, Аn – n-местная предикатная константа, x, x1, x2, … xn – индивидные переменные (n=1,2,…), l – знак абстрактора, {½ } – знак классообразователя, то выражения вида: lxФ1(x), lxА1(x), lx1,x2,...,xnФn(x1, x2 ,…,xn), lx1,x2,...,xnАn(x1, x2 ,…,xn), {x½А1(x)}, {áx1, x2, ..., xnñ½Аn(x1, x2, ..., xn)} – ППТ (символы абстрактора, классообразователя, скобки, запятые употреблены автонимно).
Смыслы ППТ и ППФ, содержащих символ абстрактора, задается следующим семантическим правилом.
ПС3.6. (i) Выражение lxФ1(x) обозначает одноместную операцию, определенную на области изменения переменной х, рассматриваемую как особый абстрактный предмет, то есть предмет, полученный из функции (операции) с помощью логического действия абстракции.
(ii) Выражение lx1,x2,...,xnФn(x1, x2 ,…,xn) обозначает n-местную операцию, определенную на области упорядоченных n-ок предметов, взятых из областей изменения переменных x1, x2,…,xn в соответствующем порядке, рассматриваемую как особый абстрактный предмет.
(iii) Выражение lxA1(x) обозначает одноместный предикат, определенный на области изменения переменной х, рассматриваемый как особый абстрактный предмет.
(iv) Выражение lx1,x2,...,xnАn(x1, x2 ,…,xn) обозначает n-местный предикат, определенный на области упорядоченных n-ок предметов, взятых из областей изменения переменных x1, x2,…,xn в соответствующем порядке, рассматриваемый как особый абстрактный предмет.
Пример 2.10.На предметной области конкретныx предметов (то есть предметов, доступных чувственному восприятию, существующих в пространстве и времени) определяются конкретные предикаты: «x –красный», «x – синий», «x – зеленый», «x – твердый», «x – горький».
ОО: конкретные предметы
| |
| В1 |
| А1 |
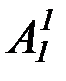 (x)
(x)
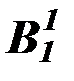
|
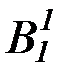 (x)
(x)
ОО:свойства конкретных предметов x – цвет А1(x)
| А1 · · ·· . |
. .
lx(x – красный) lx(x – синий)
Действуя абстрактором lx(...) на предикаторы А1(x) – 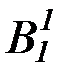 (x), получаем имена предметов новой предметной области – области абстрактных предметов, предметами которой являются свойства конкретных предметов, рассматриваемые как особые предметы: lx(x –красный) – «свойство быть красным», «краснота»;lx(x –синий) – «синева»; lx(x –твердый) – «твердость»; lx(x –горький) – «горечь». На новой предметной области абстрактных предметов определяются новые предикаты – абстрактные предикаты (абстрактные понятия), например, предикат «x – цвет».
(x), получаем имена предметов новой предметной области – области абстрактных предметов, предметами которой являются свойства конкретных предметов, рассматриваемые как особые предметы: lx(x –красный) – «свойство быть красным», «краснота»;lx(x –синий) – «синева»; lx(x –твердый) – «твердость»; lx(x –горький) – «горечь». На новой предметной области абстрактных предметов определяются новые предикаты – абстрактные предикаты (абстрактные понятия), например, предикат «x – цвет».
Терминология любой науки, использующей аппарат современной логики, содержит термины (понятия) различных уровней абстракции. Уровень абстракции научной терминологии определяется индуктивно:
1) 0-ой (нулевой) уровень абстракции (уровень абстракции с порядковым номером 0) составляют конкретные предикаты (понятия);
2) n+1-ый (n плюс первый) уровень абстракции (уровень абстракции с порядковым номером n+1) составляют понятия (предикаты), область определения которых состоит из абстрактных предметов, полученных путем абстракции из понятий n-ого уровня абстракции, или кортежей этих абстрактных предметов;
3) каждый термин научной терминологии относится к одному и только одному уровню абстракции.
Определенное выше логическое действие называется также абстракцией отождествления, поскольку в основе этого действия лежит отождествление предметов (или кортежей предметов) по общему для них свойству (отношению). При образовании абстрактных предметов в науках, использующих аппарат современной логики, применяют также так называемые идеализирующие абстракции; с помощью таких абстракций вводятся так называемые идеальные или идеализированные объекты, то есть объекты, фиксирующие свойства, заведомо отсутствующие у конкретных объектов («идеальный газ», «идеальная паровая машина» и т. д.). Наиболее употребительными в математике являются абстракция потенциальной осуществимости, с помощью которой образуется потенциально бесконечный ряд натуральных чисел (мы отвлекаемся здесь от ограниченности материальных возможностей построения конкретных совокупностей материальных предметов, содержащих любое число членов), и абстракция абсолютной осуществимости, согласно которой в логике признается существующим любой абстрактный предмет с непротиворечивыми свойствами; с помощью данной абстракции в математике при рассуждениях о потенциально бесконечных последовательностях используются в полном объеме законы классической логики (в частности, законы непротиворечия и исключенного третьего), что равнозначно рассмотрению таких принципиально незавершенных конструкций как законченных, данных всеми своими членами одновременно.
С понятием абстракции тесно связан важнейший принцип дидактики – принцип наглядности обучения. В отношении терминологии изучаемой научной дисциплины суть этого принципа может быть выражена следующим образом:в процессе преподавания любой научной дисциплины все термины должны вводится последовательно, начиная с нулево
Дата добавления: 2021-01-26; просмотров: 643;











