Язык логики высказываний (ЯЛВ)

Алфавит ЯЛВ:

(1) А, В, С, А₁, В₁, ..., И, Л –пропозициональные константы;

(2) р, q, r, p₁ ,q₁ , … – пропозициональные переменные;

(3) Ø, Ù, Ú, Ú,®, « – логические постоянные;

(4) ( ) , – технические знаки.

(1) и (2) называются собственными символами.

ППФ (правильно построенная формула) ЯЛВ:

(1) отдельно стоящая пропозициональная константа есть ППФ;

(2) отдельно стоящая пропозициональная переменная есть ППФ;

(3) если А и В – ППФ, то:

(ØА), (АÙВ), (АÚВ), (А Ú В), (А®В), (А«В) – ППФ;

(4) ничто иное не есть ППФ ЯЛВ.

Например, р есть ППФ; q есть ППФ; (Øр) – ППФ; ((Øр)®(pÙ(q®(Øр)))) – ППФ; (А®p) –ППФ; ((АÚp)®И) –ППФ и т.д.

ППФ, не содержащая пропозициональных переменных, называется замкнутой ППФ (предложением).

Языки логики с точно заданным синтаксисом, то есть с точно заданным алфавитом и с понятиями терма и ППФ, заданными с помощью фундаментальных индуктивных определений, называют часто исчислениями.

Язык чистого исчисления высказываний не содержит пропозициональных констант.

Язык логики предикатов первого порядка с равенством (ЯЛП1⁼)

АлфавитЯЛП1⁼:

(1) пропозициональные константы;

(2) пропозициональные переменные;

(3) индивидные константы;

(4) индивидные переменные;

(5) предикатные константы;

(6) предикатные переменные;

(7) логические постоянные: (а) Ø, Ù, Ú, ®, «;

(б) ", $ – кванторы;

(в) =;

(8) ( ) ,– технические знаки.

Алфавит ЯЛП1⁼ содержит новый символ – символ равенства =, являющийся двухместной предикатной константой.

Понятие ППТ ЯЛП1⁼ совпадает с понятием ППТ, данным выше (см. стр. 37-38).

В прикладных исчислениях предикатов первого порядка есть термы, образованные с помощью функциональных (операторных) символов; в чистом исчислении предикатов первого порядка (с равенством) отсутствуют термы, включающие операторные символы.

Понятие ППФ ЯЛП1⁼ задается фундаментальным индуктивным определением ППФ, данным выше (см. стр. 40), к которому добавляется еще один индукционный шаг:

Язык исчисления предикатов первого порядка ЯЛП1 отличается от ЯЛП1⁼ тем, что (1) в алфавите ЯЛП1 отсутствует пункт (7) (в), то есть знак =; (2) в определении ППФ отсутствует пункт (5а).

Вхождение переменной х в ППФ называется связанным, если и только если х находится в области действия квантора по переменной х. В противном случае вхождение х называется свободным.

В ЯЛП1⁼ избегают использования одних и тех же индивидных переменных для обозначения связанных и свободных вхождений переменных (во избежание коллизий). Разграничение связанных и свободных переменных вводится двумя путями:

(1) вводят отдельные обозначения для связанных переменных: свободные переменные обозначаются w, v, u, w₁, …; связанные переменные – x, y, z, x₁, …;

(2) переменная переименовывается, если она встречается в контексте и как связанная, и как свободная, например (("_х P¹(x))®Q¹(x))=*(("_х P¹(x))®Q¹(y)) (=* означает, что правая и левая по отношению к знаку =* части записи тождественны по смыслу; читается: «графически равно»).

В определении ППФ ЯЛП1⁼ используются неограниченные кванторы, то есть выражения вида: "_х А, $_х В, "_х (pÙq), "_х А(x), $_х В(x), "_х А(x,y), $_х В(x,y), "_х P²(x,y), где:

x, y – синтаксические метапеременные по индивидным переменным языка-объекта;

p, q – синтаксические метапеременные по пропозициональным переменным языка-объекта;

A, B – синтаксические метапеременные по ППФ;

A(х), B(х), A(х,у), B(х,у)– синтаксические метапеременные по ППФ,содержащим свободные вхождения только х или х и у;

P² – синтаксическая метапеременная по предикатным переменным;

знаки кванторов и коннекторов, скобки, запятые использованы автонимно.

Выражения с неограниченными кванторами связаны с ограниченными кванторами соотношениями:

"_А1_(x)B(x)=* "_x(А¹(x)®B(x))

$_А1_(x)B(x)=* $_x(А¹(x)ÙB(x)).

ППФ вида: "_хА, $_хВ, где А и В – ППФ, не содержащие свободных вхождений переменной х, имеют тот же смысл, что А и В соответственно.

ППФ вида "_хА²(x,y) выражает одноместный предикат, который ставит в соответствие значение истинно тем предметам из области изменения переменной у, которые встречаются в области истинности предикатаА²(x,y)в паре с любым предметом из области изменения переменной х.

В ЯЛП1 используются только кванторы, связывающие индивидные переменные. В исчислении предикатов более высокого порядка в качестве квантифицируемых переменных используются предикатные переменные.

Семантика ЯЛП1^=*

До сих пор определялись предметные значения и смыслы атомарных и элементарных ППТ и ППФ языка логики. Для завершения построения семантической теории ЯЛФРТ необходимо указать способы сопоставления семантической оценки составным выражениям языка логики.

В современной логической семантике исходным понятием для введения понятия истинной формулы является семантический предикат «последовательность приписывания значений переменным j выполняет ППФ А в полумодели (реляционной системе) áU, Jñ».

Построение семантической теории языка логики предикатов первого порядка начинается с указания реляционной системыили полумодели.

Реляционной системойили полумодельюM=*áU, Jñназывается упорядоченная пара, состоящая из непустого множества объектовU, называемого областью интерпретацииили универсумом рассуждения, и семантической функции J, называемой интерпретационной функцией(или интерпретацией), определенной на множестве нелогическихконстантязыка логики предикатов первого порядка. Интерпретационная функция сопоставляет:

(1) каждой пропозициональной константе – один из двух абстрактных предметов: истину (и) или ложь (л);

(2) каждой индивидной константе ЯЛП1⁼ – предмет из множества U;

(3) каждой n–местной функциональной константе (для языка прикладного исчисления предикатов первого порядка) – n-местную операцию, сопоставляющую упорядоченным n-кам предметов из множества U предметы из того же множества U;

(4) каждой n-местной предикатной константе – n-местныйпредикат (пропозициональную функцию), определенный на n-членных кортежах (упорядоченных n-ках) предметов из U.Согласно тезису экстенсиональности,n-местный предикат отождествляется с областью его истинности, т.е. в стандартной теоретико-множественной семантикеn-местный предикат рассматривается как множествоупорядоченных n-ок (n-членных кортежей) предметов из U (тех самых, которым соответствующий предикат ставит в соответствие значение истинно).

Таким образом, интерпретационная функция Jставит в соответствие:

(1) каждому терму t, содержащему толькоименные и функциональные константы, определенный предмет из области интерпретации;

(2) каждому терму t(x₁, x₂,…, x_n), содержащему n индивидных переменных и не содержащему функциональных переменных – определенную n-местную операцию на области интерпретации U;

(3) каждому терму Фⁿ( 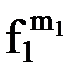( 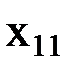, ,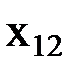…, 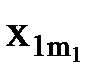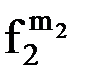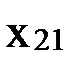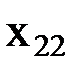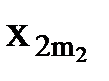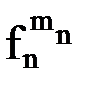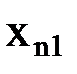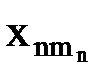), ( , , …, ), …, ( , , …, )), содержащему n-местную функциональную константуФⁿ, n функциональных переменных (i=1, 2, …, n) и k индивидных переменных (k –общее число различных переменных, содержащихся в термах вида 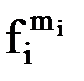( 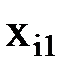, , 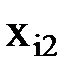…, ), (i=1, 2, …, n)) – множество k-местных операций на U.

Алфавитязыка чистогоисчисления предикатов первого порядка не содержит функциональных символов; термом в этом языке является только отдельно стоящая индивидная константа или переменная; поэтому интерпретационнаяфункция для чистого исчисления предикатов сопоставляет каждому константному терму (индивидной константе) определенный объектиз области интерпретации.

Каждой замкнутойбескванторной формуле A языка логики предикатов первого прядка (т.е. формуле, не содержащей свободныхвхождений индивидных переменных и в общем случае не содержащей функциональных и предикатных переменных) интерпретационная функция J сопоставляет, в конечном счете, один из двух абстрактных предметов: истину или ложь. Какой абстрактный предмет будет сопоставлен замкнутой формуле A интерпретационной функцией J, определяется однозначно строением формулы A и тем, какие предикаты приписываются предикатным константам, какие операции приписываются функциональным константам и какие предметы из Uприписываются индивидным константам.

Кванторным формулам интерпретационная функцияJ приписываетзначение истина (и) или ложь (л)в соответствии с семантическими правилами ПС.3.4."и ПС.3.5.$.

Каждой формуле языка чистого исчисления предикатовпервого порядка, не содержащей предикатных переменных и содержащей свободные вхождения nиндивидных переменных A(x₁,, x₂,, …, x_n),интерпретационная функция ставит в соответствие n-местный предикат, т.е. в стандартной теоретико-множественнойинтерпретации – множество упорядоченных n-ок предметов из U.

Вторым важным семантическим понятием является «последовательность j приписывания значений переменным»; это функция, которая сопоставляет:

(1) пропозициональным переменным – один из двух абстрактных предметов и,л;

(2) индивидным переменным–предметы из области U;

(3) n-местным функциональным переменным – n-местные операции на U;

(4) n-местным предикатным переменным – n-местные предикаты на U(т.е. множестваупорядоченных n-ок предметов из U).

Таким образом, последовательность j приписывания значений переменным сопоставляет значения переменным символамязыка логики предикатов первого порядка, т.е. это понятие служит для уточнения таких выражений логическойсемантики, как «набор значений переменных» и т.д. Выражения типа «индивидная переменная пробегает по области U», «n-местная предикатная переменная принимает значения в области множеств n-ок предметов из U» и т.д. записываются в семантическом метаязыке логики предикатов первого порядка с помощью предикатов, содержащих индивидные метапеременные j, y, j₁, …, пробегающие по последовательностям приписывания значений переменным языка-объекта.

В стандартных теоретико-множественных семантических теориях используются два наиболее общих способа определения функции j – последовательности приписывания значений переменным.

I способ: в качестве области определения функции j рассматривается подсписок алфавита ЯЛП, содержащий все переменные символы; их, как правило, счетно-бесконечное множество, или бесконечная последовательность; поэтому область определения функции j здесь отождествляется с бесконечной последовательностью, i-тый член которой является i-той переменной в списке переменных ЯЛП.

Последовательность всех переменных символов ЯЛП можно построить следующим образом:

(а) берем пересчеты пропозициональных и индивидных переменных:

p, q, r, p₁ , q₁ , r₁ , p₂ , q₂ , r₂ , …

x, y, z, x₁ , y₁ , z₁ , x₂ , y₂ , z₂ , …

(b) на основе бесконечной матрицы функциональных символов:

f ¹, g¹, h¹, , , , , , , , , , …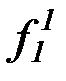

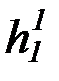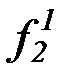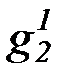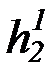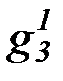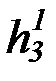f ², g², h², , , , , , , , , ,…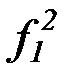

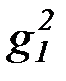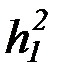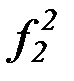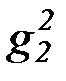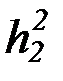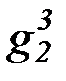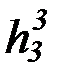f ³, g³, h³, , , _, , , , , , ,…

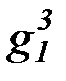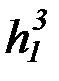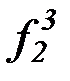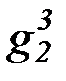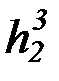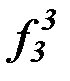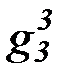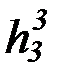f ⁴, g⁴, h⁴, , , , , , , , , , …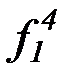

… … … … … … … … … … … .

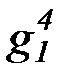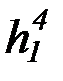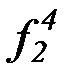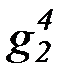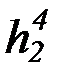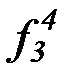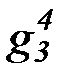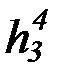строим пересчет (по принципу плоского порядка) функциональных символов:

f¹,g¹,h¹, 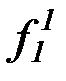, , 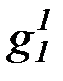, 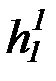f²,g²,h², 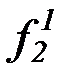, , 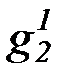, , 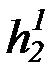, , 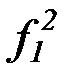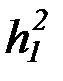f ³, g³, h³, …

(с) аналогично (b) строим пересчет предикатных символов:

P¹,Q¹,R¹, 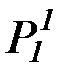, , 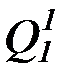,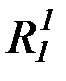P²,Q²,R², 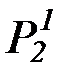, , 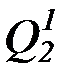, , 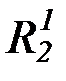, ,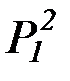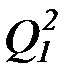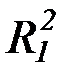P³, Q³, R³, …

(d) сводим пересчеты (a), (b) и (c) в матрицу:

p, q, r, p₁ , q₁ , r₁ , p₂ , q₂ , r₂ , p₃ , q₃ , r₃ , p₄ , q₄ , r₄ , …

x, y, z, x₁ , y₁ , z₁ , x₂ , y₂ , z₂ , x₃ , y₃ , z₃ , x₄ , y₄ , z₄ …

f ¹, g¹, h¹, 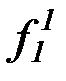, g¹₁ , 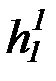, f ², g², h², , , , , , …

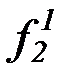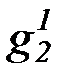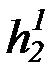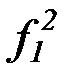P¹, Q¹, R¹, 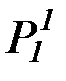, , 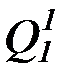, 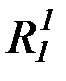P², Q², R², , , , , …

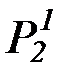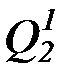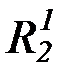и строим пересчет всех переменных символов ЯЛП

p, q, r, x, y, z, f ¹, g¹, h¹, P¹, Q¹, R¹, , p₁ , q₁ , r₁ , x₁ , y₁ , z₁ , 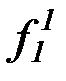, , 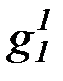, , 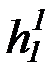, , 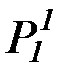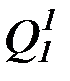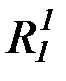p₂ , …

II способ: в качестве области определения функции j рассматривается список переменных ЯЛП, входящих свободно в ППФ A(в ЯЛП первого порядка все пропозициональные, функциональные и предикатные переменные являются свободными); пусть этот список обозначается [A]; тогда набор значений, сопоставляемый функцией j переменным, входящим в ППФ A, обозначим |[A]|.

Говорят, что j₁есть расширениеj₂(аj₂–сужениеj₁), если j₂ определена на [A], а j₁ на [B], [A] есть подсписок [B] (т.е. каждый элемент списка [A] входит в [B]), и j₁ приписываеткаждому элементу из [A] тот же объект, что и j₂.

На основе введенных выше семантических понятий можно определить семантический предикат«… есть значение терма t в полумодели áU,Jñ при последовательности j приписывания значений переменным» индукцией по определению терма. Напомним, что термом tявляется:

(1) отдельно стоящая предметная константа a ;

(2) отдельно стоящая предметная переменная x;

(3) выражение вида, Фⁿ(t₁, t₂, …, t_n), где Фⁿ – функциональная n-местная константа; t₁, t₂, …, t_n – термы;

(4) выражение вида f ⁿ(t₁, t₂, …, t_n), где f ⁿ – функциональная n-местная переменная; t₁, t₂…, t_n – термы.

Будем использовать выражение½t½ как сокращение выражения «значение t в полумодели áU,Jñ при последовательности j приписывания значений переменным».

Значением терма t в полумодели áU,Jñ при последовательности j приписывания значений переменнымявляется:

(Т1)если терм t есть предметная константа а, – тот индивид из области интерпретации U, который интерпретационная функция Jсопоставляет предметной константе а: ½а½= J(а) ;

(Т2) если терм tесть предметная переменная x, – тот индивид, который функция j сопоставляет индивидной переменной x, то есть:½х½= j(х);

(Т3) если терм tесть выражение вида Фⁿ(t₁, t₂, …, t_n,), где Фⁿ – функциональная n-местная константа; t₁, t₂, …, t_n – термы, то:

½Фⁿ(t₁, t₂, …, t_n,) ½= [J(Фⁿ)](½t₁½, ½t₂½, …, ½t_n½),

где: [J(Фⁿ)] – обозначение той n-местной операции на U, которую функция J сопоставляет функциональной константе Фⁿ;

½t_i½– значение терма t_i в полумодели áU,Jñ при последовательности jприписывания значений переменным (i = 1, …, n);

(T4) если терм tесть выражение вида f ⁿ(t₁, t₂, …, t_n), где f ⁿ – функциональная n-местная переменная; t₁, t₂…, t_n – термы, то:

½f ⁿ(t₁, t₂, …, t_n,)½=[j(f ⁿ)](½t₁½, ½t₂½, …, ½t_n½),

где: [j(f ⁿ)] – обозначение той n-местной операции на U, которую последовательность j приписывания значений переменным сопоставляет функциональной переменной f ⁿ;

½t_i½ – значение терма t_i в полумодели áU,Jñ при последовательности приписывания j значений переменным (i = 1, …, n).

Следующий важный семантический предикат «… (есть) значение правильно построенной формулы А в полумодели áU,Jñ при последовательности j приписывания значений переменным» определяется индуктивно по строению ППФ ЯЛП1⁼. Напомним, что ППФ ЯЛП1⁼ является:

(1) отдельно стоящая пропозициональная константа;

(2) отдельно стоящая пропозициональная переменная;

(3) выражение вида Aⁿ(t₁, t₂, …, t_n,),

где: Aⁿ – n-местная предикатная константа; t₁, t₂, …, t_n – термы;

(4) выражение вида Pⁿ(t₁, t₂, …, t_n,),

где: Pⁿ – n-местная предикатная переменная; t₁, t₂, …, t_n - термы;

(5) выражение вида "_xA,

где: " – знак квантора общности (употребляется автонимно); x– индивидная переменная;

(6) выражение вида $ _xA,

где: $ – знак квантора существования (употребляется автонимно); x–индивидная переменная;

(7) выражения вида ØA, (AÙB), (AÚB), (A®B), (A«B),

где: A, B – ППФ ЯЛП; Ø, Ù, Ú, ®, « – знаки коннекторов (употреблены автонимно); скобки употреблены автонимно;

(8) выражение вида (t₁= t₂), где t₁, t₂ – термы, = – знак равен ства (используется автонимно).

ППФ, указанные в (3) и (4), называются элементарными формуламиЯЛП1⁼.

Обозначая сокращенно выражение «… есть значение правильно построенной формулы A в полумодели áU,Jñ при последовательности j приписывания значений переменным»посредством «½А½= … при j», определяем по пунктам фундаментального индуктивного определения ППФ:

(1) если А есть отдельно стоящая пропозициональная константа, то ½А½=J(A) при j, то есть значение ППФ в полумодели áU,Jñ при последовательности j приписывания значений переменным совпадает в этом случае с тем значением (иили л), которое приписывает этой пропозициональной константе интерпретационная функция J в данной полумодели áU,Jñ;

(2) если А есть отдельно стоящая пропозициональная переменная p , то½А½=j(p) при j; то есть значение ППФ в полумодели áU,Jñ при последовательности jприписывания значений переменным совпадает в этом случае с тем значением (иили л), которое приписывает этой пропозициональной переменной функция j;

(3) ½Аⁿ(t₁, t₂, …, t_n,)½=ипри j, если и только если предикат J(Aⁿ) ставит в соответствие упорядоченной n-кe á½t₁½, ½t₂½, …, ½t_n½ñ значение и, или, другими словами, если и только если á½t₁½, ½t₂½, …, ½t_n½ñÎ J(Aⁿ) (здесь предикат отождествляется с множеством упорядоченных n-ok);

(4) ½Pⁿ(t₁, t₂, …, t_n,)½= ипри j, если и только если предикат j(Рⁿ) ставит в соответствие упорядоченной n-кe á½t₁½, ½t₂½, …, ½t_n½ñ значение и(т.е. á½t₁½, ½t₂½, …, ½t_n½ñ Îj(Рⁿ)).

Введем обозначения:

пусть х, х₁, х₂, …, х_n – список всех предметных переменных, содержащихся в формуле "_xA (или $ _xA ) и пусть j(x)=a, j(x_i)=a_i (i=1, …, n); тогда:

(5) ½"_xA½=ипри j, если и только если для любого bÎUверно, что ½A½=ипри приписывании переменной x значения b, а переменным x_i значений а_i (i=1, …, n), то есть если и только если ½A½= и при любом приписывании j₁, отличном от приписывания j возможно только значением j₁(х);

½"_xA½=л при j, если и только если существует bÎU такой, что ½A½=л при приписывании x значения b, а x_i значений а_i (i=1, …, n); т.е. если и только если существует такое приписывание j₁, отличное от приписывания j возможно только значением j₁(х), что ½A½=л при приписывании j₁;

(6) ½$_xA½=и при j, если и только если существует bÎU,такой, что ½A½=и при приписывании x значения b, а x_i значений а_i (i=1, …, n); т.е. если и только если найдется такое приписывание j₁, отличное от j возможно лишь значением для переменной x, что½A½=ипри j₁;

½$_xA½=лпри j, если и только если для любого bÎUверно, что ½A½=и при приписывании x значения b, а всем x_i – значений а_i= j₁(х_i) (i=1, …, n) ; т.е. если и только если ½A½=лпри любом приписывании j₁, отличном от j не более чем значением для переменной x;

(7) (7.1) ½ØA½=и при j , если и только если ½A½=лпри j; ½ØA½=л при j , если и только если½A½= и при j;

(7.2) ½(AÙB)½=и при j, если и только если ½A½=и при j и ½В½=и при j ;

½(AÙB)½=л при j, если и только если ½A½=л при j или ½В½=л при j;

(7.3) ½(AÚB)½=и при j, если и только если ½A½=и при j или ½В½=и при j;

½(AÚB)½=л при j, если и только если ½A½=л при j и ½В½=л при j;

(7.4) ½(A®B)½=и при j, если и только если ½A½=л при j или ½В½=и при j;

½(A®B)½=л при j, если и только если ½A½=и при j и ½В½=л при j;

(7.5) ½A«B½=и при j, если и только если ½A®B½=и при j и ½В®А½=и при j;

½A«B½=л при j, если и только если ½A®B½=л при j или ½В®А½=л при j;

(8)½ t₁= t₂½=и при j, если и только если½t₁½= ½t₂½;

½t₁= t₂½=л при j, если и только если неверно,что½t₁½= ½t₂½(½t₁½¹ ½t₂½).

Основной семантический предикат«последовательность j выполняет ППФ A в полумодели áU,Jñ», сокращенно Вып(j, A, áU,Jñ),теперь вводится следующим определением:

Вып(j, A, áU,Jñ), если и только если½A½= и при j.

На основе определения предиката Вып(j, A, áU,Jñ) вводятся семантические предикаты, представляющие в ЯЛФРТ важнейшие свойства суждений и отношения между ними. Кванторы в нижеследующих выражениях – знаки метаязыка; знак =* – «графически равно».

Формула А общезначима (истинна) в полумодели áU,Jñ,сокращенноОбщ(А, áU,Jñ), если и только если всякий набор значений свободных переменных формулы А (т.е. всякая последовательность jприписывания значений переменным из списка [A]) выполняет формулу А в полумодели áU,Jñ; символически:

Общ(А, áU,Jñ)=_Df "j Вып(j, A, áU,Jñ)

(=_Dfозначает «равно по определению»).

Формула А выполнима в полумоделиáU,Jñ,если и только если существует набор значений свободных переменных формулы А (т.е. последовательность приписывания j значений свободным переменным из списка [A]) такой (-ая), что этот набор (эта последовательность) выполняет формулу А в полумодели áU,Jñ:

Вып(А, áU,Jñ)=_Df $j Вып(j, A, áU,Jñ).

Если ППФ А выполнимав полумодели М=*áU,Jñ, то Мназывается модельюдля формулы А.

Формула А выполнима на универсуме U,если и только если существует интерпретация J такая, что А выполнима в полумодели áU,Jñ; символически:

Вып(А,U) =_Df $_J Вып(A, áU,Jñ)=*$ _J $j Вып(j, A, áU,Jñ).

Формула А выполнима,если и только если существует такой универсум U, что А выполнима на универсуме U:

Вып(А) =_Df $_U Вып(A, U)=* $_U $ _J $j Вып(j, A, áU,Jñ).

Формула А общезначима (истинна) на универсуме U:

Общ(А,U)=_Df "_J Общ (A, áU,Jñ)=*" _J "j Вып(j, A, áU,Jñ).

Формула А общезначима (логически истинна):

Логической формой некоторого выражения естественного языка называется перевод этого выражения на ЯЛФРТ, в котором всенелогические константы заменены переменными соответствующих категорий таким образом, что ни одна индивидная переменная не оказывается в области действия квантора, связывающего эту переменную.