Алфавит языка и его синтаксис

Определение языка можно разбить на 4 части: символы (characters), высказывания (tokens), синтаксис (syntax) и семантика (semantics) – толкование.

Алфавит языка содержит 26 прописных и строчных латинских букв (от a до z) (прописные и строчные буквы различаются) 10 арабских цифр (от 0 до 9) и 32 специальных символа:

· арифметические операторы +, –, *, /;

· знак возведения в степень ^;

· 5 пар альтернативных символов: ^ – **, [ – (|, ] – |), { – (*, } – *);

· : – фиксатор выражения, предотвращающий вывод результата вычисления в ячейку вывода;

· ; – фиксатор выражения, дающий вывод результата вычисления в ячейку вывода;

· # – указатель программного комментария;

· ‘ – ограничитель строки;

· := – оператор присваивания;

· ;; – пустой оператор;

· :: – указатель типа переменной (n::integer или z::complex).

Высказываниями (лексемами) являются ключевые слова, операторы программирования, строки, натуральные числа и знаки препинания.

Зарезервированные слова – имеют специальное значение и их нельзя применять в качестве идентификаторов.

Операторы программного языка. Имеются 3 типа операторов (binary, unary, nullary): двуместные (бинарные), одноместные (унарные), и нульарные – не имеющие операндов. Последних всего 3 (ditto–операторы) обращения к предыдущему вычислению (%,%%,%%%)

Высказывания можно разделять пустыми операторами или знаками препинания.

Пустые разделители – это пробелы, знаки табуляции и возврат каретки. Пробелы нельзя использовать внутри высказываний (лексем), но можно между лексемами. В строках, заключенных в обратные кавычки, они становятся частью высказывания.

>a*x+x*y; # комментарий

ax+xy

Перейти на новую строку с продолжением записи команды можно, нажав клавиши Shift–Enter.

Выражения

Выражение может содержать операторы, операнды и функции с параметрами. Строка ввода математических выражений имеет отличительный символ >, а строка ввода текстов никаких признаков не имеет. Встречая выражение, Maple оценивает его, т.е. если выражение – скалярная переменная, то её значение будет выведено в ячейке вывода. Для переменных более сложных типов выводится не их значение, а просто повторяется имя переменной. Просто повторяются также имена неопределенных переменных.

Важным понятием системы Maple (да и математики вообще) является понятие функции. Функция возвращает результат некоторого преобразования исходных данных – параметров функции по определенному правилу, обычно представленному в виде формулы или программного модуля. Maple имеет множество встроенных функций, включенных в его ядро и в пакеты.

Функция в выражениях задается вводом ее имени и списка параметров функции (одного или нескольких), заключенного в круглые скобки: например, sqrt(2) задает функцию вычисления квадратного корня с параметром 2 (численной константой). Основным признаком функции является возврат значения в ответ на обращение к ней по имени (идентификатору) с указанием списка параметров функции. Например:

> 2*sin(1.);

1.682941970

> 2*sin(1);

2 sin(1)

Обратите внимание на особую роль десятичной точки – здесь она служит указанием к выполнению вычисления значения sin(1.0) (или, что то же самое, sin(1.)). А вот синус целочисленного аргумента 1 не вычисляется – считается.

Помимо функций, для записи математических выражений используется специальные знаки – операторы. К примеру, вычисление квадратного корня часто записывается с помощью его специального знака — √. Достаточно хорошо известны операторы сложения +, вычитания -, умножения деления / и некоторые другие. Операторы обычно используются с операндами в виде констант или переменных, например в записи 2*(3+4) числа 2, 3 и 4 — это операнды, а знаки * и + — операторы. Скобки используются для изменения порядка выполнения операций. Так, без них 2*3+4=10, тогда как 2*(3+4)=14, поскольку вначале вычисляется выражение в скобках.

Пожалуй, самым распространенным оператором является оператор присваивания :=. Он используется для задания переменным конкретных значений, например:

> х:=у;

х := у

> у:=z;

y := z

> z:=2;

z := 2

> х;

> у;

В этом примере переменные х, у и z взаимосвязаны с помощью операций присваивания. Поэтому задание значения 2 переменной z приводит к тому, что и переменные у и х принимают то же значение.

Другой распространенный оператор – оператор равенства = используется для задания равенств и логических условий (например, а=b), указания областей изменения переменных (например, i=1..5 означает формирование диапазона изменения i от 1 до 5) и определения значений параметров в функциях и командах (например, color=black для задания черного цвета у линий графиков).

Операторы сами по себе результат не возвращают. Но они, наряду с функциями и своими параметрами (операндами), позволяют конструировать математические выражения, которые при их вычислении также возвращают результат.

Для оценивания выражений применяются следующие функции:

· eval(array) – возвращает содержимое массива array;

· evalf(выражение, n) – вычисляет выражение и возвращает вычисленное значение в форме числа с плавающей точкой, имеющего n цифр после десятичной точки;

· evalhf(выражение) – вычисляет выражение и возвращает вычисленное значение с точностью, присущей данной компьютерной системе;

· evalm(матричное выражение) – вычисляет значение матричного выражения и возвращает его;

· evalb(логическое условие) – вычисляет значение логических условий;

· evalc(комплексное выражение) – вычисляет значение комплексного выражения;

· shake(выражение, амплитуда) – вычисляет интервальное выражение.

Примеры:

> evalf(sin(1));

0.8414709848

> evalb(1<3);

true

Последовательность выражений – это ряд выражений, разделенных запятыми и завершенных фиксатором:

>1,2+3,a-b,sin(1.0);

1, 5, a–b, 0.8414709848

Для автоматического формирования последовательности выражений применим специальный оператор $, после которого можно указывать число выражений или задавать диапазон формирования выражений:

>f$5;

f, f, f, f, f

>$1..6;

1, 2, 3, 4, 5, 6

>(i^2+1)$i=1..5;

2, 5, 10, 17, 26

>V[i]$i=1..5;

V[1], V[2], V[3], V[4], V[5]

Для создания последовательности выражений можно использовать функцию seq:

>seq(2*sin(x/10.0),x=0..5);

0, 0.1997, 0.3973, 0.5910, 0.7788, 0.9589

>seq(f(1),f=[sin,cos,tan]);

sin(1), cos(1), tan(1)

>seq(f(1.0),f=[sin,cos,tan]);

0.8415, 0.5403, 1.5574

Типы данных

Числа и числовые константы. Maple работает с числами следующего типа:

· целыми десятичными (0, 1, –123);

· рациональными в виде отношений целых чисел (7/9, –123/27);

· вещественными с мантиссой и порядком (1.23E5);

· комплексными (2+3I). Мнимая единица обозначается I.

Функции Re(x) и Im(x) возвращают действительную и мнимую часть комплексных чисел.

Десятичная точка в числах имеет особый статус: указание её в любом месте числа, а также в конце, делает число вещественным и ведет к переводу вычислений в режим вычислений с вещественными числами. При этом количеством выводимых после десятичной точки цифр можно управлять с помощью значения системной переменной Digits:

>restart;

>2+3/4;

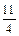
>2+3*4;

>1.0/3;

.3333333;

>Digits:=3;

>1.0/3;

.333;

>x:=2+7*I;

x:=2+7I;

>Re(x);

>Im(x);

Встроенные константы:

· false, true – ложно, истинно;

· gamma – константа Эйлера, равная 0.5772156649…;

· infinity – положительная бесконечность (отрицательная задается как –infinity);

· Catalan – константа Каталана, равная 0.915965594…;

· I – мнимая единица;

· Pi – 3.141….

В список не входит основание натурального логарифма – число e. В качестве этой константы можно использовать exp(1). Оно отображается как жирная прямая буква e. А exp(1.0) выводит 2.71828….

Контроль за числами и константами. Числа могут служить объектами ввода, вывода и константами, входящими в математические выражения. Функция

type(x,numeric)

позволяет выяснить, является ли x числовой константой. Если да, то функция возвращает логическое значение true, если нет – false.

>type(10,numeric);

true

>type(Pi,numeric);

true

>type(x^3,numeric);

false

Функции

type(x,integer)

type(x,racional)

type(x,fraction)

можно использовать для оценки того, имеет ли x значение целого, рационального числа или простой дроби.

Функции

type(x,constant)

type(x,realcons)

возвращают значение true, если x представляет целочисленную или вещественную константу, и false в противном случае.

Преобразование чисел с разными основаниями. Возможна работы с числами, имеющими различное основание (base), бинарными числами (основание 2 – binary), восьмеричными (основание 8 – octal), шестнадцатеричными (основание 16 – hex). Функция convert позволяет преобразовывать форматы чисел:

>x:=12345;

x:=12345

>b:=convert(x,binary);

b:=11000000111001

>o:=convert(x,octal);

o:=30071

>h:=convert(x,hex);

h:=3039

Строковые данные – это последовательности символов, заключенные в обратные апострофы. Два апострофа подряд формируют апостроф как знак символьной строки.

>`2+2 не всегда ``четыре```;

2+2 не всегда ‘четыре’

Вектора и матрицы. Для создания векторов и матрицы служит функция array:

· array[i1..i2,s1] – возвращает вектор с индексами от i1 до i2 и значениями в одномерном списке s1;

· array[i1..i2,j1..j2,s2] – возвращает матрицу с номерами строк от i1 до i2, столбцов от j1 до j2 и значениями в двумерном списке s2.

Следует отличать списки от массивов! Массивы создаются с помощью функции array и являются отдельным типом данных.

>array(1..3,[x,y,x+y]);

[x, y, x+y]

>array(1..2,1..2,[[a,b],[c,d]]);

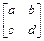
Таблицы задают множественные данные с произвольной индексацией. Для создания таблиц служит функция table, которая в простейшем виде table() создает шаблон пустой таблицы:

>table();

table([]);

Переменные. Переменные – это объекты, значения которых могут изменяться по ходу выполнения документа. Тип переменных определяется присвоенным им значением. Для явного указания типа переменных используется конструкция:

имя_переменной::тип

Типы переменных:

· integer – целочисленные;

· racional – рациональные;

· real – вещественные;

· complex – комплексные;

· float – вещественные с плавающей точкой;

· string – строчные;

· nonneg – значение >=0.

Имена переменных должны начинаться с буквы. Строчные и прописные буквы различаются между собой.

По умолчанию любые переменные рассматриваются как объекты символьного типа. Не требуется предварительное описание переменных. Для присваивания переменным конкретных значений используется оператор присваивания (:=).

Для отмены присваивания значений всем переменным используется команда restart;

>x:=10;

x:=10

>2*x^2;

>restart;

>x;

x

>2*x^2;

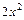
Переменные могут иметь определенные признаки, например принимать только положительные значения и т.д. Для придания переменным статуса предполагаемых используется оператор assume:

assume(переменная или выражение, свойство)

>assume(x,positive);

>x;

x~

Переменная помечена как положительная и при выводе сопровождается знаком тильды. Для того, чтобы к имеющимся признакам добавить новые, используется функция additionally:

>additionally(a<=0);

Для получения информации о статусе переменной используется функция about:

about(переменная)