Cхема 2.3. Семантика предложения ЯЛФРТ
Пример 2.2.Предложения «Сократ – человек», «Земля – планета», «2×2=4» являются именами абстрактного предмета истина, а предложения «Сократ – бог», «Земля – звезда», «2×2=5» обозначают абстрактный предмет ложь.
Функторы – это неполные выражения ЯЛФРТ, то есть выражения с пустыми местами. Каждый функтор ЯЛФРТ содержит одно или несколько пустых мест, замещаемых выражениями ЯЛФРТ, которые называются аргументами функтора; в зависимости от количества пустых мест функторы бывают одноместными или многоместными (двухместными, трехместными и т.д.). Каждое пустое место имеет одно или несколько вхождений в функтор; если имеется несколько вхождений пустого места в функтор, то они могут быть упорядочены естественным образом («первое вхождение пустого места в функтор», «второе вхождение» и т.д.). Как правило, предполагается, что функторы ЯЛФРТ имеют конечное (хотя и неограниченное) число мест и конечное число вхождений пустых мест. Замещение пустых мест выражениями ЯЛФРТ может быть двух видов: (1)подстановкаязыкового выражения на пустое место в функтор; при подстановке все вхождения некоторого пустого места в функтор замещаются подставляемым выражением; (2) замена пустого места; при замене происходит замещение только некоторых вхождений пустого места в функтор выражением ЯЛФРТ.
Результат замещения всех вхождений пустых мест в функтор выражениями ЯЛФРТ называется замыканием функтора. Говорят, что функтор действует на аргументы: переводит аргументы в замыкание.
В качестве аргументов и замыканий функторов могут использоваться как полные выражения ЯЛФРТ (имена и предложения), так и функторы. Простые функторы ЯЛФРТ переводят полные выражения в полные. Среди аргументов и/или замыканий сложных функторов ЯЛФРТ обязательно встречаются функторы, то есть неполные выражения.
Аналогов функторов в естественном языке нет. Это обусловлено принципиальным отличием структуры сложных выражений естественного языка и ЯЛФРТ. Сложное выражение естественного языка «порождается» в некотором процессе, протекающем во времени; структура этого процесса фиксируется строением сложного выражения. Например, строение предложения «Книга лежит на столе» в естественном языке передается конструкцией (1): «(Кто? Что?) Книга (Что делает? В каком состоянии находится?) лежит (Где?) на столе» или конструкцией (2): «Кто? Что?) Книга (Что делает? В каком состоянии находится?) лежит (На чем?) на столе». Эти две конструкции фиксируют два разных процесса диалогического характера (два языковых диалога, две языковые игры), в каждом из которых предполагается вопрос и ответ на этот вопрос. Поскольку вопросы в этих диалогах разные, мы имеем дело с двумя предложениями естественного языка; в первом из них имеется обстоятельство места «(Где?) на столе», а во втором – дополнение «(На чем?) на столе». В ЯЛФРТ сложное выражение получается путем замещения пустых мест в функторе; так, предложение «Книга лежит на столе» в ЯЛФРТ есть результат подстановки двух имен: «книга» и «стол» соответственно на первое и второе пустые места в функторе « . . . лежит на * * * » (пустые места обозначены «. . .» и «* * *»). В контексте данного предложения слова естественного языка «книга» и «стол» являются именами ЯЛФРТ, так как каждое из них называет один единственный предмет из универсума рассуждения.
Таблица 2.1. Простые функторы ЯЛФРТ
| название функтора | аргументы | замыкание | примеры |
| оператор | имена | имя | «отец ...», «... + 1», «(. . . + * * *) : ...» |
| предикатор | имена | предложение | «. . . (есть) отец», «... – отец * * *», «. . . < 5», «. . . + * * * = 101» |
| коннектор | предложения | предложение | «неверно, что ...» –отрицание; «... и * * *» –конъюнкция; «... или * * *» –дизъюнкция (альтернатива); «если ..., то * * *» –импликация; «...если и только если * * *» – эквиваленция. |
| субнектор* | предло-жения | имя | «тот самый, который . . .» |
* Вообще говоря, субнектор не является простым функтором ЯЛФРТ; поскольку в ЯЛФРТ принимается основная идеализация, здесь в принципе невозможны простые функторы, переводящие предложения в имена. Функтор определенной дескрипции, введенный Б. Расселом, на самом деле переводит в имя некоторый предикатор (неполное предложение) при условии доказательства существования и единственности предмета, имя которого при подстановки в предикатор превращает его в истинное предложение.
Сложные функторы ЯЛФРТимеют в качестве аргументов функторы. Наиболее употребительными сложными функторами являются кванторы, абстрактор и классообразователь (функтор множества).
Квантор – это сложный функтор ЯЛФРТ, переводящий одноместный предикатор в предложение путем связывания пустого места в предикаторе.
До сих пор мы имели дело с одним способом образования простых предложений в ЯЛФРТ: подстановкой имен в предикатор. Кванторы дают возможность образовать из одноместного предикатора предложение без подстановки – путем связывания пустого места. В ЯЛФРТ используются два вида кванторов: квантор существованияи квантор общности.
Рассмотрим предложение естественного языка:
(1) «Некто есть отец Лжедмитрия I».
Грамматическая структура этого предложения совпадает с грамматической структурой предложения естественного языка
(2) «Иван Грозный есть отец Лжедмитрия I»
и выражается диалогической конструкцией:
«(Кто? Что?) Некто (Что делает? В каком состоянии
находится?) есть отец (Кого? Чего?) Лжедмитрия I».
В ЯЛФРТ предложения (1) и (2) должны быть получены путем устранения(элиминирования) пустых мест в предикаторе «…есть отец ***». Второе пустое место (***) устраняется (элиминируется) в обоих случаях подстановкой имени «Лжедмитрий I». Первое пустое место (…) при образовании предложения (2)устраняется подстановкой имени «Иван Грозный». Как устраняется первое пустое место в предикаторе «…есть отец ***» при образовании предложения (1)? Грамматика естественного языка «подсказывает» подстановку вместо пустого места имени «некто»; однако местоимение «некто» не является именем в ЯЛФРТ, поэтому этот способ элиминирования пустого местане годится в данном случае. Вместе с тем, предложение (1) является осмысленным и даже истинным; поэтому оно должно быть представлено в ЯЛФРТ и обозначать абстрактный предмет и. Для нахождения способа представления предложения (1)в ЯЛФРТ заметим, что в этом предложении не называется имени отца Лжедмитрия I, а лишь констатируется его существование; то есть смысл предложения (1) может быть более точно выражен предложением:
(1') «Существует человек, который есть отец Лжедмитрия I».
Для трансформации этого предложения в предложение ЯЛФРТ достаточно ввести пустые места:
(1'') «Существует … (есть) человек, такой что [… (есть) отец Лжедмитрия I]».
Выражение «Существует … (есть) человек, такой что [+++]» рассматривается в ЯЛФРТ как сложный функтор, содержащий в своем составе одно пустое место «+++», замещаемое предикатором «…есть отец Лжедмитрия I», в составе которого имеется пустое место «…», входящее в выражение сложного функтора. Этот сложный функтор называется квантор существования. Пустое место «+++» называют областью действия квантора существования (обозначена квадратными скобками). Предложение (1'') получено в результате действия квантора существования на одноместный предикатор «…есть отец Лжедмитрия I». Поскольку выражение (1'') является предложением, оно не может содержать пустых мест; следовательно, действие квантора существования на предикатор заключается в том, что пустое место, входящее в состав предикатора, не может более замещаться именами, если предикатор находится в области действия квантора существования, содержащего данное пустое место. Говорят, что квантор связывает пустое место, входящее в его состав.
Квантор общности, как и квантор существования, вводится на основании анализа логической структуры предложений естественного языка. Как представить в ЯЛФРТ предложение естественного языка:
(3) «Лиса – хищное животное»?
Очевидно, в ЯЛФРТ нельзя получить данное предложение путем подстановки в предикатор «… – хищное животное» имени «лиса» вместо «…», так как выражение «лиса» не является именем в ЯЛФРТ, а является предикатором «…– лиса». Для представления в ЯЛФРТ заметим, что смысл предложения (3) в естественном языке более точно передается предложением:
(3') «Каждая лиса – хищное животное»,
что позволяет записать соответствующее выражение ЯЛФРТ путем введения пустых мест:
(3'') «Для каждой … – лиса, […– хищное животное]»,
и представить предложение (3'') как результат действия квантора общности «Для каждой …– лиса [+++]» на предикатор «…– хищное животное» (область действия квантора обозначена квадратными скобками).
Относительно выражений ЯЛФРТ с квантором общности справедливо все, что говорилось выше о выражениях ЯЛФРТ с квантором существования.
Таким образом, кванторные выражения ЯЛФРТ содержат в своем составе следующие компоненты.
(1) Выражения для кванторов, содержащие в своем составе пустые места, замещаемые индивидами, например: «Существует … (есть) человек, такой что [+++]», «Для каждой …– лиса [+++]».
(2) Выражения, находящиеся в области действия кванторов; в наших примерах: «…есть отец Лжедмитрия I», «…– хищное животное»; эти выражения часто называют подкванторные выражения.
(3) Пустые места, входящие в выражения для кванторов, называют квантифицируемыми; все вхождения этих пустых мест в выражения, находящиеся в области действия кванторов, называют связанными, или квантифицированными; связанные вхождения пустых мест не могут замещаться. Говорят, что квантор, содержащий данное пустое место, связывает все вхождения этого пустого места в области своего действия. Вхождения пустого места, находящиеся вне области действия квантора, содержащего в своем составе данное пустое место, называются свободными.
Пустое место может входить в квантор двумя способами: (1) в составе некоторого одноместного предикатора, как в рассмотренных выше случаях; (2) прямо, непосредственно: «Существует … такой, что [+++]», «Для каждого …[+++]». В первом случае кванторы называются ограниченными кванторами, а во втором – неограниченными.
Абстрактор и классообразователь будут рассмотрены ниже, после общих семантических правил ЯЛФРТ.
Выражения ЯЛФРТ представляют собой знаковые конструкции, составляемые из некоторых элементарныхстандартных знаков-символов(атомарных знаков, атомов). Все стандартные символы ЯЛФРТ разбиваются на две большие категории: постоянные символы (константы) и переменные символы (переменные). Постоянные символы – это стандартные обозначения для исходных выражений ЯЛФРТ различных семантических категорий; переменный символ – это пустое место с указанием семантической категории подставляемых на это пустое место выражений.
Таблица 2.2. Стандартные символы ЯЛФРТ
| семантическая категория | постоянные символы (константы) | переменные символы |
| имена | a, b, c, a1 , b1 , c1 ,a2 , ... именные, предметные, индивидные | x, y, z, x1 , y1 , z1 , x2 , y2 , ... именные, предметные, индивидные |
| предложения | A, B, C, 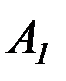 ,B1, ...,И,Л
пропозициональные ,B1, ...,И,Л
пропозициональные
| p, q, r, p1 ,q1 ,r1 , p2 , ... пропозициональные |
| операторы* | +2, -2, :2, sin1, lg1, ... операторные, функциональные | f 1,g1, h2, 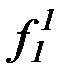 , , 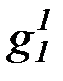 , , 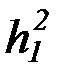 , ...
операторные, функциональные , ...
операторные, функциональные
|
| предикаторы* | A1, B1, C1, 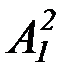 , , 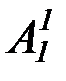 , ...
предикатные , ...
предикатные
| P1, Q1, R1, P2, 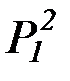 , , 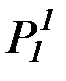 , ..., S1, M1, , ..., S1, M1, 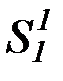 , , 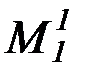 , …
предикатные , …
предикатные
|
| коннекторы (логические союзы, логические константы) | Ø, N – отрицание Ù, &,K – конъюнкция Ú, A – дизъюнкция Ú – исключающая дизъюнкция ®, É,С– импликация«, – эквиваленция | нет |
| кванторы | $ – квантор существования " – квантор общности | нет |
| абстрактор | l | нет |
| классообразователь (функтор множества) | { ½ } | нет |
* Верхний индекс константы указывает число мест соответствующего функтора; верхний индекс переменной указывает число мест подставляемого вместо этой переменной функтора.
В этой таблице отсутствуют символы для обозначения некоторых предикаторов и сложных функторов, играющих важную роль в логике; они будут вводиться в дальнейшем по мере необходимости.
Дата добавления: 2021-01-26; просмотров: 789;











