ПР№8. «Приближенное вычисление по формулам прямоугольников, трапеции, Симпсона»
ТЕМА 9
Задачи, приводящие к дифференциальным уравнениям. Задача Коши. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения. Однородные дифференциальные уравнения первого порядка. Линейные однородные уравнения второго порядка с постоянными коэффициентами
Обыкновенным дифференциальным уравнением 1 -го порядканазывается выражение вида 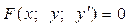 , т.е. уравнение, содержащее неизвестную, искомую функцию y=y(x) и ее производную.
, т.е. уравнение, содержащее неизвестную, искомую функцию y=y(x) и ее производную.
Решением дифференциального уравнения называется такая функция у=у(х), которая при подстановке ее в это уравнение обращает его в верное тождество.
Общим решением дифференциального уравнения 1-го порядка называется такое его решение 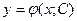 , которое является функцией переменной х и произвольной независимой постоянной С . (Независимость постоянных означает отсутствие каких-либо соотношений между ними).
, которое является функцией переменной х и произвольной независимой постоянной С . (Независимость постоянных означает отсутствие каких-либо соотношений между ними).
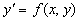 Определение:Задача нахождения решения уравнения , удовлетворяющего
Определение:Задача нахождения решения уравнения , удовлетворяющего
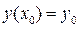 условию (4)
условию (4)
где числа 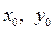 – заданные числа, называется задачей Коши. Условие (4) называется начальным условием.
– заданные числа, называется задачей Коши. Условие (4) называется начальным условием.
Решение уравнения , удовлетворяющее начальному
условию (4), называется решением задачи Кошии записывается в виде
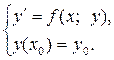 . (5)
. (5)
Решить задачу Коши (5) означает найти интегральную кривую дифференциального уравнения, которая проходит через заданную точку 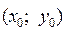 .
.
Примеры.
Пример№1: Решить дифференциальные уравнения:
а)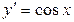 ; б)
; б) 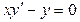 .
.
Решение:
а) Приведём уравнение к виду 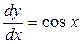 ;
; 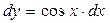 .
.
Интегрируем обе части уравнения: 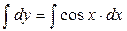 ;
; 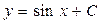 .
.
Ответ: 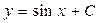 .
.
б) Приведём уравнение к виду : 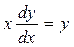 ;
; 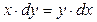 .
.
разделим обе части уравнения на 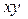 :
: 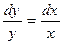 .
.
Переменные разделены. Интегрируем обе части уравнения:
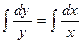 ;
; 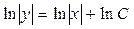 .
.
Применим основное логарифмическое тождество 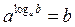 или
или 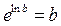 ,
,
получим
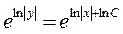 или
или 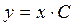 .
.
При делении на 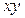 могли быть потеряны решения
могли быть потеряны решения 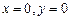 . Очевидно, что
. Очевидно, что 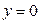 является решением данного уравнения при C=0, а
является решением данного уравнения при C=0, а 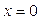 – нет. Таким образом, формула
– нет. Таким образом, формула 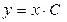 , где С – произвольная постоянная, задаёт все решения данного уравнения.
, где С – произвольная постоянная, задаёт все решения данного уравнения.
Ответ: 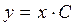 .
.
Пример №2: Найдите решения задачи Коши: а) 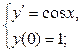 б)
б) 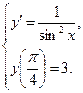
Решение:
а) 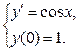 Найдём общее решение дифференциального уравнения.
Найдём общее решение дифференциального уравнения.
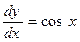 ;
; 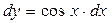 .
.
Интегрируем обе части уравнения: 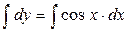 ;
; 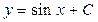 .
.
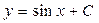 – общее решение дифференциального уравнения.
– общее решение дифференциального уравнения.
Подставим начальное условие в общее решение, получим
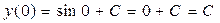 .
.
Так как по условию 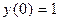 , то С=1. Тогда частное решение данного дифференциального уравнения имеет вид
, то С=1. Тогда частное решение данного дифференциального уравнения имеет вид 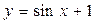 .
.
Ответ: 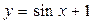 .
.
б) 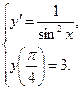 Найдём общее и частное решение дифференциального уравнения.
Найдём общее и частное решение дифференциального уравнения.
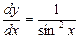 ;
; 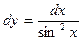 .
.
Интегрируем обе части уравнения: 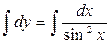 ;
; 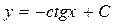 .
.
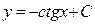 – общее решение дифференциального уравнения. Подставим начальное условие в общее решение, получим
– общее решение дифференциального уравнения. Подставим начальное условие в общее решение, получим 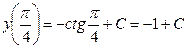 .
.
Так как по условию 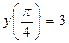 , то –1+С=3, С=4. Тогда частное решение данного дифференциального уравнения имеет вид
, то –1+С=3, С=4. Тогда частное решение данного дифференциального уравнения имеет вид 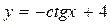 .
.
Ответ: 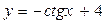 .
.
Дата добавления: 2021-01-26; просмотров: 542;











