Характеристическое уравнение имеет сопряженные комплексные корни
Если уравнение 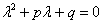 имеет сопряженные комплексные корни
имеет сопряженные комплексные корни 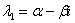 ,
, 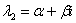 (дискриминант
(дискриминант 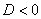 ), то общее решение однородного уравнения принимает вид:
), то общее решение однородного уравнения принимает вид: 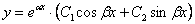 , где
, где 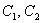 – константы.
– константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом: 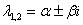
Пример.Решить однородное дифференциальное уравнение второго порядка
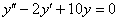
Решение: Составим и решим характеристическое уравнение:
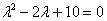
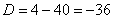
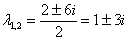 – получены сопряженные комплексные корни
– получены сопряженные комплексные корни
Ответ: общее решение: 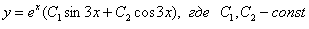
Пример.Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям 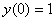 ,
, 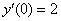
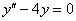
Решение: составим и решим характеристическое уравнение:
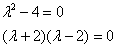
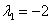 ,
, 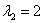
Получены два различных действительных корня, поэтому общее решение:
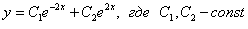
Алгоритм нахождения частного решения следующий:
Сначала используем начальное условие 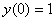 :
:
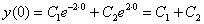
Согласно начальному условию, получаем первое уравнение: 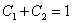
Далее берём наше общее решение 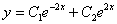 и находим производную:
и находим производную:
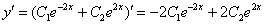
Используем второе начальное условие 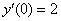 :
: 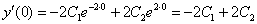
Согласно второму начальному условию, получаем второе уравнение: 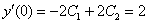 или просто
или просто 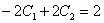
Составим и решим систему из двух найденных уравнений: 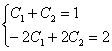
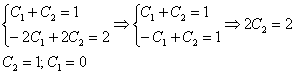
Подставим найденные значения констант 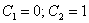 в общее решение
в общее решение 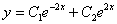 :
:
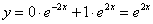
Ответ: частное решение: 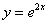
Примеры решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
Найти общие решения однородных дифференциальных уравнений второго порядка:
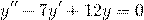
Составляем характеристическое уравнение: k²-7k+12=0. Его дискриминант D=b²-4ac=1>0, поэтому корни — различные действительные числа.
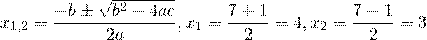
Отсюда, общее решение этого однородного ДУ 2-го порядка есть
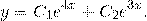
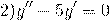
Составим и решим характеристическое уравнение: 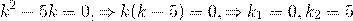 . Корни действительные и различные. Отсюда имеем общее решение данного однородного дифференциального уравнения:
. Корни действительные и различные. Отсюда имеем общее решение данного однородного дифференциального уравнения: 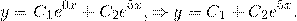
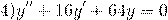
Характеристическое уравнение 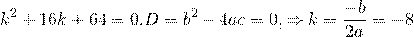
Поскольку корни действительны и равны, для этого дифференциального уравнения общее решение записываем как 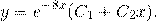
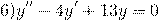
Характеристическое уравнение здесь 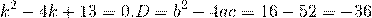
Так как дискриминант — отрицательное число, корни характеристического уравнения — комплексные числа.
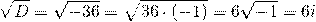
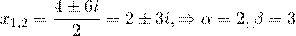
Общее решение этого однородного дифференциального уравнения второго порядка имеет вид 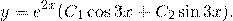
Примеры для самопроверки.
Найти общее решение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
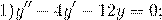
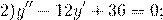
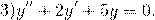
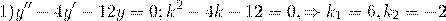 ;
; 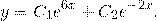
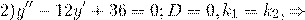
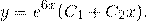
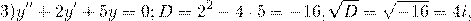
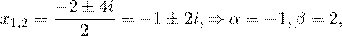
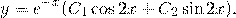
Дата добавления: 2021-01-26; просмотров: 1385;











