Решите следующие задачи.
1. Решите дифференциальные уравнения:
а) 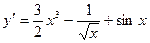 ; б)
; б) 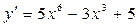 ; в)
; в) 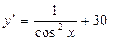 ;
;
г) 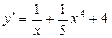 ; д)
; д) 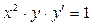 ; е)
; е) 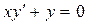 .
.
2. Найдите решения задачи Коши:
а) 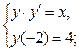 в)
в) 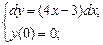 д)
д) 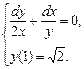
б) 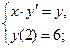 г)
г) 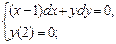
Дифференциальное уравнение второго порядка, содержит:
1) независимую переменную 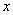 ;
;
2) зависимую переменную 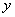 (функцию);
(функцию);
3) первую и вторую производную функции
Решить дифференциальное уравнение – это значит, найти множество функций 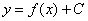 , которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.
, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.
2.Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:
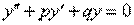 , где
, где 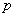 и
и 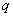 – константы (числа), а в правой части – строго ноль.
– константы (числа), а в правой части – строго ноль.
Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:
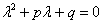
По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем 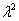 ;
;
вместо первой производной записываем просто «лямбду»;
вместо функции 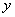 ничего не записываем.
ничего не записываем.
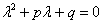 – это обычное квадратное уравнение, которое предстоит решить.
– это обычное квадратное уравнение, которое предстоит решить.
Существуют три варианта развития событий.
Характеристическое уравнение имеет два различных действительных корня
Если характеристическое уравнение 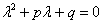 имеет два различных действительных корня
имеет два различных действительных корня 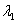 ,
, 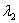 (т.е., если дискриминант
(т.е., если дискриминант 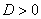 ), то общее решение однородного уравнения выглядит так:
), то общее решение однородного уравнения выглядит так:
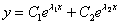 , где
, где 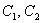 – константы.
– константы.
Пример.Решить дифференциальное уравнение 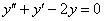
Решение: составим и решим характеристическое уравнение:
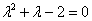
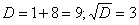
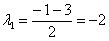 ,
, 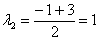
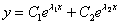
Ответ: общее решение: 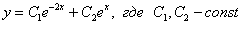
Дата добавления: 2021-01-26; просмотров: 513;











