Теорема о компенсации

Формулировка теоремы: любой пассивный элемент электрической схемы можно заменить а) идеальным источником напряжения с ЭДС, равной напряжению на этом элементе (E=U) и направленной навстречу току, б) иде­альным источником тока J, равным току в этом элементе (J=I) и направленным согласно току I.

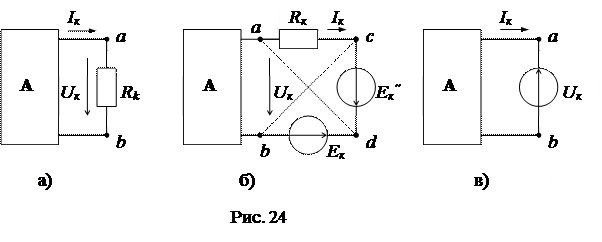Выделим пассивный элемент R_k с током I_k и напряжением U_k из схемы цепи (рис. 24а). Для доказательства п. а) теоремы включим последовательно с элементом R_k навстречу друг другу два идеальных источника ЭДС 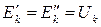(рис. 24б). Такое включение источников ЭДС не вызовет изменения режима сложной схемы, так как их действие взаимно компенсируется. Cоставим потен­циальное уравнение между точками “a” и “d” :

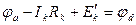, откуда следует 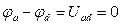, или .

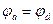
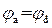Точки “a” и “d”, как точки равного потенциала, можно закоротить и за­короченный участок “a-d” из схемы удалить без нарушения ее режима. В ре­зультате удаления закороченного участка схема получает вид рис. 24в, в кото­рой пассивный элемент R_k заменен идеальным источником ЭДС .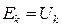

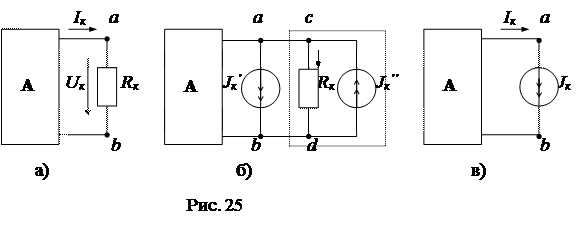Для доказательства п. б) теоремы включим параллельно с элементом R_k два идеальных источника тока 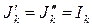, направленные навстречу друг другу (рис. 25б).

Такое включение источников тока 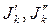не вызовет изменения режима сложной схемы, так как их действия взаимно компенсируются. С другой сто­роны ток в ветви “a-c” равен нулю ( 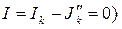, и эту ветвь можно отклю­чить без нарушения режима остальной части схемы. В результате отключения схема получает вид рис. 25в, в которой пассивный элемент R_k заменен идеаль­ным источником тока J_k=I_k .