Метод законов Кирхгофа

Теоретическая база метода: 1-й и 2-й законы Кирхгофа.

1-й закон Кирхгофа: алгебраическая сумма токов ветвей в узле схемы равна нулю ( ).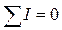

2-й закон Кирхгофа: алгебраическая сумма падений напряжений в произ­вольном кон­туре схемы равна алгебраической сумме ЭДС ( ).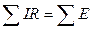

Пусть требуется выполнить расчет режима в заданной сложной схеме (рис. 16) и оп­ределить токи в ветвях, напряжения на отдельных элементах, мощности источников и при­емников энергии. Задана схема цепи и параметры ее отдельных элементов (E₁, E₂, J₁, J₁, J₂, R₁, R₂, R₃, R₄, R₅).

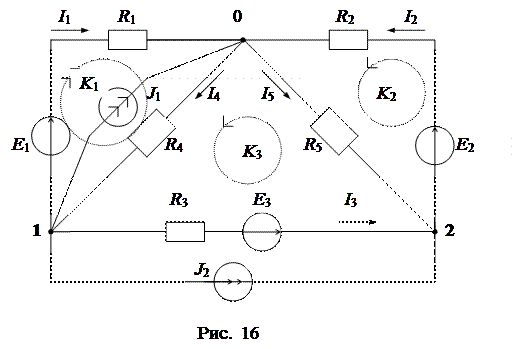Анализируем структуру схемы: схема содержит n=3 (0, 1, 2) узлов и m=5 ветвей с не­определенными токами. В ветвях с источниками тока J токи оп­ре­делены источниками. Об­щее число уравнений должно быть равно числу опре­деляемых токов “m”.

Последовательность (алгоритм) расчета.

1) Задаются (произвольно) положительными направлениями токов в вет­вях схемы (I₁, I₂, I₃, I₄, I₅).

2) Составляется (n-1) уравнений для узлов по первому закону Кирхгофа. Уравнение для последнего n-го узла является зависимым (оно может быть по­лучено путем сложения первых (n-1) уравнений).

3) Не­достающие m-(n-1) уравнений составляются по 2-му закону Кирх­гофа. Пра­вило выбора контуров для составления уравнений: каждый после­дующий контур должен включать в себя хотя бы одну новую ветвь, не охвачен­ную предыдущими уравнениями. Число неза­висимых контуров для схемы лю­бой сложности не может быть больше числа m-(n-1).

Ниже приведена система уравнений Кирхгофа для схемы рис. 16, состоя­щая из m=5 уравнений, из которых n-1=2 составлены для узлов 1 и 2 по 1-му закону Кирхгофа и m-(n-1)=3 составлены для контуров К₁, К₂, К₃ по 2-му за­кону Кирхгофа:

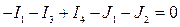- узел 1,

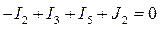- узел 2,

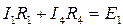- контур К₁,

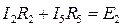- контур К₂,

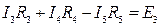- контур К₃.

4) Система уравнений приводится к матричной форме, составляются мат­рицы ко­эф­фициентов:

;

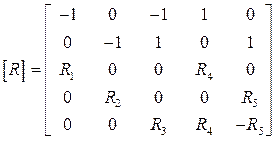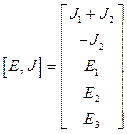
5) Система уравнений решается на ЭВМ по стандартной программе для решения ли­нейных алгебраических уравнений с вещественными коэффициен­тами (SU1), в резуль­тате чего определяются неизвестные токи I₁, I₂, I₃, I₄, I₅. От­рицательные результаты, по­лучаемые для некоторых токов, означают, что их действительные (физические) направ­ления не соот­ветствуют направлениям, принятым в начале расчета.

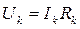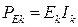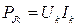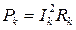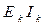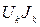6) Определяются напряжения на отдельных элементах схемы ( ), мощно­сти источников ЭДС ( ),источников тока ( ) и прием­ников ( ). При этом мощности приемников энергии всегда положи­тельны, а мощности источников энергии могут быть отрицательными, если со­множители в произведениях и не совпадают по направлению.

4. Метод контурных токов

Теоретическая база метода контурных токов – 2-ой закон Кирхгофа в со­четании с принципом наложения. Предполагают, что в каждом элементарном контуре-ячейке схемы протекает «свой» контурный ток I_k, а действительные токи ветвей получаются по принципу наложения контурных токов как их ал­гебраические суммы. В качестве неизвестных величин, подлежащих определе­нию, в данном методе выступают контурные токи. Общее число неиз­вестных составляет m-(n-1).

Пусть требуется выполнить расчет режима в заданной сложной схеме рис. 11. Пара­метры отдельных элементов схемы заданы.

Последовательность (алгоритм) расчета.

1) Задаются (произвольно) положительными направлениями контурных токов в кон­турах-ячейках схемы(I_к1 , I_к2 , I_к3 ). Контуры-ячейки следует выби­рать так, чтобы они не включали в себя ветви с источниками тока. Ветви с ис­точниками тока J образуют свои кон­туры с заданными токами (J₁, J₂).

2) Составляются m-(n-1) уравнений по 2-му закону Кирхгофа для вы­бранных конту­ров-ячеек с контурными токами I_к1, I_к2, I_к3. В уравнениях учиты­ваются падения напряжений как от собственного контурного тока, так и от смежных контурных токов.

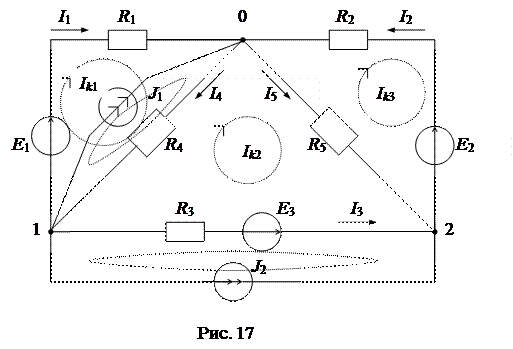Ниже приведена система контурных уравнений для схемы рис. 17:

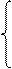
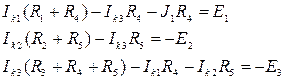
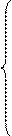В обобщенной форме система контурных уравнений имеет вид:

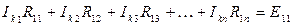
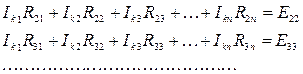
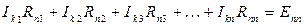
Здесь введены следующие обозначения:

R₁₁= R₁ +R₄; R₂₂ = R₂ +R₅ и т. д. – собственные сопротивления контуров, равные сумме сопротивлений всех элементов контура;

R₁₂ = R₂₁ = 0 ; R₂₃ = R₃₂ = -R₅ и т. д. – взаимные сопротивления между двумя смежными контурами, они положительны – если контурные токи в ветви совпадают, и отрицательны – если контурные токи в ветви направлены встречно, всегда отрицательны – если все контур­ные токи ориентированы оди­наково (например, по часовой стрелке), равны нулю – если кон­туры не имеют общей ветви;

E₁₁ = E₁ + J₁R₄, E₂₂ = -E₂, E₃₃ = - E₃ +J₂R₃ и т. д. – контурные ЭДС, равные алгебраиче­ской сумме слагаемых E_nn = SE + SJR от всех источников контура.

Система контурных уравнений в матричной форме:

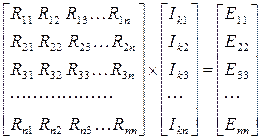или в сокращенно ,

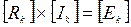где 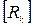- матрица контурных сопротивлений, 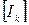- матрица контурных токов, 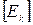- мат­рица контурных ЭДС.

3) Система контурных уравнений решается на ЭВМ по стандартной про­грамме для решения систем линейных алгебраических уравнений с веществен­ными коэффициентами (SU1), в результате чего определяются неизвестные контурные токи I_к1, I_к2, I_к3.

4) Выбираются положительные направления токов в ветвях исходной схемы (рис. 1) (I₁, I₂, I₃, I₄, I₅). Токи ветвей определяются по принципу наложе­ния как алгебраические суммы контурных токов, протекающих в данной ветви.

I₁ = I_к1 - J₁; I₂ = -I_к2; I₃ = -I_к3 – J₂; I₄ = I_к1 – I_k3; I₅ = -I_к2 + I_k3 .

5) При необходимости определяются напряжения на отдельных элемен­тах (U_k = I_kR_k), мощности источников энергии (P_Ek = E_kI_k, P_Jk = U_k J_k) и приемни­ков энергии (P_k = I_k² ×R_k).