Среднее и действующее значения переменного тока и напряжения

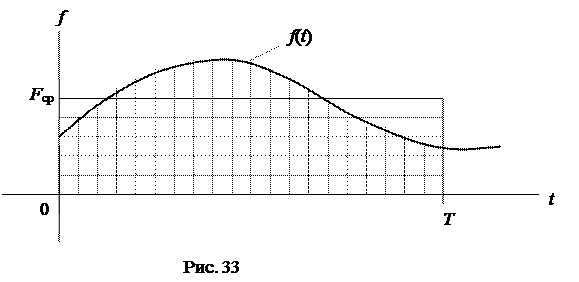
Среднее значение F_ср произвольной функции времени f(t)за интервал времени Т оп­ределяется по формуле :

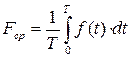
Численно среднее значение F_ср равно высоте прямоугольника, равновели­кого по пло­щади фигуре, ограниченной кривой f(t), осью t и пределами интег­ри­рования 0 – Т (рис. 33).

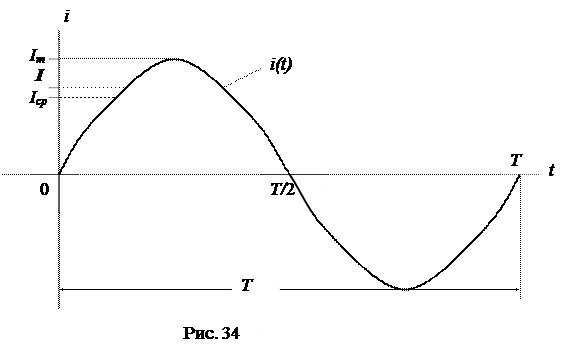
Для синусоидальной функции среднее значение за полный период Т (или за целое число полных периодов) равно нулю, так как площади положи­тельной и отрицательной по­луволн этой функции равны. Для переменного си­нусоидального тока (напряжения) среднее значение определяют за половину периода (Т/2) между двумя нулевыми значениями (рис. 34) :

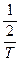
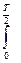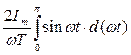
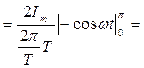
I_ср= I_msinwt dt = 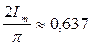I_m

Аналогично получим для напряжения: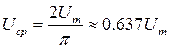

Действующее значение переменного тока (напряжения) определяется как средне­квадратичное значение функции за период :

= = =

= =

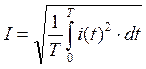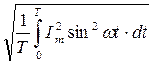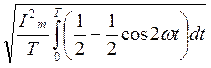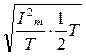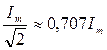
Аналогично получим для напряжения: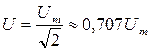

Количество энергии, выделяемое переменным током в резисторе R за время Т, по за­кону Джоуля будет равно W = 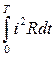=I²RT, а активная мощность соответственно Р = 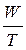= I²R .

Таким образом, параметры электрической энергии на переменном токе (количество энергии, мощность) характеризуются действующими значениями напряжения U и тока I. По этой причине в электроэнергетике принято все тео­ретические расчеты и экспериментальные измерения выполнять для действую­щих значений токов и напряжений. В радиотехнике и в технике связи, наобо­рот, оперируют максимальными значениями этих функций.

Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока. На этом основании можно ут­верждать, что энергетически постоянному току экви­валентно действующее значение пере­менного тока.

Синусоидальная функция времени, как периодическая функция, харак­теризуется следующими коэффициентами :

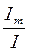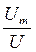
к_а = = 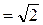» 1,41- коэффициент амплитуды,

к_ф = 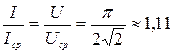– коэффициент формы.