Метод узловых потенциалов
Теоретическая база метода узловых потенциалов – 1-ый закон Кирхгофа в сочетании с потенциальными уравнениями ветвей. В этом методе потенциал одного из узлов схемы принимают равным нулю, а потенциалы остальных (n-1) узлов считают неизвестными, подлежащими определению. Общее число неизвестных составляет (n-1).
Рассмотрим обобщенную ветвь некоторой сложной схемы (рис. 18).
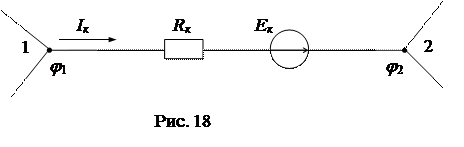 |
Свяжем потенциалы концов ветви (узлов) между собой через падения напряжений на отдельных участках:
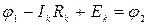 или
или 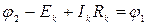
Уравнение, связывающее потенциалы конечных точек ветви через падения напряжений на ее отдельных участках, называется потенциальным уравнением ветви.
Из потенциального уравнения ветви могут быть определены ток ветви и напряжение на резисторе:
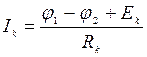 ,
, 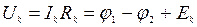 .
.
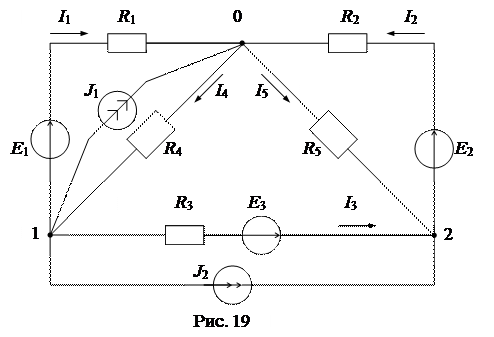
Пусть требуется выполнить расчет режима в заданной сложной схеме рис. 19. Параметры отдельных элементов схемы заданы.
Принимаем потенциал узла 0 равным нулю (j0 = 0), а потенциалы узлов 1 и 2 (j1 и j2) будем считать неизвестными, подлежащими определению.
Зададимся положительными направлениями токов в ветвях схемы I1, I2, I3, I4, I5. Составим потенциальные уравнения ветвей и выразим из них токи ветвей:
I1 = (j1 – j0 + E1 )/ R1
I2 = (j2 – j0 + E2 )/ R2
I3 = (j1 – j0 + E3 )/ R3
I4 = (j0 – j1 )/ R4
I5 = (j0 - j2 )/ R5
 |
Составим (n-1) уравнение по 1-му закону Кирхгофа для узлов 1 и 2:
-I1 – I3 + I4 – J1 – J2 = 0
-I2 + I3 + I5 + J2 =0
Подставим значения токов из потенциальных уравнений в уравнения 1-го закона Кирхгофа. После приведения коэффициентов получим систему узловых уравнений:
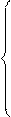 |
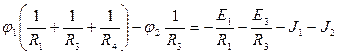
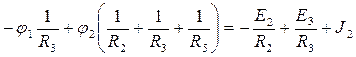
В обобщенной форме система узловых уравнений имеет вид:
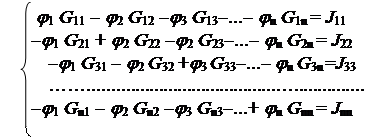 |
Здесь введены следующие обозначения:
G11 =1/R1 +1/R3 +1/R4; G22 =1/R2 +1/R3 +1/R5 и т.д. – собственные проводимости узлов, равные суммам проводимостей всех ветвей, сходящихся в данном узле, всегда положительны;
G12 = G21 = 1/R3; Gnm = Gmn– взаимные проводимости между смежными узлами (1 и 2, m и n), равные сумме проводимостей ветвей, соединяющих эти узлы, всегда отрицательны;
J11 = - E1 /R3 – E3 /R3 – J1; J11 =- E2 /R2 – E3 /R3 + J1 и т.д. – узловые токи узлов, равные алгебраической сумме слагаемых E/R и J от всех ветвей, сходящихся в узле (знак ”+”, если источник действует к узлу, и знак “-” , если источник действует от узла).
Система узловых уравнений в матричной форме:
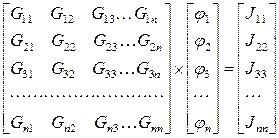 или сокращенно
или сокращенно 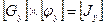 ,
,
где 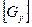 - матрица узловых проводимостей,
- матрица узловых проводимостей, 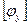 - матрица узловых потенциалов,
- матрица узловых потенциалов, 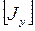 - матрица узловых токов.
- матрица узловых токов.
Последовательность (алгоритм) расчета.
1) Принимают потенциал одного из узлов схемы равным нулю, а потенциалы остальных (n-1) узла считают неизвестными, подлежащими определению.
2) Руководствуясь обобщенной формой, составляют (n-1) уравнение для узлов с неизвестными потенциалами.
3) Определяются коэффициенты узловых уравнений и составляются их матрицы.
4) Система узловых уравнений решается на ЭВМ по стандартной программе для решения систем линейных алгебраических уравнений с вещественными коэффициентами (SU1), в результате чего определяются неизвестные потенциалы узлов j1, j2, …
5) Выбираются положительные направления токов в ветвях исходной схемы I1, I2 , I3, I4, I5. Токи ветвей определяются из потенциальных уравнений ветвей через потенциалы узлов j1, j2, ….
6) При необходимости определяются напряжения на отдельных элементах (Uk = IkRk), мощности источников энергии (PEk = EkIk, PJk = Uk Jk) и приемников энергии (Pk = Ik2 ×Rk).
Метод двух узлов
Метод двух узлов является частным случаем метода узловых потенциалов при числе узлов в схеме n = 2 (рис. 20).
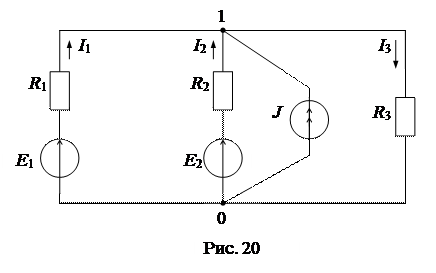
Принимаем j0 = 0, тогда уравнение для узла 1 по методу узловых потенциалов будет иметь вид: j1G11 = J11, откуда следует непосредственное определение напряжения между узлами схемы:
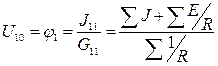 - уравнение метода двух узлов.
- уравнение метода двух узлов.
Применительно к схеме рис. 20 данное уравнение примет конкретную форму:
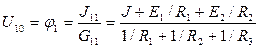
Дата добавления: 2016-10-18; просмотров: 1684;











