Принцип наложения. Метод наложения

Принцип (теорема) наложения гласит, что ток в любой ветви (напряжение на любом элементе) сложной схемы, содержащей несколько источников, равен алгебраической сумме частичных токов (напряжений), возникающих в этой ветви (на этом элементе) от независи­мого действия каждого источника в от­дельности.

Для упрощения доказательства теоремы выберем одну из наружных вет­вей сложной схемы за номером 1, в которой действительный ток равен контур­ному: I₁ = I_k1. Составим для сложной схемы систему контурных уравнений 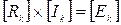и решим ее относительно тока I₁ = I_k1 методом определителей (Крамера):

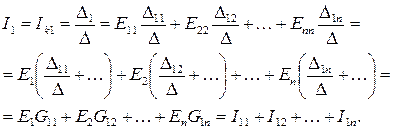
Здесь G₁₁ –входная проводимость ветви 1, G₁₂, G₁₃, …, G_1n– взаимные проводимости между 1-й и остальными ветвями, I₁₁ = E₁G₁₁ – частичный ток в ветви 1 от источника ЭДС E₁, I₁₂ = E₂G_{12, …,} I_1n = E_nG_1n – частичные токи в ветви 1 от источников ЭДС E₂,…, E_n.

Принцип наложения выполняется только для тех физических величин, которые опи­сываются линейными алгебраическими уравнениями, например, для токов и напряжений в линейных цепях. Принцип наложения не выполня­ется для мощности, которая с током связана нелинейным уравнением P=I²×R.

Принцип наложения лежит в основе метода расчета сложных цепей, по­лучившего на­звание метода наложения. Сущность этого метода состоит в том, что в сложной схеме с не­сколькими источниками последовательно рассчиты­ваются частичные токи от каждого источ­ника в отдельности. Расчет частичных токов выполняют, как правило, методом преобразова­ния схемы. Действитель­ные токи определяются путем алгебраического сложения частичных токов с учетом их направлений.

E1 E2

Пример.Задана схема цепи (рис. 21) и параметры ее элементов:E₁ =12 B; E₂ =9 B; R₁= R₂ =R₃ = 2 Ом. Требуется определить токи в ветвях схемы методом наложения.

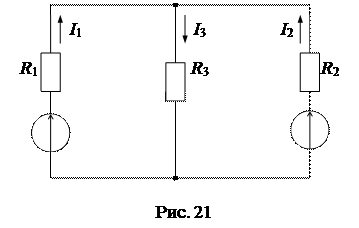
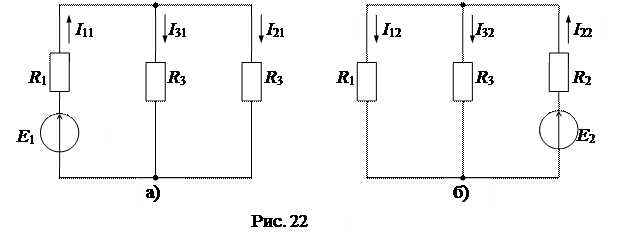
На рис. 22а представлена схема цепи для определения частичных токов от источника ЭДС Е₁, а на рис. 22б - от источника ЭДС Е₂.

Частичные токи в схеме рис. 22а от E₁:

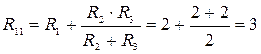Ом; I₁₁= E₁/R₁₁=12/3 = 4A; I₂₁= I₃₁= 2А.

Частичные токи в схеме рис. 22б от E₂:

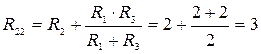Ом; I₂₂ = E₂/R₂₂ = 9/3 = 3A; I₁₂= I₃₂ = 1,5А.

Действительные токи как алгебраические суммы частичных токов:

I₁ = I₁₁ - I₁₂ = 4 – 1,5 = 2,5 A

I₂ = - I₂₁ + I₂₂ = -2 + 3 =1 A

I₃ = I₃₁+ I₃₂ = 2 + 1,5 =3,5 A