Градиентные методы.

Суть всех градиентных методов заключается в использовании вектора градиента для определения направления движения к оптимуму. Вектор градиента

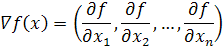
обладает несколькими свойствами, которые обуславливают его эффективное применение при поиске экстремальных значений функции многих переменных. Выделим некоторые из них.

• Вектор градиента всегда направлен в сторону наиболее быстрого возрастания функции в данной точке. Поэтому очевидно, что при поиске минимальных значений функции необходимо двигаться в противоположную сторону. Такое направление движения называют антиградиентом (-∇f(x)) или отрицательным градиентом и оно характеризует направление наиболее быстрого убывания функции.

• Градиент всегда ортогонален линии равного уровня, проходящей через данную точку x^(k).

• Согласно необходимому условию существования экстремума функции многих переменных в точке экстремума градиент функции обращается в ноль. Это свойство часто используется для проверки условия окончания поиска в градиентных методах, т.е.

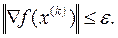
Общий алгоритм всех градиентных методов заключается в построении из некоторой начальной точки x⁽⁰⁾ последовательности приближений (рассматриваем задачу минимизации):

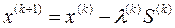(k=0, 1,…),

где S^(k) - единичный вектор в направлении градиента целевой функции f(x)

в точке x^(k):

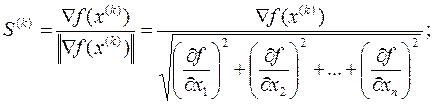
– величина шага в направлении градиента.