Движение в сторону градиента функции.

Промежуточные точки на поверхности отклика рассчитываются по следующей схеме:

.

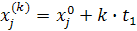Для облегчения вычислений рекомендуется использовать Microsoft Office Excel.

Заполняется следующая таблица:

	Δx1	Δx2	Δx3	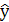(считается по формуле (1))
…	…	…	…

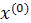
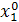
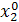
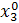
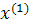
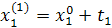
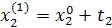
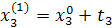
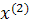
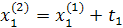
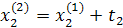
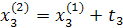
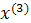
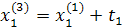
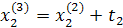
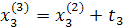
5. Находим экстремальное значение (минимум или максимум). Движение прекращаем, если:

1) найдено экстремальное значение. Определяем максимум это или минимум;

2) определили, что функция монотонна (наибольшее или наименьшее значение функция принимает в начальной точке, а при движении по поверхности отклика постоянно возрастает или же убывает).

Контрольные вопросы.

1. Какие эксперименты называют оптимизационными?

2. Какие методы используют для оптимизации и нахождения экстремума?

3. Принцип метода Гаусса-Зейделя.

4. Метод конфигураций.

5. Симплексные алгоритмы. Разновидности. Отличия.

6. Градиентные методы.

7. Опишите метод крутого восхождения Бокса-Уилсона.

8. Какая задача стояла при выполнении лабораторной работы № 4? Какие выводы можно сделать после выполнения поставленной задачи?

Библиография

1. Ахназарова С. Л., Кафаров В. В. Оптимизация эксперимента в химии и химической технологии: учеб. Пособие для химико-технологических вузов.- М.: Высш. Школа, 1978. – 319 с.

2. Казаков Ю. Б. Методы планирования эксперимента – М.: Энергия, 1971, 7 с.

3. Кринецкий И.И. Основы научных исследований: учеб. пособие для вузов – Киев – Одесса, Вища школа. – Головное изд-во, 1981 – 208 с.

4. Шмитько, Е.И. Процессы и аппараты в технологии строительных материалов и изделий: учебное пособие/ Е.И. Шмитько, Воронеж. гос. арх.- строит. у-т.- Воронеж, 2007.- Т.1 (вопросы теории).-261 с.

5. Методы безусловной многомерной оптимизации: Рек. к выполнению лаб., практ. и курсовых работ/ Сост.: С.А. Шипилов: НФИ КемГУ. – Новокузнецк. 2000.- 31 с.