Метод Нельдера – Мида (деформируемых многогранников).

Данный метод является существенно более эффективным, чем простейший алгоритм регулярных симплексов, за счет того, что симплекс меняет свою форму от цикла к циклу. Рабочий цикл алгоритма состоит из следующих операций [5].

1. Выбирают начальный (обычно регулярный) симплекс x⁽¹⁾ -x⁽²⁾-…- x⁽ⁿ⁺¹⁾

и рассчитывают значения целевой функции в его вершинах.

2. Из найденных значений целевой функции ищут максимальное y_max = f (x_max) и минимальное значение y_min = f (x_min).

3. Отображают «наихудшую» вершину относительно центра тяжести x_ц.т. противоположной грани с коэффициентом α =1.

4. Анализируют результат отображения, сравнивая значение функции в отображенной вершине с ее значениями в вершинах предыдущего симплекса.

a) Если при этом значение функции в новой вершине оказалось меньше, чем наилучшее значение предыдущего симплекса, т.е. y⁽ⁿ⁺²⁾ < y_min , то проводят растяжение симплекса, увеличивая в β>1 (обычно β = 2) раз расстояние от отраженной вершины до центра тяжести x_ц.т.:

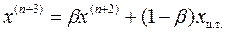(4.1)

Если после операции растяжения значение функции в новой точке уменьшается, т.е. y⁽ⁿ⁺³⁾ < y⁽ⁿ⁺²⁾, то эта вершина принимается за вершину нового симплекса. Если же увеличивается, то в качестве новой вершины берется точка, полученная после отображения y⁽ⁿ⁺²⁾.

b) Когда значение функции в отображенной вершине меньше, чем в наихудшей вершине предыдущего симплекса, но больше, чем во всех остальных, то производят операцию сжатия c коэффициентом β < 1 (обычно β = 0,5) в формуле (4.1).

c) Если значение функции в отображенной точке больше, чем в наихудшей вершине предыдущего симплекса, т.е. y⁽ⁿ⁺²⁾ > y_max , то производят редукцию (уменьшение размеров симплекса обычно в два раза), т.е. координаты всех вершин симплекса сдвигаются на половину расстояния до наилучшей точки

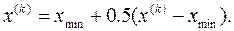
В качестве критерия остановки используют среднеквадратичную величину разности значений функции в вершинах симплекса и среднего ее значения, т.е.

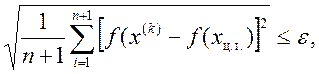
где ε - заданная точность.