Метод крутого восхождения Бокса – Уилсона.
Задача оптимизации методом крутого восхождения по поверхности отклика ставится следующим образом [1]: необходимо определить экспериментально координаты экстремальной точки 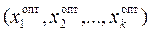 функции
функции 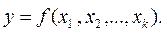 Построим контурные сечения y=const поверхности отклика для k=2 (рис. 4.2, а). При традиционном эксперименте обычно фиксируют один из факторов, например х1, и двигаются из точки L в направлении оси х2. Координаты точки L известны из предварительных опытов. Движение по х2 продолжается до тех пор, пока не прекращается прирост у (рис. 4.2, б).
Построим контурные сечения y=const поверхности отклика для k=2 (рис. 4.2, а). При традиционном эксперименте обычно фиксируют один из факторов, например х1, и двигаются из точки L в направлении оси х2. Координаты точки L известны из предварительных опытов. Движение по х2 продолжается до тех пор, пока не прекращается прирост у (рис. 4.2, б).

Рисунок 4.2 - Движение по поверхности отклика (а) к экстремуму в однофакторном эксперименте и в методе крутого восхождения (б)
В точке с лучшим выходом М фиксируется фактор х2 и начинается движение в направлении оси х1. В точке N снова фиксируется х1 и начинается опять движение по переменной х2 и т.д. Очевидно, что путь к экстремуму по ломаной LMNR не самый короткий. Известно, что движение по кратчайшему, наиболее крутому пути – это движение по градиенту, перпендикулярно линиям y=const (на рис. 4.2, а показано пунктиром). Если описание поверхности отклика в общем случае  градиент функции
градиент функции

где i, j, k – единичные векторы в направлении координатных осей.
Предполагается, что функция f непрерывна, однозначна и не имеет особых точек. Бокс и Уилсон предложили шаговый метод движения по поверхности отклика. В окрестности точки L ставится эксперимент для локального описания поверхности отклика линейным уравнением регрессии:

Далее двигаются по поверхности отклика в направлении градиента линейного приближения:

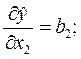 …
… 
При постановке опытов величина шага должна быть пропорциональна произведению коэффициента bj на интервал варьирования bjΔzj. Если одного линейного приближения недостаточно, то ставится новая серия опытов с центром в точке, которая соответствует наибольшему значению у, и находится новое направление для движения по поверхности отклика. Такой шаговый процесс продолжается до достижения области, близкой к экстремуму, или «почти стационарной области».
Направление градиента зависит от выбранного интервала варьирования независимых факторов. При изменении в n раз интервала варьирования для некоторого j-го фактора, меняется в n2 раз величина шага для этого фактора, так как в n раз изменяется коэффициент регрессии bj и также в n раз – интервал варьирования. Инвариантными к изменению интервала остаются только знаки составляющих градиента. Удачный выбор интервала варьирования во многом связан с наличием априорной информации о параметрической чувствительности процесса. Интервал варьирования должен быть достаточно велик, чтобы диапазон изменения выходной величины был в несколько раз (не менее 3-4 раз) больше ошибки воспроизводимости. В то же время для большинства процессов линейное приближение поверхности отклика адекватно эксперименту только при небольших интервалах варьирования. Если на величины интервалов варьирования не наложено никаких ограничений, их стремятся выбрать таким образом, чтобы получить уравнение регрессии, симметричное относительно коэффициентов при линейных членах. Обработка результатов эксперимента, связанного с крутым восхождением, должна сопровождаться тщательным статистическим анализом полученных результатов [1].
Алгоритм поиска.
Пусть мы имеем функцию f(x1, x2). Необходимо найти минимум функции методом крутого восхождения [1].
Выбираем начальную точку поиска  В окрестности точки проводим полный факторный эксперимент ПФЭ 22. Матрица планирования в кодированных переменных для ПФЭ 22 имеет вид:
В окрестности точки проводим полный факторный эксперимент ПФЭ 22. Матрица планирования в кодированных переменных для ПФЭ 22 имеет вид:
| № | Х1 | Х2 | y |
| - 1 | - 1 | y1 | |
| +1 | - 1 | y2 | |
| - 1 | +1 | y3 | |
| +1 | +1 | y4 |
Переход от кодированных переменных к натуральным осуществляется по формуле:
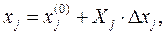 j=1, 2;
j=1, 2;
где 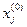 - опорный уровень;
- опорный уровень;
 - кодированное значение переменной;
- кодированное значение переменной;
 - интервал варьирования.
- интервал варьирования.
Опорному уровню соответствуют координаты начальной точки поиска, кодирование значения переменных приведены в матрице ПФЭ 22. Интервал варьирования  для расчетов можно принять равным единице. С учетом этого матрица ПФЭ 22 в натуральных переменных будет иметь вид:
для расчетов можно принять равным единице. С учетом этого матрица ПФЭ 22 в натуральных переменных будет иметь вид:
| № | х1 | х2 | y |
 - 1 - 1
|  - 1 - 1
| y1 | |
 +1 +1
|  - 1 - 1
| y2 | |
 - 1 - 1
|  +1 +1
| y3 | |
 +1 +1
|  +1 +1
| y4 |
Значения y1, y2, y3, y4 определяем, рассчитывая значение функции  для полученных четырех точек. Метод ПФЭ позволяет получить линейную зависимость у от х1 и х2:
для полученных четырех точек. Метод ПФЭ позволяет получить линейную зависимость у от х1 и х2:

Необходимо оценить значения коэффициентов уравнения b1, b2:

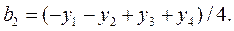
Определив значение коэффициентов регрессии, начинаем движение по поверхности отклика в направлении вектора градиента [-b1, -b2]. Знак «минус» указывает на поиск минимума. Расчет ведем по формуле:

где  - значение j-го фактора на k-том шаге движения в направлении градиента;a – коэффициент пропорциональности (выбираем с учетом предполагаемого вида поверхности отклика).
- значение j-го фактора на k-том шаге движения в направлении градиента;a – коэффициент пропорциональности (выбираем с учетом предполагаемого вида поверхности отклика).
Движение по поверхности отклика осуществляется до тех пор, пока значение функции не начнет увеличиваться. В этом случае за исходную точку берется точка, в которой значение функции будет минимальным. В этой точке вновь реализуется ПФЭ 22, рассчитываются коэффициенты регрессии и вновь осуществляется движение по поверхности отклика. Процедура повторяется до тех пор, пока длина вектора градиента

не станет меньше заданного ε.
Дата добавления: 2021-01-26; просмотров: 629;











