Вероятностные методы. Метод Монте-Карло

В отличие от традиционных численных методов решения задач, заключающихся в разработке алгоритма построения решения, для исследования некоторых классов задач оказывается более целесообразным моделирование их сущности с использованием законов больших чисел теории вероятностей. Оценки f₁, f₂, ... , f_n искомой величины f в этом случае строят на основании статистической обработки материала, полученного в результате многократных случайных испытаний. Основным требованием при этом является сходимость по вероятности рассматриваемой случайной величины к искомому решению задачи:

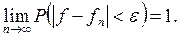(9.1)

Здесь Р – вероятность, ε – сколь угодно малое положительное число.

В отличие от численных методов, описанных ранее, в данном случае вычислительный процесс является недетерминированным. Такой подход к решению вычислительных задач получил общее название метода Монте-Карло. При практической реализации данного подхода случайные величины заменяют сериями, так называемых псевдослучайных величин, генерируемых соответствующими стандартными программами.

9.1. Вычисление определенного интеграла

Пусть задана непрерывная случайная величина ξ (кси), с плотностью вероятности р(х), значения которой распределены на интервале (а, b)

Плотность вероятности р(х) обладает следующими свойствами:

1) p(x) ³ 0;

2) 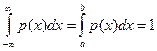. (9.2)

Тогда математическое ожидание случайной величины ξ равно интегралу

M(ξ) = 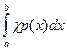. (χ – хи)

Для функции f(ξ), аргументом которой является случайная величина ξ, т. е. для случайной функции, математическое ожидание равно

M(f((ξ)) = 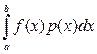. (9.3)

Отсюда следует, что любой интеграл вида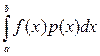

где функция р(х) обладает свойствами (9.2), можно принять за математическое ожидание некоторой случайной функции f(ξ).

Но математическое ожидание случайной величины f(ξ) можно приближенно определить с помощью статистических оценок, т. е. на основе выборки {ξ₁, ξ₂,..., ξ_N} объема N как среднее арифметическое значений {f(ξ₁), f(ξ₂),..., f(ξ_N)} поэтому интеграл (9.3) можно вычислить приближенно по формуле

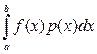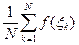» (9.4)

Теоретическим основанием для такого перехода является центральная предельная теорема теории вероятностей, которая в упрощенной формулировке утверждает следующее.

Среднее арифметическое N испытаний случайной величины ξ

ξ_N =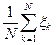

является случайной величиной с тем же математическим ожиданием

M(ξ_N) = М(ξ)

и дисперсией, равной

D(ξ_N) =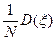

и при N ® ¥ закон распределения случайной величины ξ_N стремится к нормальному закону.

Очевидно, что чем больше N, тем меньше дисперсия D(ξ_N) = 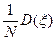. Величину погрешности формулы (9.4)можно оценить по вероятности. Например, при больших N можно утверждать, что с вероятностью 0,997 ошибка не превосходит величину 3σ = 3× 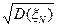(правило «трех сигм» для нормально распределенной случайной величины).

Можно считать, что погрешность формулы (9.4) есть величина порядка O 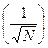, но для повышения точности в данном случае нельзя применять правило Рунге-Ромберга.

Приведем другой способ статистической оценки для одномерного интеграла

.

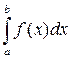Для этого вспомним его геометрический смысл. Предположим, что функция f(x) положительна на отрезке [a, b]. Тогда интеграл равен площади криволинейной трапеции, ограниченной графиком функции f(x), осью абсцисс и прямыми х = а и х = b (рис. 9.1).

Рассмотрим две случайные величины ξ – равномерно распределенную на отрезке [а, b] и η (эта) – равномерно распределенную на отрезке [0, f_max] где f_max = .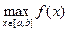

Рис. 9.1

Вероятность попадания случайной точки (ξ, η) в криволинейную трапецию равна отношению площади трапеции к площади прямоугольника

{(х, у), a £ х £ b, 0 £ у £ f_max }:

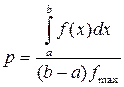(9.5)

Проведем серию из N испытаний и получим N случайных точек (х, у), принадлежащих прямоугольной области {a £ х £ b, 0 £ у £ f_max }. Подсчитаем число N_f точек, удовлетворяющих условию у £ f(x). Тогда вероятность попадания случайной точки (ξ, η) в криволинейную трапецию приближенно равна относительной частоте попадания в криволинейную трапецию, т. е. р » 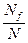и интеграл приближенно вычисляется по формуле

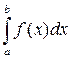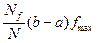» (9.6)

Другой, более простой способ вычисления интеграла заключается в следующем.

Проведем серию из N испытаний случайной величины, равномерно распределенной на отрезке [а, b], и получим N случайных чисел x_i, принадлежащих отрезку [а, b]. Вычислим интеграл по формуле

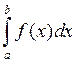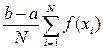» (9.7)

Отметим, что в (9.7) подынтегральная функция может принимать положительные и отрицательные значения, тогда как формула (9.6) применима только для неотрицательной функции f(x).

В общем случае, когда пределы интегрирования могут быть бесконечными, необходимо преобразовать интеграл к виду

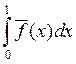(9.8)

и применить формулу (9.7).

9.2. Вычисление кратных интегралов

Метод Монте-Карло для вычисления одномерных интегралов обычно не применяется, так как для получения высокой точности более удобны квадратурные формулы. Этот метод оказывается более эффективным при вычислении кратных интегралов, когда кубатурные формулы для достижения малой погрешности слишком громоздки и требуют большого объема вычислений.

При использовании квадратурных или кубатурных формул, число операций быстро возрастает с ростом размерности интеграла. Например, если для вычисления одномерного интеграла методом трапеций с заданной точностью необходимо вычислить сумму порядка N слагаемых, то для вычисления двойного интеграла тем же методом необходимо сложить порядка N² слагаемых, а для тройного интеграла число слагаемых составляет порядка N³.

Число испытаний N, требующихся для достижения заданной точности ε приближенного значения, в методе Монте-Карло есть величина порядка 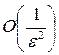и не зависит от размерности интеграла.

Применяется следующий критерий выбора между кубатурной формулой р-го порядка точности и методом Монте-Карло для вычисления с точностью ε кратного интеграла функции m переменных:

1) если число измерений m < 2р, лучше использовать кубатурные или квадратурные формулы;

2) если m > 2р – метод Монте-Карло.

Например, если р = 1, тройные интегралы выгоднее вычислять методом Монте-Карло, а одномерные – квадратурными формулами.

Если р = 2, лучше вычислять методом Монте-Карло пятимерные интегралы, а одномерные, двойные и тройные – квадратурными или кубатурными формулами.

Рассмотрим конкретные формулы метода Монте-Карло для вычисления кратных интегралов, получающиеся способом, который применялся для вывода формулы (9.7).

Пусть требуется вычислить двойной интеграл

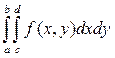. (9.9)

Проведем серию из N испытаний случайной точки (x_i, y_i), где x_i равномерно распределены на отрезке [a, b], a y_i равномерно распределены на отрезке [с, d]. Вычислим интеграл (9.9) по формуле

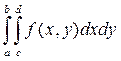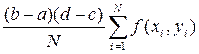= (9.10)

Для тройного интеграла аналогично получим формулу

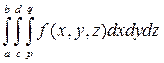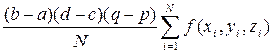= (9.11)

где x_i равномерно распределены на отрезке [a, b], y_i – на отрезке [с, d], a z_i – на отрезке [р, q]; N – число испытаний.

Для m-кратного интеграла формула метода Монте-Карло имеет вид

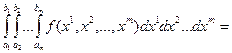
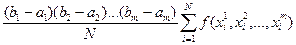. (9.12)

9.3. Решение систем линейных уравнений

Рассмотрим применение метода Монте-Карло для решения системы линейных уравнений

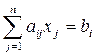, i = 1, ..., n. (9.13)

Пусть система (9.13) приведена к виду

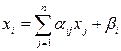, i = 1, ..., n. (9.14)

где норма матрицы α = || a_ij || удовлетворяет условию ||α|| < 1. Тогда система (9.14) имеет единственное решение.

Приведем без доказательства схематическое описание метода Монте-Карло для решения системы линейных уравнений (9.14).

Подберем такие множители v_ij, чтобы решения p_ij уравнений α_ij = p_ij×v_ij удовлетворяли условиям:

1) p_ij ³ 0, причем p_ij > 0, если α_ij ¹ 0;

2) 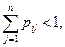i =1, ..., n.

Положим p_i_{, n+1} = l – 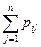, i = 1, ..., n;

p_n_{+1, j}= 0, если j < n + l; p_n_{+1, n+1} = l.

Будем трактовать число p_ij как вероятность перехода некоторой частицы из состояния S_i в состояние S_j. Всего состояний п + 1:

S₁, S₂, ... , S_n₊₁,

причем граничное состояние S_n₊₁ = Г соответствует остановке частицы, так как р_п_+1,_j = 0, т. е. частица не может выйти из состояния S_n₊₁.

Матрица с элементами p_ij называется матрицей перехода состояний {S_i}:

П 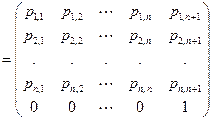. (9.15)

Назовем траекторией T_i совокупность состояний, через которые проходит блуждающая частица, начиная с состояния S_i и заканчивая граничным состоянием Г. Промежуточные состояния частицы обозначим ;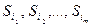

T_i ={ 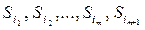= Г }. (9.16)

Поставим в соответствие траектории T_i случайное число X_i:

X_i = β_i + 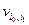× 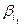+ 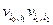× 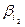+ ××× + 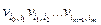× 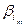, (9.17)

где – свободные члены системы (9.14) с индексами, совпадающими с индексами состояний, образующих траекторию (9.16).

Теорема 9.1. Математические ожидания случайных величин (9.17) равны корням системы (9.14): M(X_i) = x_i, i = 1, ... , п.

Сформулируем алгоритм решения системы линейных уравнений (9.13) методом Монте-Карло.

1. Привести систему (9.13) к виду (9.14):

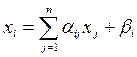, i = 1, ..., n, ||α|| < 1. (9.18)

2. Подобрать такие числа v_ij, чтобы решения p_ij уравнений α_ij = p_ij×v_ij удовлетворяли условиям:

1) p_ij ³ 0, причем p_ij > 0, если α_ij ¹ 0;

2) 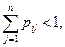i =1, ..., n. (9.19)

Вычислить (п + 1)-й столбец и (п + 1)-ю строку матрицы перехода:

p_i_{, n+1} = l – 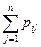, i = 1, ..., n;

p_n_{+1, j}= 0, если j < n + l; p_n_{+1, n+1} = l. (9.20)

3. Выполнить для каждого i = 1, ... , п:

3.0. присвоить значение x_i = 0;

3.1. для каждого k = 1, ... , N (где N число испытаний случайной величины X_i) выполнить статистические испытания по алгоритму:

3.1.0. присвоить m = 0; i_m = i; v = 1; x_i = x_i + β_i;

3.1.1. присвоим переменной очередное значение: m = m + 1;

3.1.2. возьмем случайное число ξ из интервала (0; 1), и выберем значение i_m по следующему правилу:

i_m = 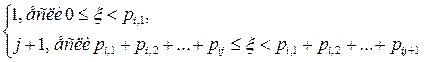, 1 £ j £ n

3.1.3. если j < n + 1, перейти к 3.1.1;

3.1.4. для каждого l = 0, 1, ... , m – 2 вычислить

v = v× 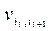, x_i = x_i + v× ;

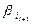3.2. вычислить x_i = x_i / N.

<== предыдущая лекция	\|	следующая лекция ==>
Уравнения в частных производных	\|	Признаки и переменные

Дата добавления: 2020-08-31; просмотров: 717;