Пример выполнения лабораторной работы № 3.

Рассмотрим 3-факторный эксперимент (вариант 3а): N=15, число параллельных опытов m=2 (по приложению 3, таблица 3).

1. Начинаем заполнять предложенную выше таблицу 3.1:

Номер опыта	Экспериментальные значения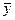
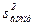
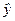
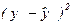
y1	y2
		70,5
		67,5
Сумма столбца	-	-	-		-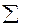

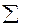
2. Найдем среднее значение отклика :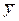

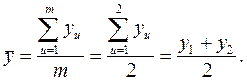
Номер опыта	Экспериментальные значения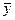
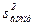
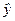
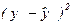
y1	y2
		70,5	70.25
			67.5
		67,5	67.25
			79.5
		66,5	66.25
Сумма столбца	-	-	-		-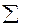

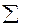
3. Определяем дисперсию воспроизводимости :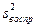

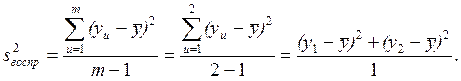
Номер опыта	Экспериментальные значения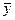
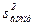
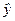
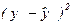
y1	y2
		70,5	70.25	0.125
			67.5	0.5
		67,5	67.25	0.125
			79.5	0.5
		66,5	66.25	0.125
Сумма столбца	-	-	-	3,375	-

Дисперсия воспроизводимости для данного примера равна:

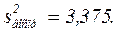
4. Считаем дисперсию коэффициентов.

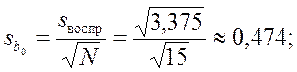
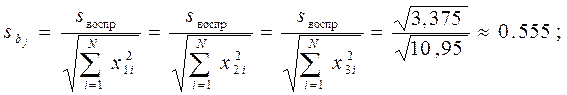
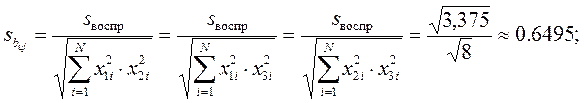
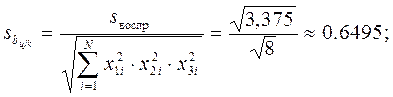
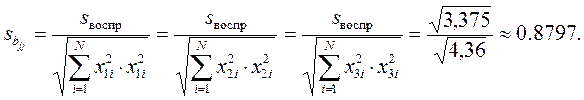
Теперь для каждого коэффициента b_j определяем соответствующее t_j:

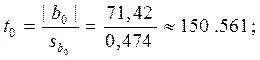
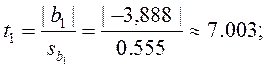
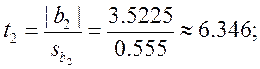
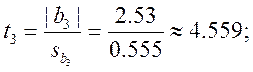
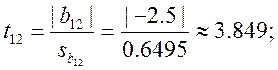
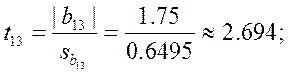
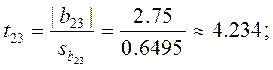
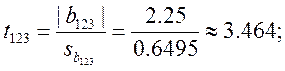
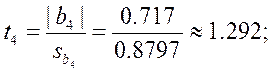
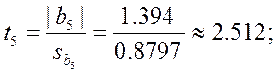
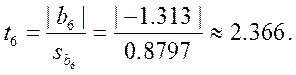
Проверяем значимость коэффициентов.

Уровень значимости:

p=0.05;

и число степеней свободы:

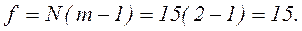
В приложении 2 находим значение соответствующее данному уровню значимости и данной степени свободы:

.

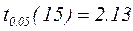Все значения 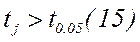являются значимыми.

Значимые: b₀, b₁, b₂, b₃, b₁₂, b₁₃, b₂₃, b₁₂₃, b₅, b₆.

Незначимые: b₄.