Определяем адекватность уравнения регрессии.

5. Из таблицы лабораторной работы № 2 выбираем столбец теоретических значений 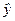. Переносим его в нашу таблицу.

Номер опыта	Экспериментальные значения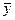
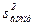
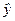
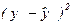
y1	y2
					69.79981191
					68.02438266
					80.84481097
					60.06938173
		70,5	70.25	0.125	70.36169304
			67.5	0.5	66.5862638
					83.4066921
					78.63126286
					77.19986079
		67,5	67.25	0.125	67.75271426
					69.1957804
			79.5	0.5	77.75545426
		66,5	66.25	0.125	66.40320533
					72.55339091
					71.41725078
Сумма столбца	-	-	-	3,375	-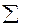

6. Для определения остаточной дисперсии заполняем последний столбец таблицы – находим квадратичную разность 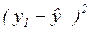в каждой строке.

Номер опыта	Экспериментальные значения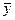
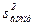
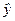
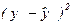
y1	y2
					69.79981191	0.040075273
					68.02438266	0.951829185
					80.84481097	0.713705577
					60.06938173	0.004813824
		70,5	70.25	0.125	70.36169304	0.130821854
			67.5	0.5	66.5862638	0.171177646
					83.4066921	1.978782671
					78.63126286	0.398492799
					77.19986079	3.240501167
		67,5	67.25	0.125	67.75271426	0.566578762
					69.1957804	1.429890763
			79.5	0.5	77.75545426	5.037985569
		66,5	66.25	0.125	66.40320533	0.162574539
					72.55339091	2.092677869
					71.41725078	2.008599766
Сумма столбцов	-	-	-	3,375	-	18.92850727

Теперь по формуле считаем остаточную дисперсию :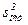

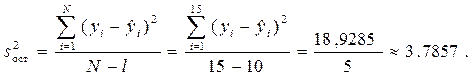
По критерию Фишера:

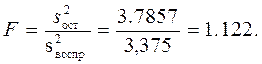
Определим табличное значение критерия Фишера:

Уровень значимости p=0.05;

число степени свободы f₁:

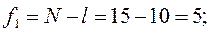
число степени свободы f₂:

.

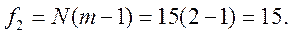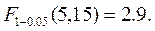
Получаем

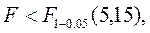
значит уравнение адекватно эксперименту.

Контрольные вопросы.

1. Для чего используют критерий Стьюдента? Приведите схему использования критерия

2. Критерий Кохрена. Формула. Принцип использования.

3. Критерий Фишера (общий случай, одинаковое число опытов).

4. Чем отличается анализ уравнения регрессии, построенного по дробному факторному эксперименту от уравнения регрессии ОЦКП?

5. Как подсчитываются степени свободы для критерия Стьюдента и критерия Фишера?