Если опыты проведены без параллельных, а для получения дисперсии воспроизводимости проделана отдельная серия из m опытов, тогда

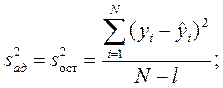
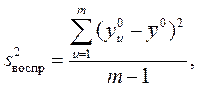
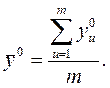
При отсутствии параллельных опытов и дисперсии воспроизводимости можно оценить качество аппроксимации принятым уравнением, сравнив 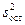и дисперсию относительно среднего :

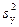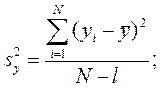
и по критерию Фишера:

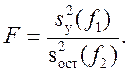
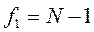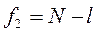В этом случае критерий Фишера показывает, во сколько раз уменьшается рассеяние относительно полученного уравнения регрессии по сравнению с рассеянием относительно среднего. Чем больше значение F превышает табличное F_1-p(f₁, f₂) для выбранного уровня значимости p и чисел степеней свободы и , тем эффектнее уравнение регрессии.

Пример анализа уравнения регрессии для дробного факторного эксперимента [1].

Пусть дана матрица планирования эксперимента.

Но-мер опы-та	x0	x1	x2	x3	x4	x5	x6	x7	y1	y2		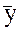s2·104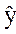
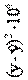
	+1	-1	+1	-1	+1	-1	+1	-1					0,017	2,9
	+1	+1	+1	-1	-1	+1	-1	-1	0,108	0,15	0,129	8,82	0,136	0,49
	+1	-1	-1	-1	-1	+1	+1	+1					0,0088	0,48
	+1	+1	-1	-1	+1	-1	-1	+1	0,194	0,16	0,177	5,78	0,1618	2,3
	+1	-1	+1	+1	-1	-1	-1	+1	0,298	0,292	0,295	1,8	0,2896	0,29
	+1	+1	+1	+1	+1	+1	+1	+1	0,400	0,408	0,404	0,32	0,4086	0,21
	+1	-1	-1	+1	+1	+1	-1	-1	0,255	0,278	0,266	2,6	0,2638	0,073
	+1	+1	-1	+1	-1	-1	+1	-1	0,453	0,408	0,431	10,1	0,4344	0,015

Для определения коэффициентов линейного уравнения регрессии использован дробный факторный эксперимент

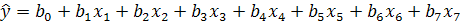
с генерирующими соотношениями

; ; ; .

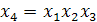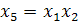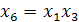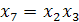Каждый опыт в матрице планирования повторен два раза.

Средние значения параметра 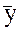получены по двум измерениям. Проверим однородность дисперсий 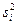, по критерию Кохрена. Сумма дисперсий равна

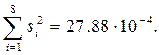
Критерий Кохрена

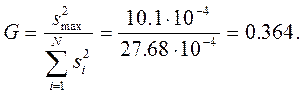
Табличное значение критерия Кохрена для уровня значимости p=0.05 и чисел степеней свободы f₁=1, f₂=8

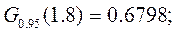
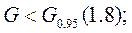
Следовательно, дисперсии однородны. Дисперсия воспроизводимости определяется в связи с этим как средняя арифметическая

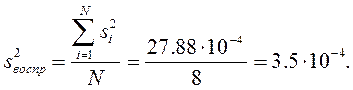
Число степеней свободы дисперсии воспроизводимости равно

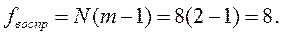
Коэффициенты уравнения регрессии определяем по формуле:

;

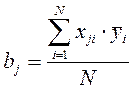и получим

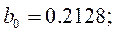
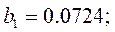
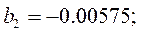
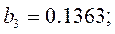
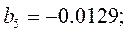
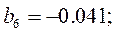
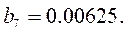
Оценим значимость коэффициентов по критерию Стьюдента. Для этого по формуле:

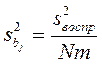
Определим ошибку коэффициентов:

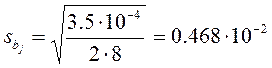
и составим t-отношение для всех коэффициентов уравнения регрессии:

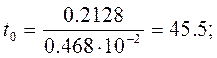
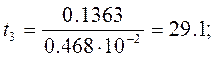
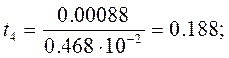
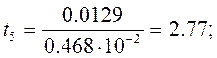
Табличное значение критерия Стьюдента t_0.05(8)=2.31. Коэффициенты b₂, b₄, b₆, b₇ незначимы, так как составленные для них t-отношения меньше табличного. После исключения незначимых коэффициентов уравнение регрессии примет вид:

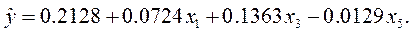
Проверим адекватность этого уравнения эксперименту по критерию Фишера. Дисперсия адекватности определяется по формуле:

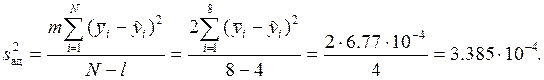
Тогда F-отношение равно

Табличное значение критерия Фишера для p=0.05, f₁=4, f₂=8

F_0.95(4.8)=3.8

F < F_0.95(4.8)

и уравнение регрессии адекватно эксперименту.