Определим значимость коэффициентов регрессии по критерию Стьюдента.

Определяем среднее значение: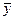

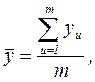
где m – число параллельных опытов, 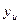- экспериментальное значение отклика, полученное при параллельных опытах. Данные параллельных экспериментов берем из приложения 3.

Так как есть данные о параллельных опытах, то дисперсию воспроизводимости 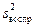можно вычислить по следующей формуле :

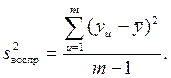
Коэффициенты уравнения регрессии, получаемые при помощи ортогональных планов второго порядка, определяются с разной точностью, поэтому сначала определяем дисперсии коэффициентов по формуле:

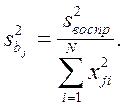
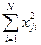- сумма квадратов условного фактора j по i-тому количеству опытов.

Дисперсию коэффициента b₀ можно определить следующим образом:

Дисперсия коэффициента b_j может быть вычислена одним из следующих соотношений:

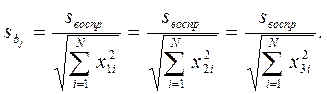
Дисперсия коэффициента b_uj:

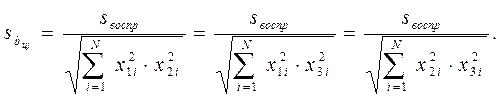
Дисперсия коэффициента b_jj:

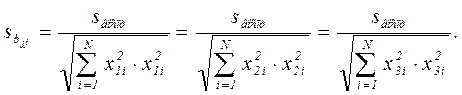
Значимость коэффициентов проверяем по критерию Стьюдента:

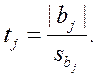
Коэффициент значим, если

.

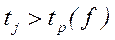f – число степеней свободы дисперсии воспроизводимости:

,

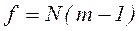N – число опытов в эксперименте; m – число параллельных опытов.

Табличное значение 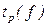определяется с помощью таблицы квантилей распределения Стьюдента при p=0.05(см. приложение). Незначимые коэффициенты можно выбросить из уравнения регрессии.