Обычный симплекс-метод.

Симплексом в пространстве n переменных называют выпуклый многогранник, имеющий n+1 вершину. В пространстве двух переменных это треугольник, в пространстве трех переменных - тетраэдр. В обычном симплекс- методе используется правильный симплекс (все ребра которого равны). Идея симплекс-метода, заключается в следующем.

Выбирается начальный симплекс с вершинами x⁽¹⁾-х⁽²⁾-х⁽³⁾. В вершинах исходного симплекса рассчитывается значение целевой функции f(x⁽¹⁾), f(x⁽²⁾), f(x⁽³⁾). Из этих трех значений выбирается "наихудшая точка (при поиске минимума это та точка, в которой функция принимает максимальное значение). Допустим, что это точка x⁽¹⁾ . Через центр тяжести противолежащей грани x_ц.т.=(x⁽²⁾ + x⁽³⁾)/2 строится новая вершина симплекса x⁽⁴⁾, симметричная "наихудшей" вершине x⁽¹⁾ (рис.4.1):

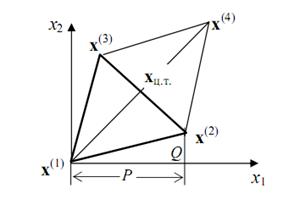
Рисунок 4.1

В результате получается новый симплекс x⁽²⁾ – x⁽³⁾ - x⁽⁴⁾ , причем значение целевой функции в двух точках x⁽²⁾ и x⁽³⁾ уже известно. Поэтому вычисляется значение функции в точке x⁽⁴⁾ и среди всех вершин ищется вершина с «наихудшим» значением. Эта вершина вновь отображается через середину противолежащей грани и вся процедура повторяется. Признаком окончания поиска является так называемая процедура зацикливания, когда вновь отображенная вершина оказывается «наихудшей». В этом случае, если заданная точность не достигается (точность обычно определяется длиной ребра симплекса), необходимо уменьшить размеры симплекса. Процедура повторяется до тех пор, пока длина ребра симплекса не станет меньше заданной точности.

В общем n–мерном случае, если обозначить отображаемую вершину симплекса за x⁽¹⁾, остальные вершины – x⁽²⁾, х⁽³⁾, …, х⁽ⁿ⁺¹⁾ отображенную вершину за x⁽ⁿ⁺²⁾, координаты центра тяжести грани, относительно которой производится отображение, определяются по формуле:

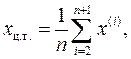
а отображаемой вершины

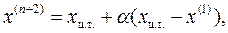
здесь множитель α > 0. При α=1 получаем зеркальное отображение х⁽¹⁾ и если исходный симплекс был правильным, то при зеркальном отображении и новый симплекс окажется правильным.