Взаимосвязь приращений корней и коэффициентов характеристического уравнения

Динамические свойства системы, описываемой уравнением (1), в большой степени определяются корнями характеристического уравнения:

P(p,ak) = pn+ an-1pn-1+ an-2pn-2+…+ a1p + a0= 0 (2.2.2)

При решении уравнения (1) на аналоговой модели погрешности коэффициентов передачи решающих блоков формируют погрешности выставки коэффициентов уравнения (1), а вместе с тем и погрешности в коэффициентах характеристического уравнения (2). Это, в свою очередь, приводит к изменению корней характеристического уравнения, то – есть к изменению динамических свойств моделируемой системы. Для выяснения влияния погрешности выставки параметров аналоговой модели на изменение динамических свойств найдем зависимость малых приращений корней от малых приращений коэффициентов [2.8]. При известных корнях, характеристическое уравнение (2) можно представить ввиде произведения:

P(p,pj) = (p-p1)(p-p2)…(p-pn) = 0 (2.2.3)

Приравняв коэффициенты при одинаковых степенях p в (2) и (3), получим формулы Виета, выражающие коэффициенты характеристического уравнения через его корни :

an-1= -(p1+p2…+pn)

an-2= (p1p2+p1p3+…pn-1pn) (2.2.4)

……………………………

a0= (-1)np1p2…pn

Обратных прямых выражений корней через коэффициенты в общем случае не существует, однако для малых приращений они могут быть получены. Для этого возьмем полные дифференциалы по параметрам akи pjот выражений (2) и (3) соответственно:

dP(p,ak) = = =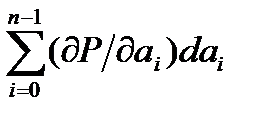

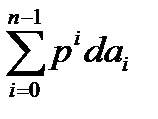= da0+pda1+…+pn-1dan-1 (2.2.5)

dP(p,pj) = 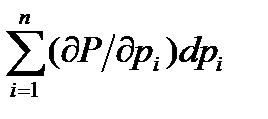= - 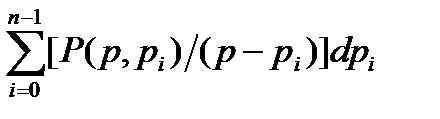(2.2.6)

Для обеспечения равенства полиномов (5) и (6) при любых p

dP(p,ak) = dP(p,pj) (2.2.7)

необходимо и достаточно, чтобы оно выполнялось при n различных значений p. В качестве этих значений удобно выбрать p = pk, k = 1…n. Подставив эти значения в выражение (7) с учетом (5) и (6) получим :

dpk= - (da0+da1pk+…+pkn-1dan-1)/(pk-p1)…

(pk-pk-1)(pk-pk+1)…(pk-pn), k =1,2,…n. (2.2.8)

Таким образом, по формулам Виета (4) можно выразить коэффициенты характеристического уравнения через его корни, а с помощью соотношений (8) - приращения корней через приращения коэффициентов. Последнее позволяет проверить пригодность АВМ для решения определенной задачи.