Обработка и оценка экспериментальных данных.
В результате многофакторного эксперимента получают значения отклика yu в N точках факторного пространства. Для повышения точности экспериментальных данных отклик во многих случаях измеряется несколько раз: ставятся параллельные опыты.
Обработка экспериментальных данных в теории планирования эксперимента в значительной мере формализована, проходит с помощью ЭВМ. Обработка делится на различные этапы, содержащие часто операции условного перехода, допускающие переход к последующему этапу при выполнении некоторого условия. Если условие не выполняется, то вычисления прекращаются, и делаются необходимые изменения в планировании эксперимента. Характер изменений и направление дальнейших действий определяет экспериментатор. Рассмотрим отдельные этапы и возможные варианты неформализованных решений [1].
Для проведения регрессионного анализа примем следующие допущения:
1. Входной параметр x измеряется с пренебрежимо малой ошибкой по сравнению с ошибкой в определении y. Большая ошибка y объясняется наличием в каждом процессе не выявленных переменных, не вошедших в уравнение регрессии.
2. Результаты наблюдений над выходной величиной y1, y2, …, yN представляют собой независимые, нормально распределенные случайные величины.
3. При проведении эксперимента с объемом выборки N при условии, что каждый опыт повторен mi раз, i=1, 2,…,N выборочные дисперсии 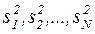 должны быть однородны.
должны быть однородны.
Для исключения явно аномальных, грубых погрешностей, которые могут значительно исказить результаты, в отдельных строках проводится проверка однородности значений yu. Для этого используют критерий Стьюдента [3]:
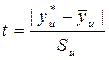 ,
,
где 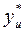 - наименьшее или наибольшее значение отклика в u-той строке, которое полагают ошибочным;
- наименьшее или наибольшее значение отклика в u-той строке, которое полагают ошибочным;  - среднее значение отклика в u-той строке, вычисленной без учета значения
- среднее значение отклика в u-той строке, вычисленной без учета значения 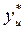 ,
,  - оценка среднего квадратичного отклонения.
- оценка среднего квадратичного отклонения.
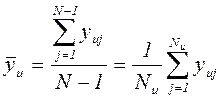 .
.
где 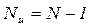 - число опытов без одного, в котором
- число опытов без одного, в котором 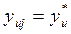 .
.
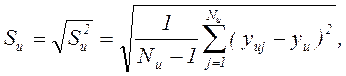
где 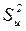 - оценка дисперсии в u-той точке плана без учета сомнительного результата
- оценка дисперсии в u-той точке плана без учета сомнительного результата 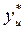 .
.
По таблице распределения критерия Стьюдента (приложение 2) находим значение критерия tт при числе степеней свободы 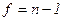 и заданном уровне значимости. Если
и заданном уровне значимости. Если 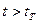 , то значение
, то значение 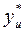 согласуется с данными всей первой строчки и участвует в дальнейших расчетах.
согласуется с данными всей первой строчки и участвует в дальнейших расчетах.
Однородность дисперсий при одинаковом числе степеней свободы проверяют по критерию Кохрена, а при разном – по критерию Бартлета. Определенная по параллельным опытам дисперсия воспроизводимости 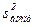 необходима для оценки значимости коэффициентов уравнения регрессии и проверки адекватности уравнения эксперименту.
необходима для оценки значимости коэффициентов уравнения регрессии и проверки адекватности уравнения эксперименту.
Критерий Кохрена:
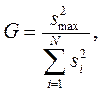
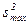 - максимальная дисперсия;
- максимальная дисперсия; 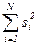 - сумма всех дисперсий.
- сумма всех дисперсий.
Полученное отношение сравнивается с табличным: G1-p(f1, f2), где уровень значимости p=0.05; f1=m-1; m – количество параллельных опытов; f2=N. Если G< G1-p(f1, f2), то дисперсии однородны.
Тогда в качестве оценки для дисперсии воспроизводимости можно взять среднюю дисперсию:
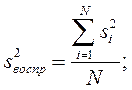
с числом степеней свободы 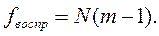
Оценка значимости коэффициентов производится по критерию Стьюдента:
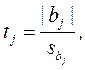
где 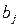 - j-тый коэффициент уравнения регрессии;
- j-тый коэффициент уравнения регрессии; 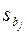 - среднее квадратичное отклонение j-того коэффициента.
- среднее квадратичное отклонение j-того коэффициента.
Если tj больше tp(f) для выбранного уровня значимости p и числа степеней свободы 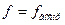 , то коэффициент
, то коэффициент 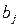 значимо отличается от нуля;
значимо отличается от нуля; 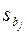 определяется по закону накопления ошибок:
определяется по закону накопления ошибок:
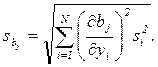
Если выборочные дисперсии 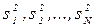 однородны, получим
однородны, получим
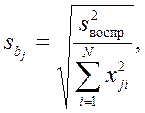
Незначимые коэффициенты исключаются из уравнения регрессии.
Адекватность уравнения проверяется по критерию Фишера:
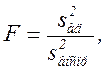
где  - дисперсия адекватности;
- дисперсия адекватности; 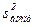 - дисперсия воспроизводимости; F – критериальное значение.
- дисперсия воспроизводимости; F – критериальное значение.
Если критериальное значение F окажется меньше табличного значения F1-p(f1, f2) для уровня значимости p и чисел степеней свободы f1=fад и f2=fвоспр, уравнение адекватно эксперименту.
В общем случае (если каждый опыт повторен mi раз)  и
и 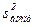 вычисляются следующим образом [1].
вычисляются следующим образом [1].
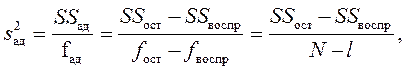
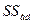 - сумма квадратов адекватности;
- сумма квадратов адекватности;
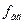 - число степеней свободы дисперсии адекватности;
- число степеней свободы дисперсии адекватности;
l – число значимых коэффициентов в уравнении регрессии;
SSвоспр – сумма квадратов, связанная с дисперсией воспроизводимости 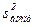 вычисляется следующим образом:
вычисляется следующим образом:
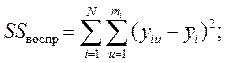
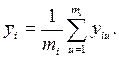
Дисперсия воспроизводимости 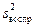 равна:
равна:
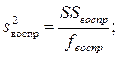
 - число степеней свободы дисперсии воспроизводимости:
- число степеней свободы дисперсии воспроизводимости:

mi – параллельные опыты.
Следовательно, дисперсия воспроизводимости вычисляется как:
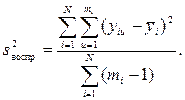
Рассмотрим формулу вычисления остаточной дисперсии  , применяемую при проведении при отсутствии параллельных опытов.
, применяемую при проведении при отсутствии параллельных опытов.
SSост – остаточная сума квадратов:
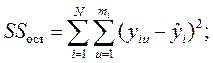
Число степеней свободы остаточной дисперсии  определяется по формуле:
определяется по формуле:
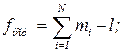
Остаточная дисперсия  :
:
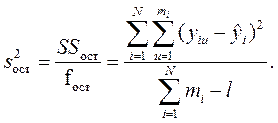
Для одинакового числа опытов m1=m2=…=mi=…=mn=m вычисления упрощаются.
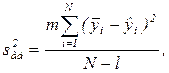
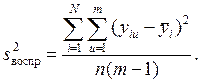
Дата добавления: 2021-01-26; просмотров: 475;











