Самосогласованные уравнения Кона – Шэма и обменно-корреляционная энергия

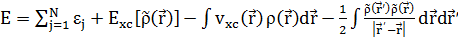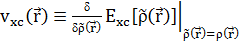В теории метода функционала плотности получено самосогласованное уравнение для энергии основного состояния. Энергия основного состояния определяется как: , где , а 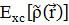– это так называемый функционал обменно-корреляционной энергии, который выбирается в зависимости от системы.

Приближение LDA

Используем приближение однородного электронного газа для неизвестной части функционала энергии. Это приближение называется приближением локальной плотности (local density approximation (LDA)): 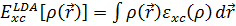, где обозначает обменную и корреляционную составляющие на одну частицу в однородном электронном газе плотности . Соответствующий обменно-корреляционный потенциал тогда имеет вид: и уравнения для орбиталей Кона – Шэма примут вид: .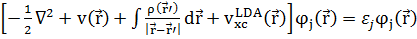

Самосогласованное решение уравнений (#) определяет приближение локальной электронной плотности Кона – Шэма, которое обычно называют просто LDA.

A priori ожидалось, что приближение LDA (очевидно, точное для однородного электронного газа) окажется полезным только в случае плотностей, медленно меняющихся на масштабах порядка локальной фермиевской длины волны 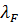и длины волны Томаса – Ферми 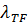. В атомных системах это условие редко выполняется и очень часто серьезно нарушается. Выяснилось, однако, что LDA дает в высшей степени полезные результаты для большинства приложений. Этому нашлось рациональное объяснение (по крайней мере, частичное), когда было замечено, что LDA удовлетворяет правилу сумм, выражающему нормировку обменно-корреляционной (ОК) дырки. Другими словами, при условии, что данный электрон находится в точке 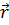, плотность других электронов уменьшается вблизи 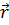по сравнению со средней плотностью 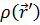; разность представляет собой распределение плотности обменно-корреляционной дырки , интеграл от которой равен 1. Решение уравнений Кона – Шэма в приближении локальной плотности лишь немногим более трудоемко, чем решение уравнений Хартри, и гораздо проще, чем решение уравнений Хартри – Фока. При этом типичная точность расчета обменной энергии КШ — порядка O(10 %), в то же время обычно меньшая по величине корреляционная энергия существенно завышается, как правило, примерно в 2 раза. В большинстве случаев обе ошибки частично сокращаются.

Из практики расчетов известно, что LDA дает энергии ионизации атомов, энергии диссоциации молекул и энергии связи твердых тел с неплохой точностью, обычно 10 – 20%. Несмотря на это, длины связей и, следовательно, геометрическое строение молекул и твердых тел получаются в LDA, как правило, с высокой точностью ~ 1 %.

Приближение локальной плотности, как и приближение локальной спиновой плотности LSDA (local spin density approximation – обобщение LDA для систем с неспаренными спинами), может оказаться непригодным в некоторых случаях, например, для систем с тяжелыми фермионами, когда эффекты электрон-электронного взаимодействия столь сильны, что эти системы теряют всякое сходство с невзаимодействующим электронным газом. [#], [#].

Практическая часть