Метод сильной связи

Исследования дисперсионных свойств углеродных наноматериалов достаточно удобно проводить в рамках метода сильной связи, который хорошо зарекомендовал себя в расчетах систем из легких атомов.

Вследствие трансляционной симметрии кристалла в направлении векторов решетки 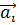любая волновая функция в кристалле должна удовлетворять теореме Блоха

, (i = 1, 2, 3) (1)

где 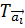– трансляционная операция вдоль вектора решетки, а - волновой вектор. Волновая функция Ψ может быть разложена различными способами. Этот метод имеет определенные преимущества (они просто интегрируемы (иногда и аналитически), точность зависит только от числа использованных плоских волн), но и не лишен недостатков: 1) большой масштаб вычислений, 2) достаточно сложно соотнести плоскую волну и атомную орбиталь в кристалле. Другая форма Ψ, которая удовлетворяет теореме Блоха (1) — линейная комбинация атомных орбиталей (ЛКАО) (в элементарной ячейке или в атоме). Т.е., базисные функции представляются в виде: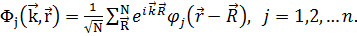

Здесь j – индекс атомной орбитали, – позиция элементарной ячейки, количество волновых функций в элементарной ячейке обозначается как n, что приводит к наличию n волновых функций в кристалле для заданного . N – число элементарных ячеек. Элементарные ячейки взвешиваются фазовым коэффициентом 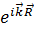. Преимущества данного метода для углеродных структур заключаются в том, что он позволяет: 1) вывести формулы физических свойств, 2) хорошо подходит для легких атомов, 3) число базисных функций n может быть небольшим.

Можно получить квантование вектора в зоне Бриллюэна , p = 0, 1, … M–1. M =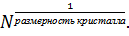

Собственные функции твердого тела описываются линейной комбинацией (ЛК) базисных функций : .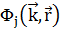

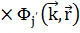Поскольку 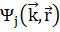должны удовлетворять блоховской теореме (1) суммирование проводится только для одних и тех же 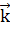. Собственные значения для состояний j даются формулой:

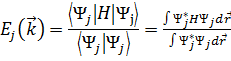, (2)

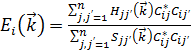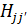где H – гамильтониан в твердом теле. Подставляя (1) в (2) получим: , где и 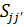называются матрицами переноса и перекрытия соответственно. Минимизацией энергии можно вывести т. н. секулярное уравнение: det[H – ES] = 0, решение которого и дает дисперсионное соотношение.

Таким образом, алгоритм метода сильной связи выглядит следующим образом.

1. Выбрать элементарную ячейку и трансляционные вектора 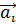. Определить координаты атомов. Выбрать n орбиталей, которые учитываются в расчете.

2. Определить зону Бриллюэна для данной элементарной ячейки и вектора обратной решетки 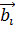. Выбрать характерные точки и направления зоны Бриллюэна.

3. Для каждого k посчитать матрицы и .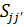

4. Решить секулярное уравнение и найти дисперсионное отношение E(k).