Принцип минимума функционала энергии в терминах волновых функций уравнения Шредингера
Стационарное уравнение Шредингера имеет вид
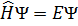 (3)
(3)
где E – энергия электронов, Ψ = Ψ( 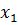 ,
, 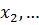
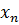 ) – волновая функция системы, а Ĥ – оператор Гамильтона:
) – волновая функция системы, а Ĥ – оператор Гамильтона:
 (4)
(4)
где  – внешний потенциал (в данном случае учитывается только влияние ядер с зарядом α на электрон i). Координаты
– внешний потенциал (в данном случае учитывается только влияние ядер с зарядом α на электрон i). Координаты  включают в себя как пространственные
включают в себя как пространственные 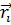 , так и спиновые координаты
, так и спиновые координаты 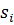 . Можно записать (4) в виде
. Можно записать (4) в виде  , где
, где 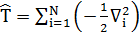 – оператор кинетической энергии,
– оператор кинетической энергии,  – оператор взаимодействия электронов с ядрами, а
– оператор взаимодействия электронов с ядрами, а 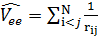 – оператор отталкивания электронов. Общая энергия W записывается в виде W = E + Vnn, где
– оператор отталкивания электронов. Общая энергия W записывается в виде W = E + Vnn, где 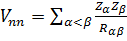 – энергия межъядерного отталкивания. При этом не имеет значения включать ли Vnn в
– энергия межъядерного отталкивания. При этом не имеет значения включать ли Vnn в 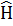 и решать уравнение Шредингера вида
и решать уравнение Шредингера вида 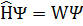 , или решать уравнение ĤΨ = EΨ и добавить Vnn к полученной энергии.
, или решать уравнение ĤΨ = EΨ и добавить Vnn к полученной энергии.
Решения уравнения (3) должны соответствовать определенным граничным условиям. В частности Ψ не должна иметь разрывов и убывать к нулю на больших расстояниях от атома или молекулы или иметь периодическое поведение для бесконечного кристалла. 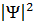 представляет собой распределение вероятности в том смысле, что
представляет собой распределение вероятности в том смысле, что 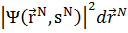 – вероятность обнаружить систему в состоянии с пространственными координатами между
– вероятность обнаружить систему в состоянии с пространственными координатами между 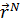 и
и 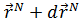 и спиновыми координатами
и спиновыми координатами 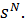 Здесь
Здесь 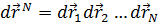 ,
, 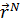 обозначает набор
обозначает набор 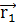 ,
, 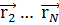 , а
, а 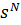 обозначает набор
обозначает набор 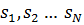 .
.
Существует множество независимых решений (3) Ψk с соответствующими им собственными значениями Ek. Набор Ψk является полным и Ψk могут быть сделаны ортонормированными: 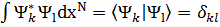 .
.
В дальнейшем, волновая функция основного состояния будет обозначаться 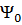 , а энергия E0. Ожидаемые значения кинетической и потенциальной энергий даются как
, а энергия E0. Ожидаемые значения кинетической и потенциальной энергий даются как 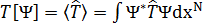 и
и  соответственно. Другими словами они являются функционалами Ψ
соответственно. Другими словами они являются функционалами Ψ 
Предположим, что система находится в состоянии Ψ, которое, возможно, не удовлетворяет уравнению (3). Тогда среднее значение энергии этой системы по множеству измерений дается формулой 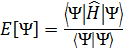 .
.
Поскольку измерения дают одно из собственных значений 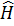 мы получаем
мы получаем 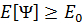 . Энергия, вычисленная из предполагаемой Ψ, является верхней границей для энергии основного состояния
. Энергия, вычисленная из предполагаемой Ψ, является верхней границей для энергии основного состояния 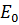 . Полная минимизация функционала E[Ψ] по всем разрешенным волновым функциям даст волновую функцию основного состояния Ψ0 и энергию E[Ψ0] = E0, то есть
. Полная минимизация функционала E[Ψ] по всем разрешенным волновым функциям даст волновую функцию основного состояния Ψ0 и энергию E[Ψ0] = E0, то есть 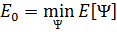 .
.
Дата добавления: 2016-05-31; просмотров: 1600;











