Расчеты зонной структуры углеродных нанотрубок методом сильной связи

В 1992 году было проведено несколько расчетов на основе модели сильной связи для УНТ и графена. Для проведения этих расчетов элементарная ячейка графена была выбрана, как показано на рис. 7, a. В реальном пространстве трансляционные вектора имеют координаты 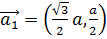, . Вектора же обратной решетки равны .

Рис. 7. Элементарная ячейка и зона Бриллюэна графена.	Рис. 8. Дисперсионное соотношение в графене в модели сильной связи.
В обратной решетке выбрано три характерные точки Г, K и M. Решетка содержит два неэквивалентных атома С. В результате применения метода сильной связи к данной решетке при расчете π – связей было получено следующее выражение:
Рис. 9. Дисперсия в графене с учетом σ – связей.

.

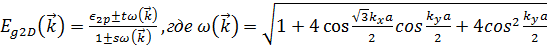Соответствующее дисперсионное соотношение изображено на рис. 8. Если учитывать σ – связи, то можно получить более полное распределение электронов по энергиям (рис. 9).

Для расчета ОУНТ по методу сильной связи были использованы плоская элементарная ячейка (см. рис. 5) и соответствующая ей зона Бриллюэна (рис. #).

В результате расчетов ширины запрещенной зоны углеродных нанотрубок было получено т.н. правило 3k. Согласно этому правилу, УНТ с индексами хиральности (m, n) такими, что |m – n| ≠ 3k (где k – целое) обладают полупроводниковым типом проводимости, тогда как остальные обладают металлической проводимостью или нулевой запрещенной зоной.

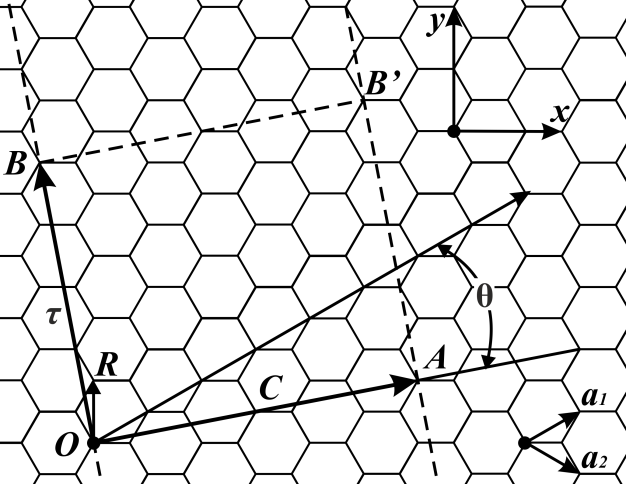
Рис. 10. Элементарная ячейка ОУНТ (4, 2) (C – хиральный вектор, τ – трансляционный вектор).	Рис. 11. Зона Бриллюэна ОУНТ дается отрезком WW’ (для ОУНТ(4, 2)). K1 и K2 – аналоги Ch и T в обратном пространстве.
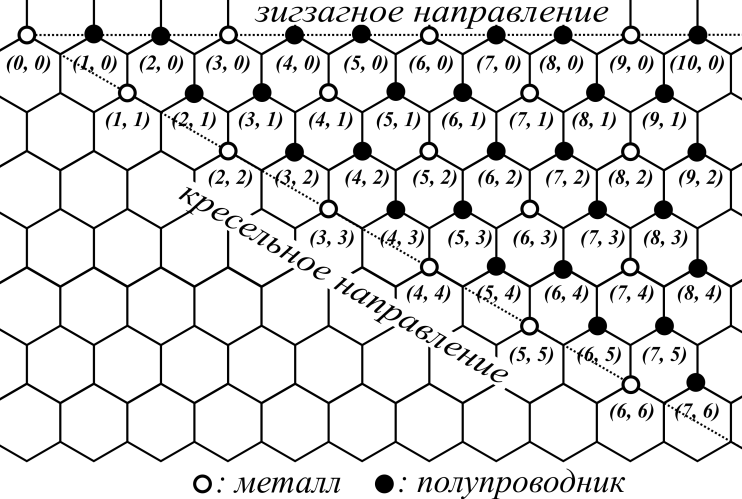
Рис. 12. Данные о запрещенной зоне ОУНТ по методу сильной связи:
а) распределение нанотрубок по типу проводимости (темный значок – полупроводниковая, светлый – металлическая).	б) ширина запрещенной зоны ОУНТ в зависимости от обратного диаметра в единицах интеграла переноса |t| ~ 2.5 эВ.

Итоговые распределения УНТ по типам проводимости в зависимости от хиральности и радиуса приведены на рис. 12 (согласно методу сильной связи без учета эффектов кривизны).