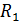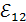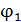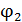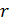Закон Ома. Правила Кирхгофа

Закон Ома для неоднородного участка цепи (рис. 40 а):

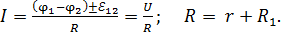(7)

где 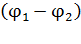– разность потенциалов на концах участка, 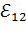– ЭДС (электродвижущая сила) источника тока, 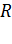– сопротивление участка, 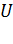– напряжение на участке цепи, – внутреннее сопротивление источника тока.

Для однородного участка цепи (не содержащего источника тока: 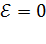) (рис. 40 б) уравнение (37) принимает следующий вид:

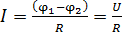. (8)

Для замкнутой цепи (точки цепи 1 и 2 совпадают, следовательно, 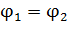) (рис. 40 в) уравнение (7) преобразуется к виду:

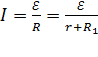, (9)

где 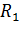– сопротивление внешнего участка цепи, – внутреннее сопротивление источника тока.

Закон Ома в дифференциальной формесвязывает плотность тока 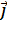в любой точке электрической цепи с напряженностью 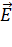электрического поля в этой точке:

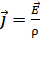. (10)

Правила Кирхгофа используются для расчета разветвленных цепей, содержащих несколько замкнутых контуров.

Первое правило – алгебраическая сумма токов, сходящихся в узле, равна нулю:

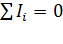. (11)

Здесь положительными считают токи, входящие в узел (приносящие заряд), а отрицательными – выходящие из узла (уносящие заряд).

Второе правило – в любом замкнутом контуре, выбранном в разветвленной электрической цепи, алгебраическая сумма произведений токов 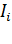на сопротивления 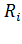на всех участках контура равна алгебраической сумме ЭДС в этом контуре:

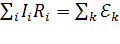. (12)

4.3. Работа и мощность тока. Закон Джоуля– Ленца

Работа по переносу заряда при протекании тока в электрической цепи совершается электростатическим полем в проводнике и сторонними силами, действующими в источнике тока. Работа, совершаемая за время :

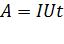, (13)

где 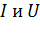– сила тока и напряжение на участке цепи.

Мощность тока 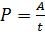; с учетом формулы (13) и закона Ома (7) получают следующие формулы для расчета мощности:

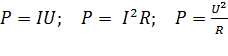. (14)

Закон Джоуля – Ленца: количество теплоты 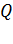, выделяемое в участке цепи за время , определяется следующими формулами:

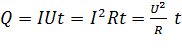. (15)

По закону сохранения энергии 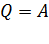– в том случае, если проводник с током неподвижен (сравните формулы (13) и (14) с формулой (15)).