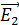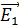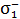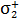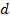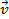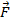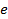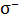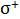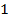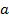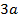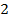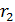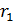Движение заряженных частиц в электростатическом поле
План решения задач
1) Решение задачи следует начать с рисунка, на котором необходимо показать следующее: а) направление силовых линий электростатического поля; б) начальное (точка 1) и конечное (точка 2) положения движущейся заряженной частицы; в) векторы скорости частицы  и силы
и силы 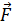 , действующей на частицу с зарядом
, действующей на частицу с зарядом 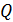 со стороны электрического поля. При этом нужно учитывать, что величина силы
со стороны электрического поля. При этом нужно учитывать, что величина силы
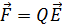 .
.
Из данной формулы следует, что для положительно заряженной частицы (протон, ион 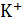 и др.)
и др.) 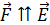 , а для отрицательно заряженного электрона
, а для отрицательно заряженного электрона 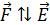 . Если направление силы
. Если направление силы 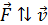 , то движение частицы замедленное, и кинетическая энергия будет уменьшаться при таком движении. Если же сила
, то движение частицы замедленное, и кинетическая энергия будет уменьшаться при таком движении. Если же сила 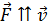 , то частица будет двигаться ускоренно, при этом ее скорость и кинетическая энергия будут возрастать по мере движения.
, то частица будет двигаться ускоренно, при этом ее скорость и кинетическая энергия будут возрастать по мере движения.
2) Так как силы электростатического поля являются консервативными, то для решения задач можно использовать закон сохранения энергии (ЗСЭ). Для этого необходимо выбрать два положения движущейся заряженной частицы в ЭСП и записать в каждом положении полную энергию частицы 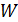 , равную сумме кинетической
, равную сумме кинетической 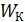 и потенциальной
и потенциальной 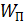 энергии. Затем следует приравнять значения полной энергии частицы в выбранных положениях частицы – в начальном положении 1 и в конечном – 2:
энергии. Затем следует приравнять значения полной энергии частицы в выбранных положениях частицы – в начальном положении 1 и в конечном – 2:
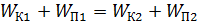 .
.
3) Для величины энергии элементарных частиц нередко используют внесистемную единицу измерения 1 эВ (электрон-вольт). В соответствии с формулой
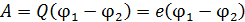 ,
,
энергию величиной 1 эВ приобретает частица, имеющая заряд, равный заряду электрона 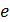 , после прохождения в ЭСП разности потенциалов
, после прохождения в ЭСП разности потенциалов 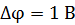 . Следовательно,
. Следовательно,
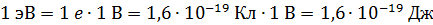 .
.
Таким образом, 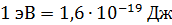 – весьма малая энергия по сравнению с энергией, равной 1 Дж.
– весьма малая энергия по сравнению с энергией, равной 1 Дж.
Задача 15. Электрон с кинетической энергией, равной 20 эВ, движется из бесконечности вдоль силовой линии по направлению к металлической сфере радиусом 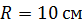 , имеющей потенциал
, имеющей потенциал 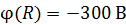 . Определите минимальное расстояние
. Определите минимальное расстояние 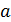 , на которое приблизится электрон к поверхности сферы.
, на которое приблизится электрон к поверхности сферы.
Дано Решение
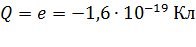 ; ;
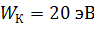 ; ;
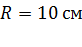 ; ;
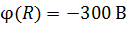 . .
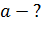
|
|
|
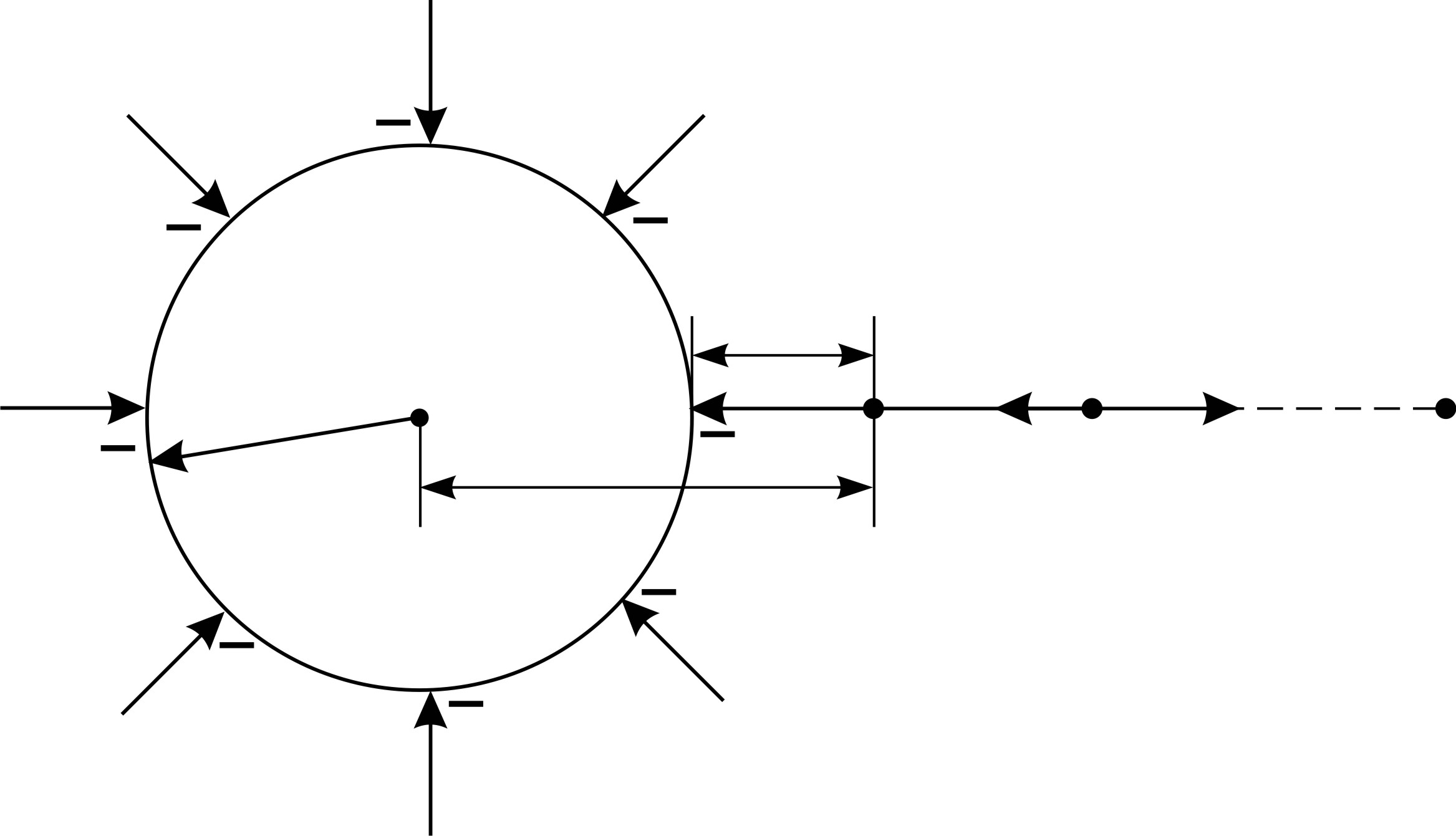
Рис. 31
Так как потенциал сферы 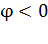 , то сфера имеет отрицательный заряд. При движении электрона (его заряд также отрицательный) к одноименно заряженной сфере на него действует сила отталкивания
, то сфера имеет отрицательный заряд. При движении электрона (его заряд также отрицательный) к одноименно заряженной сфере на него действует сила отталкивания 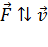 (рис. 31); следовательно, движение электрона будет замедленным. Движение электрона к сфере продолжится до тех пор, когда его скорость, уменьшаясь, станет равной нулю в точке 2 на расстоянии от поверхности сферы, равном
(рис. 31); следовательно, движение электрона будет замедленным. Движение электрона к сфере продолжится до тех пор, когда его скорость, уменьшаясь, станет равной нулю в точке 2 на расстоянии от поверхности сферы, равном  :
: 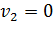 , следовательно, и кинетическая энергия электрона в этой точке
, следовательно, и кинетическая энергия электрона в этой точке 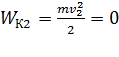 .
.
Благодаря тому, что силы электростатического поля являются консервативными, выполняется закон сохранения энергии – энергия электрона остается постоянной в любой точке ЭСП:
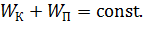 (1)
(1)
Здесь потенциальная энергия 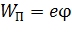 , где
, где  – заряд электрона;
– заряд электрона; 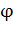 – потенциал поля сферы в той точке, где находится электрон.
– потенциал поля сферы в той точке, где находится электрон.
Определим потенциал поля заряженной сферы, используя формулу связи потенциала ЭСП с его напряженностью:
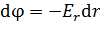 . (2)
. (2)
Здесь проекция на радиальное направление вектора напряженности поля вне сферы 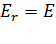 (см. рис. 31). Величина напряженности поля сферы, найденная с помощью теоремы Гаусса:
(см. рис. 31). Величина напряженности поля сферы, найденная с помощью теоремы Гаусса: 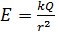 , где
, где 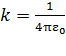 – коэффициент пропорциональности в законе Кулона;
– коэффициент пропорциональности в законе Кулона; 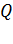 – заряд сферы;
– заряд сферы;  – расстояние от центра сферы до точки, в которой вычисляем значение
– расстояние от центра сферы до точки, в которой вычисляем значение  .
.
Найдем функцию 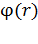 по ее дифференциалу (см. формулу (2)); для этого вычислим неопределенный интеграл:
по ее дифференциалу (см. формулу (2)); для этого вычислим неопределенный интеграл:
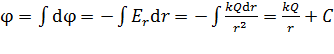 . (3)
. (3)
Константу интегрирования  определим, принимая за нуль потенциал на бесконечно большом расстоянии от сферы:
определим, принимая за нуль потенциал на бесконечно большом расстоянии от сферы: 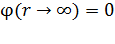 . В соответствии с уравнением (3) запишем:
. В соответствии с уравнением (3) запишем:
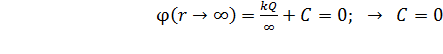 .
.
Тогда потенциал поля, созданного заряженной сферой, на расстоянии  от ее центра
от ее центра
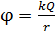 . (4)
. (4)
Соответственно, потенциальная энергия электрона в ЭСП, созданном сферой
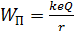 . (5)
. (5)
Заряд сферы 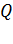 найдем по формуле (4), используя заданный в условии задачи потенциал сферы:
найдем по формуле (4), используя заданный в условии задачи потенциал сферы:
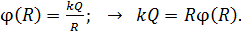 (6)
(6)
Подставляя это выражение в формулу (5), получаем величину потенциальной энергии
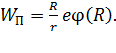 (7)
(7)
Вернемся к уравнению (1) закона сохранения энергии и приравняем энергию частицы в двух точках – 1 и 2 (см. рис. 31):
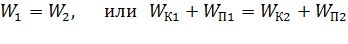 , (8)
, (8)
где 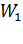 – энергия электрона на бесконечно большом расстоянии от сферы;
– энергия электрона на бесконечно большом расстоянии от сферы; 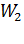 – энергия электрона на минимальном расстоянии от поверхности сферы, равном
– энергия электрона на минимальном расстоянии от поверхности сферы, равном  . Подставим в уравнение (8) величины кинетической и потенциальной энергии электрона в точках 1 и 2:
. Подставим в уравнение (8) величины кинетической и потенциальной энергии электрона в точках 1 и 2:
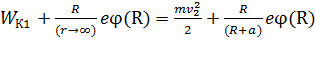 ,
,
или 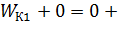
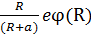 . (9)
. (9)
Таким образом, уравнение ЗСЭ (9) отражает тот факт, что, по мере приближения электрона к одноименно заряженной сфере, его кинетическая энергия переходит в потенциальную энергию взаимодействия электрона с полем сферы. Заметим, что, после остановки электрона на мгновение в точке 2 (на минимальном расстоянии от поверхности сферы), он вновь начнет движение, ускоряясь силой отталкивания  и удаляясь от сферы в радиальном направлении; при этом потенциальная энергия электрона будет уменьшаться, а кинетическая – возрастать, в соответствии с законом сохранения энергии (1).
и удаляясь от сферы в радиальном направлении; при этом потенциальная энергия электрона будет уменьшаться, а кинетическая – возрастать, в соответствии с законом сохранения энергии (1).
Выразим искомое расстояние  из уравнения ЗСЭ (9):
из уравнения ЗСЭ (9):
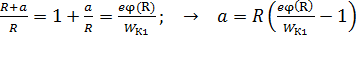 .
.
Вычислим расстояние  электрона от поверхности сферы:
электрона от поверхности сферы:
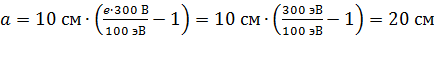 .
.
Таким образом, скорость движения электрона к заряженной сфере в условиях данной задачи уменьшается до нуля на расстоянии 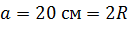 от поверхности сферы.
от поверхности сферы.
Задача 16. Электрон, пройдя в плоском конденсаторе расстояние 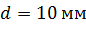 от одной пластины до другой, приобрел скорость
от одной пластины до другой, приобрел скорость 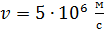 . Найдите 1) разность потенциалов
. Найдите 1) разность потенциалов 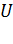 между пластинами и напряженность поля конденсатора, 2) поверхностную плотность заряда на пластинах.
между пластинами и напряженность поля конденсатора, 2) поверхностную плотность заряда на пластинах.
Дано Решение
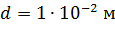 ; ;
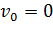 ; ;
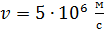 ;
1) ;
1) 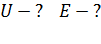 2)
2) 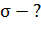
|
|
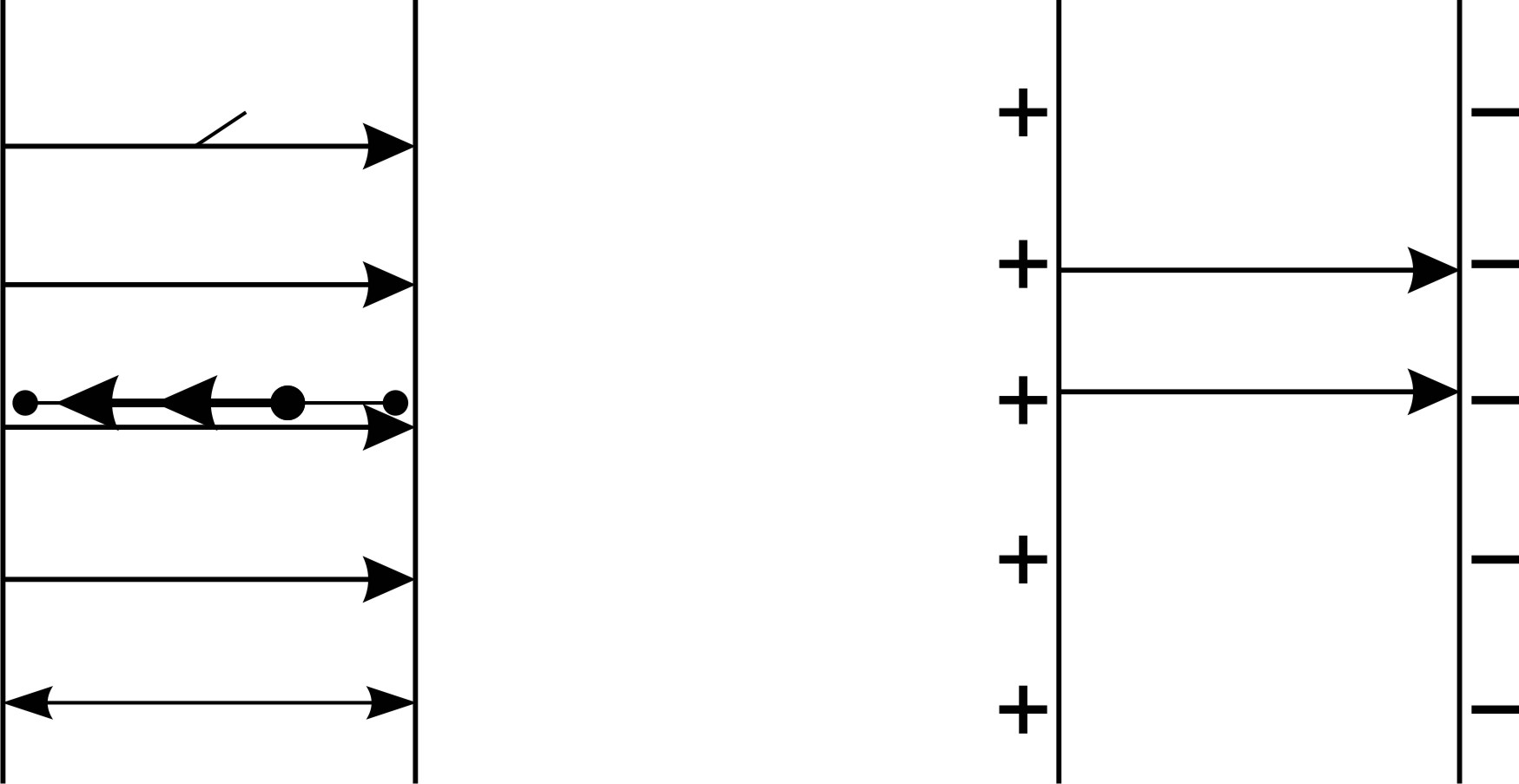
а б Рис. 32 |
1) Линии напряженности 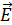 электростатического поля плоского конденсатора перпендикулярны заряженным пластинам. Электрон, ускоряясь силой
электростатического поля плоского конденсатора перпендикулярны заряженным пластинам. Электрон, ускоряясь силой 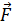 , действующей на него со стороны ЭСП (
, действующей на него со стороны ЭСП ( 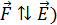 , при движении от точки 1 вблизи отрицательно заряженной пластины до точки 2 на положительно заряженной пластине, приобрел кинетическую энергию
, при движении от точки 1 вблизи отрицательно заряженной пластины до точки 2 на положительно заряженной пластине, приобрел кинетическую энергию 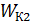 . Так как силы электростатического поля консервативные, то выполняется закон сохранения энергии электрона в следующем виде:
. Так как силы электростатического поля консервативные, то выполняется закон сохранения энергии электрона в следующем виде:
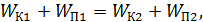 (1)
(1)
где 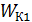 и
и 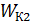 – кинетическая энергия электрона в точках 1 и 2 (рис. 32 а),
– кинетическая энергия электрона в точках 1 и 2 (рис. 32 а), 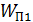 и
и 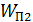 – потенциальная энергия электрона в тех же точках поля конденсатора. Потенциальная энергия заряженной частицы (электрона) в ЭСП описывается формулой:
– потенциальная энергия электрона в тех же точках поля конденсатора. Потенциальная энергия заряженной частицы (электрона) в ЭСП описывается формулой:
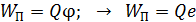 , (2)
, (2)
где 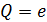 – заряд частицы,
– заряд частицы, 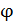 – потенциал той точки поля, в которой находится заряженная частица.
– потенциал той точки поля, в которой находится заряженная частица.
Подставим величины кинетической и потенциальной энергии в уравнение (1) ЗСЭ:
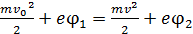 .
.
Перепишем это уравнение с учетом того, что начальная скорость электрона 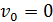 , а разность потенциалов
, а разность потенциалов 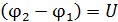 :
:
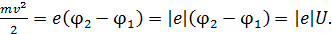 (3)
(3)
Из уравнения (3) определим разность потенциалов между пластинами
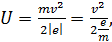 (4)
(4)
где 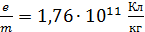 – удельный заряд электрона.
– удельный заряд электрона.
Вычислим разность потенциалов 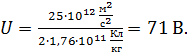
Определим напряженность 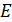 ЭСП конденсатора, учитывая, что это поле однородное и его напряженность, как градиент потенциала, определяется следующей формулой:
ЭСП конденсатора, учитывая, что это поле однородное и его напряженность, как градиент потенциала, определяется следующей формулой:
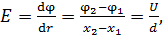 (5)
(5)
где 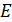 – модуль вектора напряженности;
– модуль вектора напряженности; 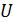 – разность потенциалов между пластинами конденсатора;
– разность потенциалов между пластинами конденсатора; 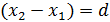 – расстояние между пластинами.
– расстояние между пластинами.
Вычисляем 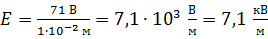 .
.
2) Поверхностная плотность 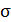 зарядов на пластинах конденсатора определяет величину напряженности поля; установим связь величин
зарядов на пластинах конденсатора определяет величину напряженности поля; установим связь величин 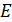 и
и 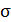 . Напряженность ЭСП внутри плоского конденсатора, в соответствии с принципом суперпозиции, равна сумме векторов напряженности полей первой и второй пластин (рис. 32 б):
. Напряженность ЭСП внутри плоского конденсатора, в соответствии с принципом суперпозиции, равна сумме векторов напряженности полей первой и второй пластин (рис. 32 б):
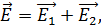 (6)
(6)
где вектор 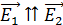 , а модуль напряженности полей, созданных первой и второй пластинами конденсатора, определяется формулами, полученными с помощью теоремы Гаусса:
, а модуль напряженности полей, созданных первой и второй пластинами конденсатора, определяется формулами, полученными с помощью теоремы Гаусса:
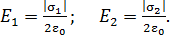 (7)
(7)
Так как заряды и поверхностные плотности зарядов пластин конденсатора одинаковы: 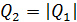 и
и 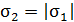 , то, согласно формулам (7), одинаковы и напряженности полей:
, то, согласно формулам (7), одинаковы и напряженности полей: 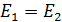 . Тогда, по принципу суперпозиции (6), модуль напряженности ЭСП в плоском конденсаторе
. Тогда, по принципу суперпозиции (6), модуль напряженности ЭСП в плоском конденсаторе
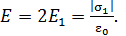 (8)
(8)
Из этого выражения получаем расчетную формулу поверхностной плотности заряда на пластинах конденсатора и вычисляем значение 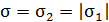 :
:
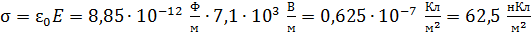 .
.
Задача 17. Электростатическое поле создано бесконечной прямой нитью, заряженной с линейной плотностью заряда 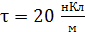 . Определите кинетическую энергию электрона
. Определите кинетическую энергию электрона 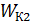 в точке 2, если в точке 1 его кинетическая энергия
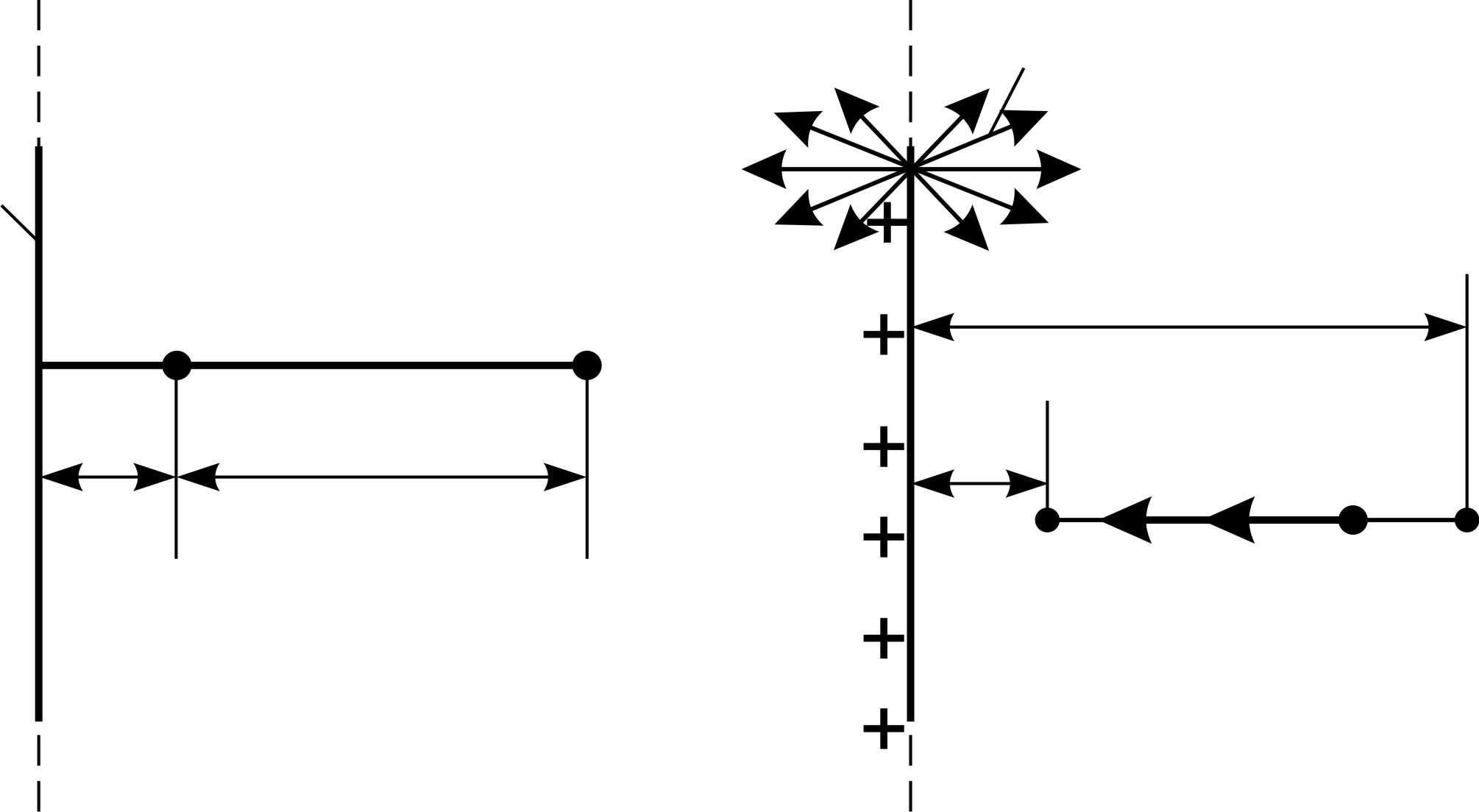
в точке 2, если в точке 1 его кинетическая энергия 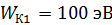 . Расстояния, задающие положения точек 1 и 2 в ЭСП, показаны на рис. 33 а.
. Расстояния, задающие положения точек 1 и 2 в ЭСП, показаны на рис. 33 а.
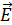
|
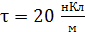 ;
электрон: ;
электрон: 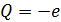 ; ;
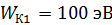 ; ;
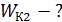
|
а б Рис. 33 |
Электростатическое поле, созданное заряженной нитью, имеет радиально направленные силовые линии (рис. 33 б) и имеет осевую симметрию (ось симметрии поля – заряженная нить). Напряженность такого поля в точке на расстоянии 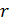 от нити, вычисленная с помощью теоремы Гаусса, определяется формулой
от нити, вычисленная с помощью теоремы Гаусса, определяется формулой
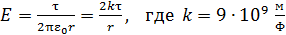 . (1)
. (1)
Движение электрона из точки 1 в точку 2 по направлению к положительно заряженной нити будет ускоренным; оно происходит под действием силы 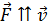 :
: 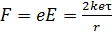 . Эта сила будет возрастать по мере движения электрона вследствие уменьшения расстояния
. Эта сила будет возрастать по мере движения электрона вследствие уменьшения расстояния 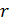 от нити. Описание движения частицы под действием переменной силы потребует составления и решения закона динамики движения в дифференциальной форме с последующим интегрированием, что является непростой задачей.
от нити. Описание движения частицы под действием переменной силы потребует составления и решения закона динамики движения в дифференциальной форме с последующим интегрированием, что является непростой задачей.
Существует рациональный путь решения задачи с помощью закона сохранения энергии, который выполняется благодаря консервативности сил электростатического поля. Запишем формулировку ЗСЭ:
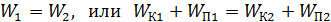 , (2)
, (2)
где 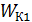 и
и 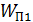 – кинетическая и потенциальная энергии электрона в точке 1 (см. рис. 33 б);
– кинетическая и потенциальная энергии электрона в точке 1 (см. рис. 33 б); 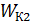 и
и 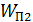 – те же величины в точке 2 ЭСП конденсатора.
– те же величины в точке 2 ЭСП конденсатора.
Из уравнения (2) выразим определяемую величину кинетической энергии электрона
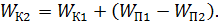 (3)
(3)
Потенциальная энергия частицы с зарядом 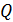 в точке поля, имеющей потенциал
в точке поля, имеющей потенциал 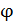 , описывается следующей формулой:
, описывается следующей формулой:
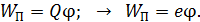 (4)
(4)
С учетом формулы (4) расчетная формула (3) преобразуется к виду:
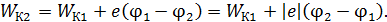 (5)
(5)
Вычислим разность потенциалов ( 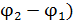 в ЭСП, созданном заряженной нитью. Для этой цели используем формулу связи между напряженностью и потенциалом в виде
в ЭСП, созданном заряженной нитью. Для этой цели используем формулу связи между напряженностью и потенциалом в виде 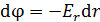 :
:
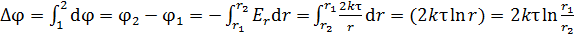 . (6)
. (6)
Подставим полученную разность потенциалов в выражение (5), которое при этом преобразуется к следующему виду:
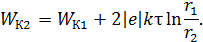
По полученной расчетной формуле вычислим кинетическую энергию электрона в точке 2, выражая начальную энергию электрона в джоулях ( 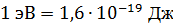 ):
):
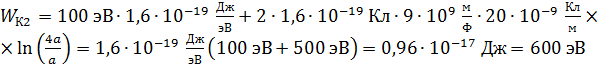 .
.
Дата добавления: 2016-10-07; просмотров: 3241;