Пример решения задач про сопротивления.
Задача 21. При измерении мультиметром постоянного напряжения в диапазоне до 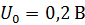 сопротивление прибора
сопротивление прибора 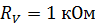 . Какие сопротивления
. Какие сопротивления 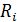 используются в приборе и как они подсоединяются к сопротивлению
используются в приборе и как они подсоединяются к сопротивлению 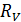 для переключения диапазона измерений на
для переключения диапазона измерений на  , равные 2; 20; 200 и 600 В?
, равные 2; 20; 200 и 600 В?


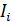
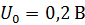 ;
; 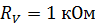 ;
; 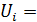 2; 20; 200; 600 В.
2; 20; 200; 600 В. 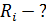
V

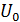
V

а б
Рис. 42
При подключении мультиметра на напряжение 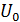 через прибор протекает ток
через прибор протекает ток  (рис. 42 а); величина его, в соответствии с законом Ома:
(рис. 42 а); величина его, в соответствии с законом Ома:
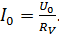 (1)
(1)
Значение  является наибольшим допустимым для данного прибора. При подключении этого мультиметра на напряжение в большем диапазоне
является наибольшим допустимым для данного прибора. При подключении этого мультиметра на напряжение в большем диапазоне  ток, согласно формуле (1), возрастал бы. Чтобы снизить его до
ток, согласно формуле (1), возрастал бы. Чтобы снизить его до 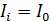 , необходимо увеличить сопротивление цепи. Это делают путем подключения последовательно к сопротивлению
, необходимо увеличить сопротивление цепи. Это делают путем подключения последовательно к сопротивлению  (сопротивлению прибора на минимальном диапазоне) добавочного сопротивления
(сопротивлению прибора на минимальном диапазоне) добавочного сопротивления  (рис. 42 б); при этом ток в цепи, согласно закону Ома:
(рис. 42 б); при этом ток в цепи, согласно закону Ома:
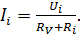 (2)
(2)
Приравнивая максимальный ток, идущий через прибор, определяемый формулами (1) и (2), получаем формулу для расчета величины добавочного сопротивления 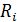 :
:
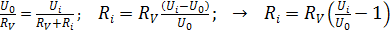 . (3)
. (3)
Вычисляем величины добавочных сопротивлений 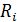 для заданных диапазонов измеряемых напряжений
для заданных диапазонов измеряемых напряжений  по формуле (3):
по формуле (3):
Для 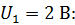
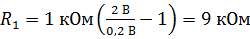 ;
;
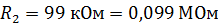 ;
; 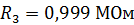 ;
;
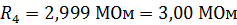 .
.
Задача 22. При измерении мультиметром постоянного тока в диапазоне до 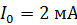 сопротивление прибора
сопротивление прибора 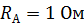 . Какие сопротивления
. Какие сопротивления 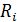 используются в приборе и как они подключаются к сопротивлению
используются в приборе и как они подключаются к сопротивлению 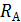 при переключении диапазона измерений на токи
при переключении диапазона измерений на токи 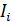 , равные 20; 200 мА и 10 А?
, равные 20; 200 мА и 10 А?

Дано Решение
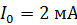 ;
; 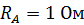 ;
; 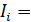 20; 200 мА; 10 А.
20; 200 мА; 10 А. 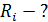
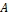
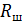
В
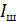
А
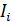
А


а б
Рис. 43
При использовании мультиметра в режиме работы амперметра с диапазоном измеряемых токов до 2 мА через прибор может протекать максимальный ток  (рис. 43 а), равный, в соответствии с законом Ома:
(рис. 43 а), равный, в соответствии с законом Ома:
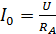 . (1)
. (1)
Значение  является наибольшим из допустимых значений тока для данного прибора. Чтобы измерять этим мультиметром ток большего диапазона
является наибольшим из допустимых значений тока для данного прибора. Чтобы измерять этим мультиметром ток большего диапазона 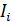 , необходимо часть тока, равную (
, необходимо часть тока, равную ( 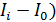 , отвести в другую ветвь электрической цепи (рис. 43 б). Сопротивление
, отвести в другую ветвь электрической цепи (рис. 43 б). Сопротивление 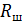 этой ветви называют шунтирующим сопротивлением (или кратко – шунт). При этом через прибор будет протекать ток, равный
этой ветви называют шунтирующим сопротивлением (или кратко – шунт). При этом через прибор будет протекать ток, равный  – максимальный при измеряемом токе, равном верхней границе диапазона
– максимальный при измеряемом токе, равном верхней границе диапазона 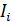 , или кратный
, или кратный  – при измеряемых токах, меньших значения
– при измеряемых токах, меньших значения 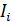 . Таким образом, шунтирующее сопротивление подключают параллельно сопротивлению прибора
. Таким образом, шунтирующее сопротивление подключают параллельно сопротивлению прибора 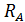 на минимальном диапазоне.
на минимальном диапазоне.
Соотношение токов  (через сопротивление
(через сопротивление 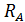 ) и
) и 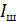 (через шунт) найдем, записывая второе правило Кирхгофа для замкнутого контура электрической цепи (см. рис. 43 б), выбрав направление обхода контура – по часовой стрелке:
(через шунт) найдем, записывая второе правило Кирхгофа для замкнутого контура электрической цепи (см. рис. 43 б), выбрав направление обхода контура – по часовой стрелке:
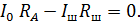 (2)
(2)
Здесь в правой части уравнения записан нуль, так как в контуре нет ЭДС источника тока.
Из уравнения (2) выразим искомое сопротивление шунта
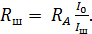 (3)
(3)
Соотношение между током 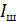 и измеряемым током
и измеряемым током 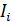 найдем, используя первое правило Кирхгофа для узла
найдем, используя первое правило Кирхгофа для узла 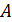 электрической цепи (см. рис. 43 б):
электрической цепи (см. рис. 43 б):
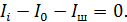 (4)
(4)
Величины 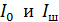 в сумме токов взяты со знаком «минус», так как эти токи уносят заряд из узла
в сумме токов взяты со знаком «минус», так как эти токи уносят заряд из узла 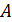 , в отличие от тока
, в отличие от тока 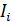 , приносящего заряд в узел
, приносящего заряд в узел 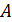 электрической цепи.
электрической цепи.
Величину тока 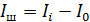 , согласно уравнению (4), подставим в формулу (3) и получим следующую расчетную формулу:
, согласно уравнению (4), подставим в формулу (3) и получим следующую расчетную формулу:
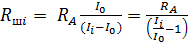 . (5)
. (5)
Из последней формулы следует, что сопротивление 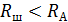 , так как большую часть измеряемого тока нужно отвести в параллельную шунтирующую ветвь.
, так как большую часть измеряемого тока нужно отвести в параллельную шунтирующую ветвь.
Вычисляем сопротивления шунтов по формуле (5):
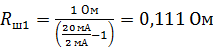 ;
; 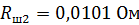 ;
;
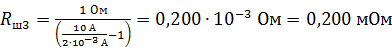 .
.
Заметим, что шунтирование в электрических цепях применяется в электротехнических устройствах, а также бывает в электрической дуге, в частности, в дуговом газовом разряде, который применяется для сварки металлов, и в электродуговой печи для получения легированной стали.
Задача 23. Допустимая рабочая величина плотности тока для медного проводника 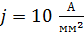 . Определите при данном токе следующие величины: 1) напряженность
. Определите при данном токе следующие величины: 1) напряженность 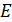 электрического поля в этом проводнике; 2) напряжение
электрического поля в этом проводнике; 2) напряжение 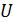 на концах проводника длиной
на концах проводника длиной 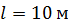 и площадью поперечного сечения
и площадью поперечного сечения 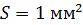 ; 3) мощность
; 3) мощность 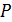 , которая выделяется в этом проводнике.
, которая выделяется в этом проводнике.
Дано Решение
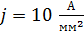 ;
; 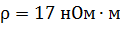 ;
; 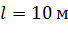 ;
; 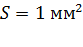 .
. 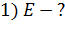 2)
2) 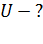
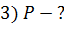
1) Плотность тока  в проводнике зависит от напряженности
в проводнике зависит от напряженности  электрического поля, которое имеется в каждой точке проводника при протекании в нем тока, в соответствии с законом Ома в дифференциальной форме:
электрического поля, которое имеется в каждой точке проводника при протекании в нем тока, в соответствии с законом Ома в дифференциальной форме:
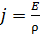 , (1)
, (1)
где  – удельное сопротивление материала проводника.
– удельное сопротивление материала проводника.
Из формулы закона (1) получаем расчетную формулу напряженности электрического поля в проводнике:
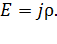
Вычисляем величину

2) Считая, что электрическое поле внутри однородного проводника является однородным, используем для этого квазистатического поля формулу связи напряженности с разностью потенциалов, как для электростатического поля, в следующем виде:
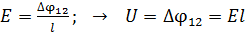 . (2)
. (2)
Вычисляем напряжение, равное разности потенциалов на концах однородного участка цепи, по формуле (2):
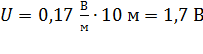 .
.
3) Электрическую мощность, которая выделяется в проводнике, можно рассчитать по формуле закона Джоуля – Ленца:
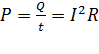 .
.
Заменяя в этой формуле ток, в соответствии с законом Ома:  , получаем расчетную формулу величины мощности:
, получаем расчетную формулу величины мощности:
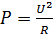 , (3)
, (3)
где 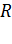 – сопротивление проводника; для однородного проводника с постоянным сечением
– сопротивление проводника; для однородного проводника с постоянным сечением  справедлива формула
справедлива формула
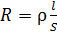 . (4)
. (4)
Выполним расчет по формуле (4), чтобы оценить порядок величины электрического сопротивления таких проводников, используемых, в частности, в бытовой технике:
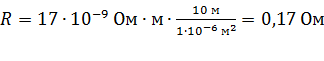 .
.
Вычисляем по формуле (3) электрическую мощность, выделяемую в проводнике при протекании в нем тока:
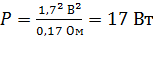 .
.
Задача 24. При подключении сопротивления 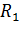 к источнику тока в нем протекает ток
к источнику тока в нем протекает ток 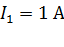 и на этом сопротивлении выделяется мощность
и на этом сопротивлении выделяется мощность 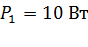 , а при другой величине внешнего сопротивления, равной
, а при другой величине внешнего сопротивления, равной 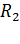 , ток в цепи
, ток в цепи 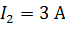 и на сопротивлении
и на сопротивлении 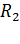 выделяется мощность
выделяется мощность 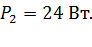 Определите следующие величины: 1) внутреннее сопротивление источника тока
Определите следующие величины: 1) внутреннее сопротивление источника тока  ; 2) ЭДС источника тока
; 2) ЭДС источника тока  ; 3) ток короткого замыкания источника тока
; 3) ток короткого замыкания источника тока 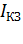 ; 4) КПД источника тока при двух сопротивлениях внешней цепи, равных
; 4) КПД источника тока при двух сопротивлениях внешней цепи, равных 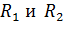 .
.
Дано Решение
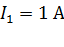 ;
; 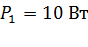 ;
; 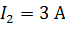 ;
; 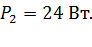
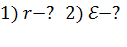 3)
3) 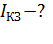
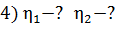
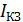
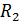
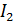
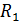
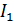
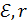
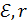
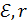
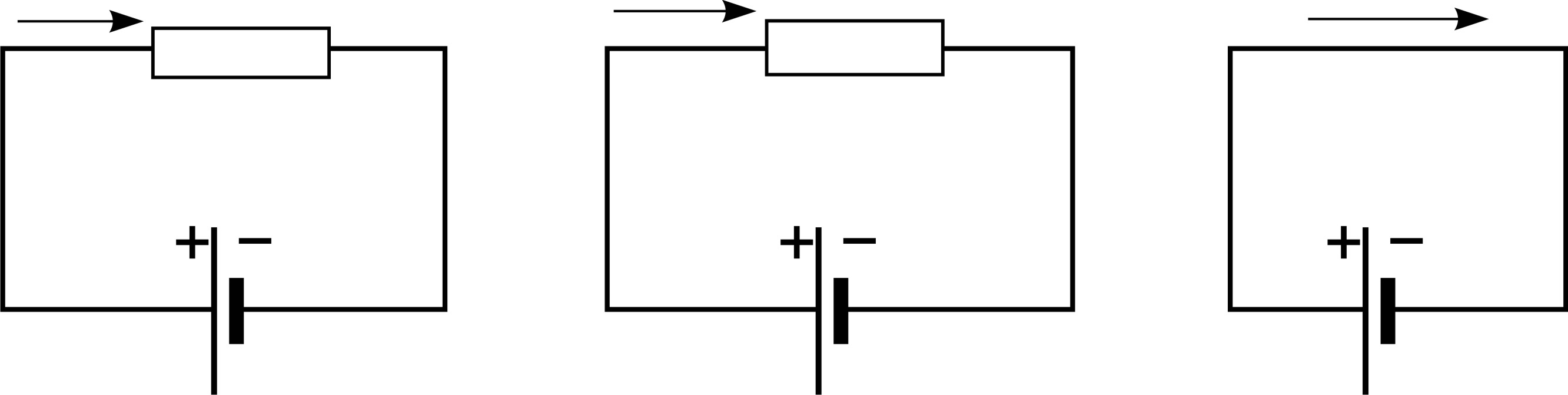
а б в
Рис. 44
1) Для замкнутых цепей (рис. 44 а и рис. 44 б) ток 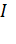 и ЭДС источника тока
и ЭДС источника тока  связаны законом Ома в следующем виде:
связаны законом Ома в следующем виде:
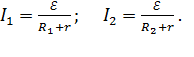 (1)
(1)
Из этих формул получаем следующие соотношения величин:
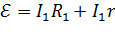 ;
;
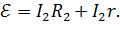
Приравнивая правые части записанных формул, исключаем неизвестную величину  и получаем расчетную формулу внутреннего сопротивления источника тока:
и получаем расчетную формулу внутреннего сопротивления источника тока:
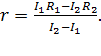 (2)
(2)
Чтобы найти сопротивления внешней цепи 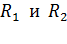 , используем закон Джоуля – Ленца – зависимость выделяемой мощности от величины сопротивления, в следующем виде:
, используем закон Джоуля – Ленца – зависимость выделяемой мощности от величины сопротивления, в следующем виде:
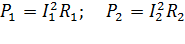 .
.
Из этих формул определяем сопротивления: 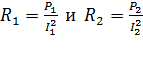 . Подставляя полученные значения сопротивлений в выражение (2), получаем расчетную формулу для величины
. Подставляя полученные значения сопротивлений в выражение (2), получаем расчетную формулу для величины  в следующем виде:
в следующем виде:
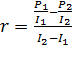 . (4)
. (4)
Вычисляем внутреннее сопротивление источника тока:
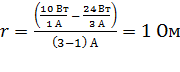 .
.
2) Электродвижущую силу источника тока  находим с помощью закона Ома (1):
находим с помощью закона Ома (1):
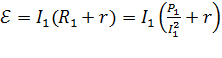 .
.
Вычисляем величину ЭДС: 
3) Ток короткого замыкания 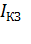 – это максимальный ток, который можно получить от данного источника тока. Он протекает в электрической цепи (рис. 44 в) при отсутствии внешнего сопротивления и, согласно закону Ома (1), определяется следующей формулой:
– это максимальный ток, который можно получить от данного источника тока. Он протекает в электрической цепи (рис. 44 в) при отсутствии внешнего сопротивления и, согласно закону Ома (1), определяется следующей формулой:
 ; вычисляем
; вычисляем 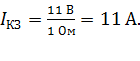
4) Коэффициент полезного действия 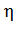 источника тока равен отношению полезной мощности, которая выделяется на внешнем сопротивлении (сопротивлении нагрузки), к полной мощности, которая выделяется во всей цепи, в том числе и в источнике тока. Используя закон Джоуля – Ленца, определяем величину КПД источника тока:
источника тока равен отношению полезной мощности, которая выделяется на внешнем сопротивлении (сопротивлении нагрузки), к полной мощности, которая выделяется во всей цепи, в том числе и в источнике тока. Используя закон Джоуля – Ленца, определяем величину КПД источника тока:
 .
.
Вычисляем значения КПД, используя формулы для сопротивлений нагрузки 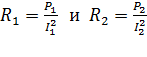 :
:
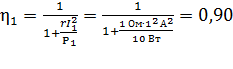 ;
;
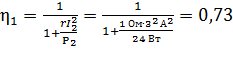 .
.
Задача 25. Электродвижущая сила источника тока 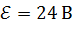 , ток короткого замыкания
, ток короткого замыкания 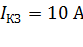 . Определите следующие величины: 1) сопротивление внешней цепи, при котором выделяется максимальная мощность
. Определите следующие величины: 1) сопротивление внешней цепи, при котором выделяется максимальная мощность 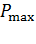 ; 2) величину
; 2) величину 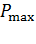 , которую можно получить от данного источника тока, и КПД
, которую можно получить от данного источника тока, и КПД 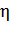 источника тока при этой мощности; 3) сопротивление нагрузки
источника тока при этой мощности; 3) сопротивление нагрузки 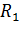 , при котором КПД
, при котором КПД  .
.
Дано Решение
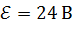 ;
; 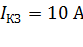 .
. 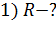 при
при 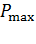
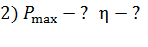 3)
3) 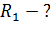 при
при 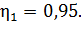
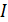
А

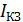
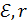
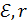
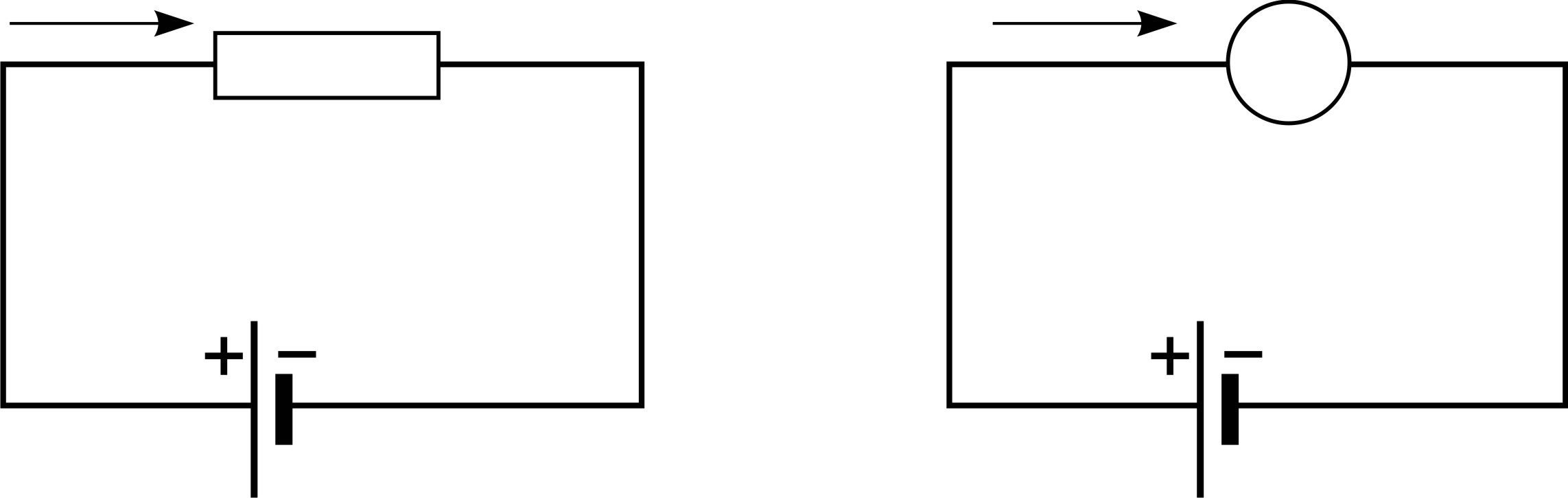
а б
Рис. 45
1) Мощность  , выделяемая в сопротивлении
, выделяемая в сопротивлении 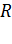 внешней цепи (рис. 45 а), определяется законом Джоуля – Ленца:
внешней цепи (рис. 45 а), определяется законом Джоуля – Ленца:
 (1)
(1)
где  – ток в цепи, который найдем по закону Ома для замкнутой цепи:
– ток в цепи, который найдем по закону Ома для замкнутой цепи:
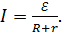 (2)
(2)
Здесь  – внутреннее сопротивление цепи, или сопротивление источника тока.
– внутреннее сопротивление цепи, или сопротивление источника тока.
2) Подставляя величину тока по формуле (2) в уравнение (1), получаем следующую формулу:
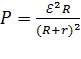 . (3)
. (3)
Зависимость полезной мощности, выделяемой в сопротивлении нагрузки 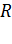 , от величины этого сопротивления, представленная формулой (3), имеет
, от величины этого сопротивления, представленная формулой (3), имеет 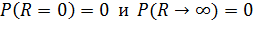 . Между этими нулевыми значениями есть максимальное
. Между этими нулевыми значениями есть максимальное 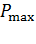 (так как величина
(так как величина 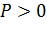 ). Запишем условие максимума функции
). Запишем условие максимума функции 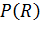 :
:
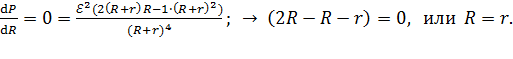 (4)
(4)
Таким образом, максимальная мощность развивается источником тока при сопротивлении нагрузки, равном сопротивлению источника тока.
Сопротивление источника тока  обычно измеряют методом вольтметра – амперметра в электрической цепи, схема которой приведена на рис. 45 б. Вольтметром измеряют ЭДС источника тока, в данной задаче она известна. Амперметром, сопротивление которого
обычно измеряют методом вольтметра – амперметра в электрической цепи, схема которой приведена на рис. 45 б. Вольтметром измеряют ЭДС источника тока, в данной задаче она известна. Амперметром, сопротивление которого 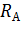 обычно мало (
обычно мало ( 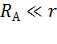 ), измеряют ток короткого замыкания
), измеряют ток короткого замыкания 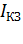 . Из формулы (2) закона Ома определяем сопротивление источника тока:
. Из формулы (2) закона Ома определяем сопротивление источника тока:
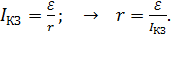 (5)
(5)
Тогда сопротивление нагрузки 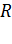 , при котором выделяется максимальная мощность
, при котором выделяется максимальная мощность
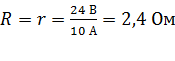 .
.
Для определения максимального значения мощности 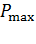 , которая выделяется на сопротивлении нагрузки
, которая выделяется на сопротивлении нагрузки 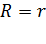 , подставим в уравнение (3) сопротивления
, подставим в уравнение (3) сопротивления 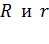 , найденные по формулам (4) и (5):
, найденные по формулам (4) и (5):
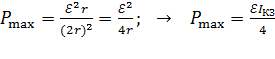 .
.
Вычисляем величину  .
.
Определим КПД источника тока как отношение мощностей:
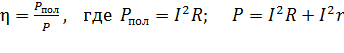 . (6)
. (6)
Здесь 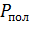 – полезная мощность, выделяемая на внешнем сопротивлении
– полезная мощность, выделяемая на внешнем сопротивлении 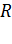 ;
;  – мощность источника тока, развиваемая во всей цепи. После подстановки величин этих мощностей в формулу для КПД получаем следующую расчетную формулу:
– мощность источника тока, развиваемая во всей цепи. После подстановки величин этих мощностей в формулу для КПД получаем следующую расчетную формулу:
 (7)
(7)
По этой формуле находим, что при выделении на нагрузке максимальной мощности 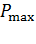 величина КПД
величина КПД
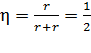 , или
, или 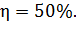
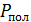
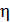
3) С помощью формулы (7) найдем внешнее сопротивление 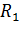 , соответствующее заданному значению КПД
, соответствующее заданному значению КПД 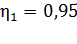 :
:

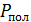
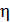
1,0
0,5
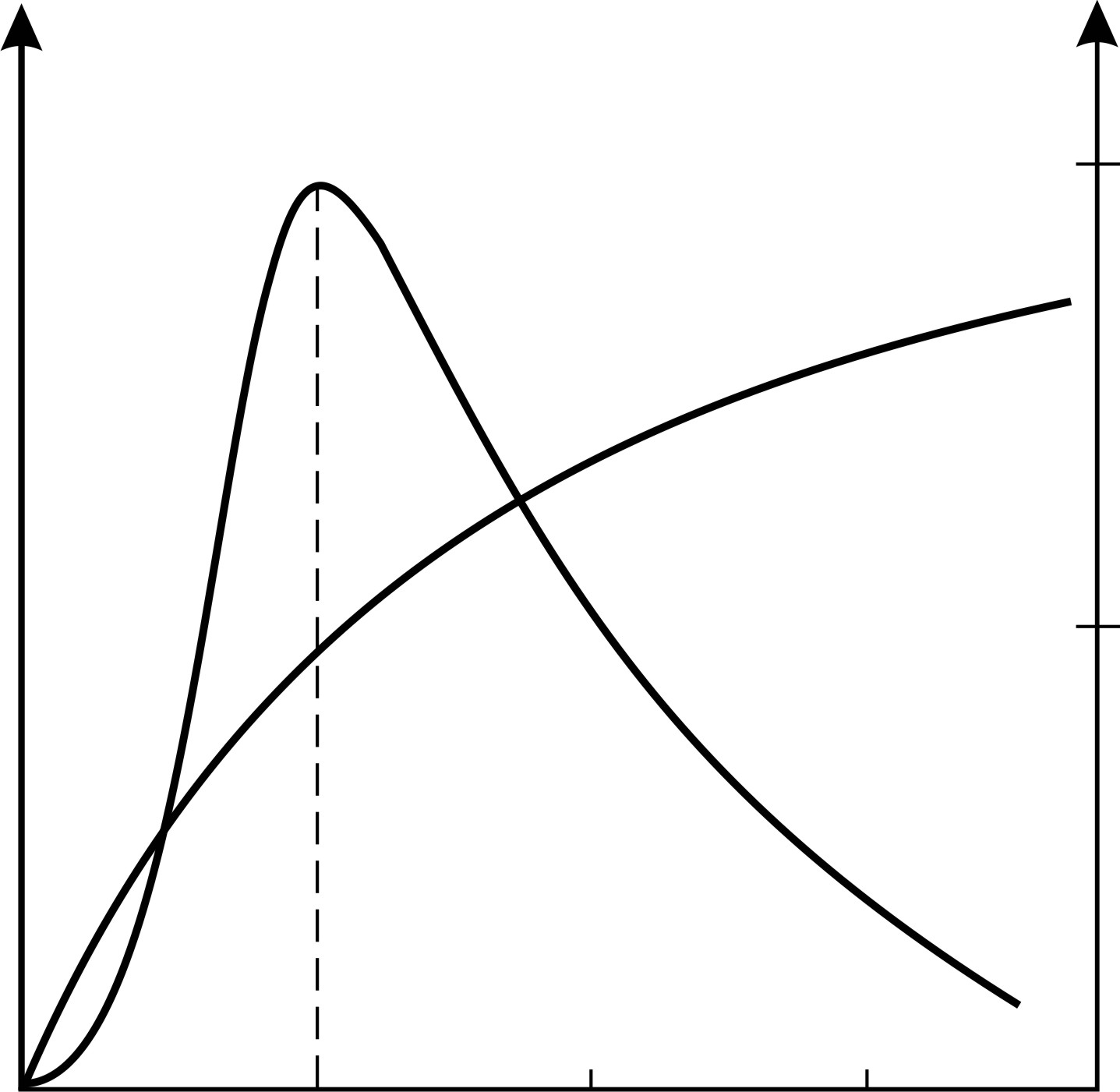
Рис. 46
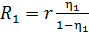 .
.
Вычисляем величину сопротивления нагрузки при КПД 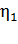 :
:
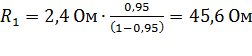 .
.
В заключение приведем примерные графики (рис. 46), которые показывают зависимости полезной мощности 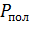 , выделяемой источником тока на внешнем сопротивлении
, выделяемой источником тока на внешнем сопротивлении 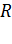 , и КПД
, и КПД 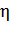 источника тока от отношения сопротивлений
источника тока от отношения сопротивлений 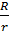 .
.
Задача 26. Нагреватель электрического чайника имеет две секции. При включении одной из них вода в чайнике закипает за время  , а при включении другой секции – через
, а при включении другой секции – через 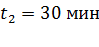 . Через какой промежуток времени
. Через какой промежуток времени  закипит вода в чайнике, если соединить обе секции: а) последовательно, б) параллельно?
закипит вода в чайнике, если соединить обе секции: а) последовательно, б) параллельно?
Дано Решение
 ;
; 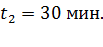 а) последовательно:
а) последовательно: 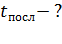 б) параллельно:
б) параллельно: 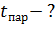
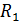
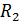
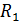
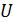
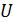
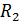
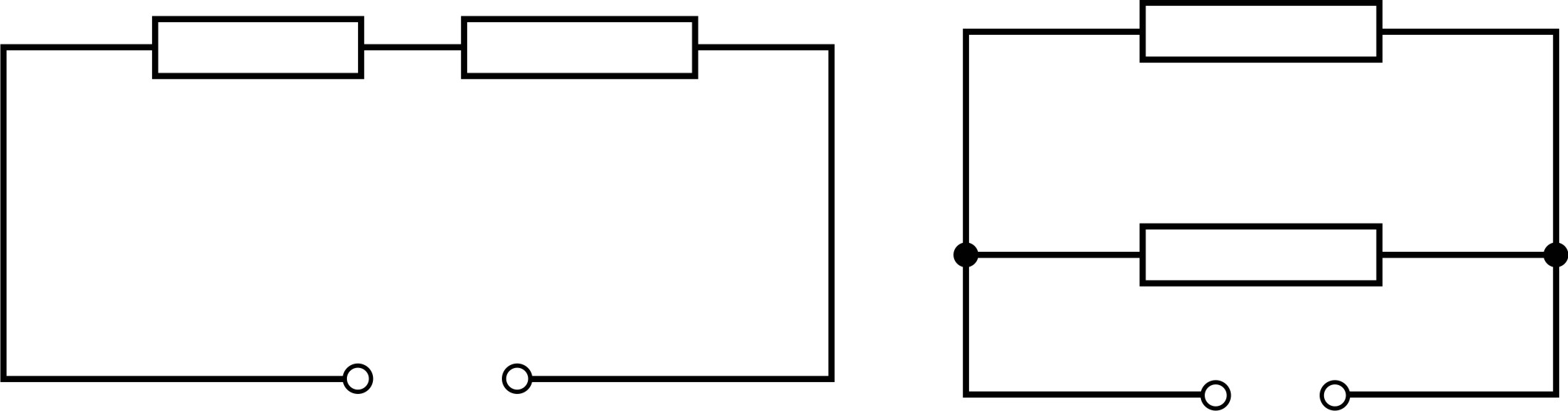
а б
Рис. 47
Для нагревания воды в чайнике до температуры кипения требуется определенное количество теплоты 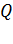 . Это необходимое количество теплоты выделяется на сопротивлении
. Это необходимое количество теплоты выделяется на сопротивлении 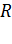 нагревателя при протекании в нем электрического тока
нагревателя при протекании в нем электрического тока  за время
за время  и, согласно закону Джоуля – Ленца, определяется следующей формулой:
и, согласно закону Джоуля – Ленца, определяется следующей формулой:
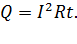 (1)
(1)
Так как токи через сопротивления 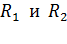 при последовательном (рис. 47 а) и параллельном (рис. 47 б) соединении этих сопротивлений различны, а одинаковая в этих двух случаях величина напряжения, на которое подключается нагреватель, то запишем ток по закону Ома:
при последовательном (рис. 47 а) и параллельном (рис. 47 б) соединении этих сопротивлений различны, а одинаковая в этих двух случаях величина напряжения, на которое подключается нагреватель, то запишем ток по закону Ома:
 (2)
(2)
Подставляя ток по формуле (2) в уравнение (1), получаем формулу для количества теплоты в следующем виде:
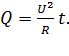 (3)
(3)
Выразим из уравнения (3) время  , необходимое для сообщения чайнику с водой требуемого количества теплоты:
, необходимое для сообщения чайнику с водой требуемого количества теплоты:
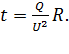 (4)
(4)
Из формулы (4) следует, что время нагрева  пропорционально сопротивлению нагревателя. Поэтому заданные в условии задачи величины
пропорционально сопротивлению нагревателя. Поэтому заданные в условии задачи величины 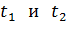 выразим через сопротивления каждой секции нагревателя, соответственно
выразим через сопротивления каждой секции нагревателя, соответственно 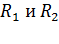 , согласно формуле (4):
, согласно формуле (4):
 . (5)
. (5)
Из последних соотношений выразим сопротивления секций, которые будут нужны для расчета сопротивления последовательного и параллельного соединения секций:
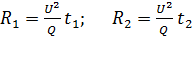 . (6)
. (6)
Представим искомые времена нагрева при двух соединениях сопротивлений 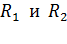 формулами, аналогичными соотношениям (5):
формулами, аналогичными соотношениям (5):
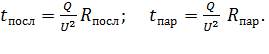 (7)
(7)
Здесь 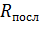 – сопротивление нагревателя при последовательном соединении секций сопротивлениями
– сопротивление нагревателя при последовательном соединении секций сопротивлениями 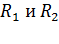 :
:
 ; (8)
; (8)
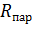 – сопротивление нагревателя при параллельном соединении сопротивлений
– сопротивление нагревателя при параллельном соединении сопротивлений 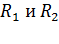 .
.
Так как
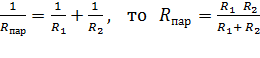 . ( 9)
. ( 9)
Подставляя значения сопротивлений нагревателя, представленные формулами (8) и (9), в соотношения (7), а затем, выражая величины 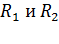 через заданные времена нагрева по формулам (6), получаем следующие расчетные формулы времени нагрева в двух случаях соединения секций нагревателя:
через заданные времена нагрева по формулам (6), получаем следующие расчетные формулы времени нагрева в двух случаях соединения секций нагревателя:
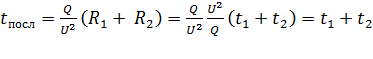 ; (10)
; (10)
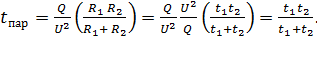 (11)
(11)
Вычисляем времена нагрева чайника при последовательном и параллельном соединениях секций по формулам (10) и (11):
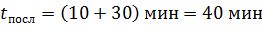 ;
;
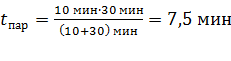 .
.
Таким образом, полученный результат показывает, что нагреватель, состоящий из двух секций с различными сопротивлениями, позволяет осуществлять нагрев с четырьмя различными скоростями.
Дата добавления: 2016-10-07; просмотров: 3384;











