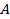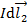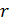Магнитное поле постоянного тока
Магнитная индукция 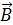 и напряженность
и напряженность 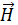 магнитного поля (МП) – его силовые характеристики. Связь величин
магнитного поля (МП) – его силовые характеристики. Связь величин 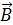 и
и 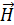 в однородной изотропной среде определяется соотношением
в однородной изотропной среде определяется соотношением
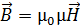 , (1)
, (1)
где 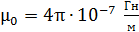 – магнитная постоянная,
– магнитная постоянная, 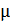 – магнитная проницаемость вещества: в вакууме
– магнитная проницаемость вещества: в вакууме 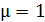 , для воздуха и других неферромагнитных сред
, для воздуха и других неферромагнитных сред 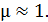 Равенство (1) показывает, что векторы
Равенство (1) показывает, что векторы 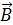 и
и 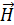 сонаправлены:
сонаправлены: 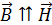 .
.
Закон Био – Савара – Лапласа: индукция магнитного поля 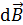 , создаваемого элементом тока
, создаваемого элементом тока 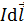 , определяется следующей формулой:
, определяется следующей формулой:
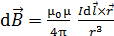 ; (2)
; (2)
модуль 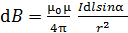 . (3)
. (3)
Здесь 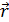 – радиус-вектор, проведенный от элемента тока до точки, в которой определяется магнитная индукция
– радиус-вектор, проведенный от элемента тока до точки, в которой определяется магнитная индукция 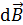 ;
; 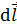 – вектор элемента длины проводника, направление которого совпадает с направлением тока, а модуль равен бесконечно малому отрезку
– вектор элемента длины проводника, направление которого совпадает с направлением тока, а модуль равен бесконечно малому отрезку 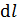 длины проводника;
длины проводника; 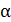 – угол между векторами
– угол между векторами 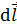 и
и 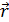 .
.
Согласно векторной форме закона (2), вектор магнитной индукции 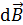 лежит в плоскости, перпендикулярной векторам
лежит в плоскости, перпендикулярной векторам 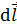 и
и 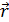 . Направление его определяется с помощью правила буравчика (правого винта) следующим образом (рис. 48).
. Направление его определяется с помощью правила буравчика (правого винта) следующим образом (рис. 48).
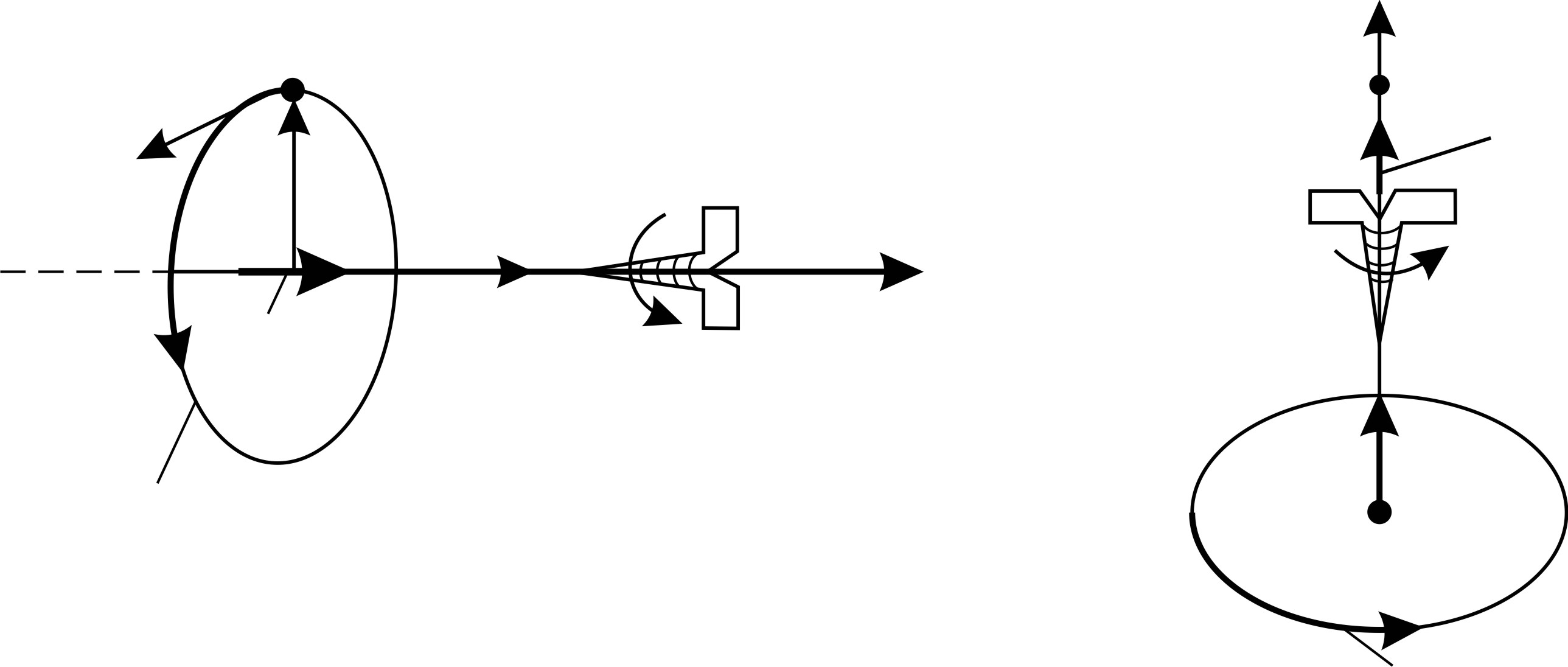
а Рис. 48 |
а) В случае прямого проводника с током (см. рис. 48 а) винт располагают вдоль тока 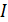 и вращают так, чтобы поступательное движение винта совпадало с током в проводнике. При этом вращательное движение головки винта показывает направление линий магнитного поля
и вращают так, чтобы поступательное движение винта совпадало с током в проводнике. При этом вращательное движение головки винта показывает направление линий магнитного поля 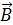 ; эти линии МП – окружности, лежащие в плоскости, перпендикулярной проводнику, и охватывающие его. Вектор
; эти линии МП – окружности, лежащие в плоскости, перпендикулярной проводнику, и охватывающие его. Вектор 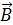 в каждой точке поля направлен по касательной к линии магнитной индукции.
в каждой точке поля направлен по касательной к линии магнитной индукции.
б) Если магнитное поле создается витком с током 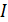 (см. рис. 48 б), то по направлению тока вращают винт, а поступательное движение винта показывает направление вектора
(см. рис. 48 б), то по направлению тока вращают винт, а поступательное движение винта показывает направление вектора 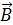 в любой точке на оси кругового тока.
в любой точке на оси кругового тока.
Магнитную индукцию поля, созданного проводником с током длины 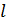 , рассчитывают с помощью принципа суперпозиции:
, рассчитывают с помощью принципа суперпозиции:
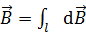 , (4)
, (4)
где векторы 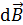 определяются законом Био – Савара – Лапласа (2), а суммирование векторов выполняют по всей длине проводника
определяются законом Био – Савара – Лапласа (2), а суммирование векторов выполняют по всей длине проводника 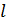 .
.
В случае, если МП создается несколькими токами 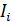 или проводником, состоящим из участков конечной длины
или проводником, состоящим из участков конечной длины 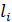 , имеющих различную форму, то магнитную индукцию
, имеющих различную форму, то магнитную индукцию 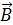 рассчитывают с помощью принципа суперпозиции в виде:
рассчитывают с помощью принципа суперпозиции в виде: 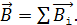 (5)
(5)
Здесь 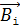 – вектор индукции МП, созданный i-тым участком проводника, величину которого определяют по формуле (4).
– вектор индукции МП, созданный i-тым участком проводника, величину которого определяют по формуле (4).
Подчеркнем, что в уравнениях (4) и (5) принципа суперпозиции выполняют суммирование векторов, учитывая их направление.
На основе принципа суперпозиции (4), посредством суммирования бесконечно малых векторов, получены следующие формулы для определения величины магнитной индукции:
1) в центре кругового проводника (витка радиусом  с током
с током 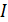 )
)
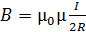 ; (6)
; (6)
2) бесконечно длинного прямого проводника с током в точке, находящейся на расстоянии 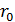 от проводника (по перпендикуляру)
от проводника (по перпендикуляру)
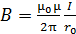 ; (7)
; (7)
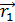
|
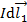
|
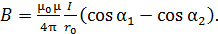 (8)
(8)
Здесь угол 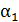 – между первым элементом тока
– между первым элементом тока 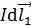 (отсчет ведется по направлению тока) и радиус-вектором
(отсчет ведется по направлению тока) и радиус-вектором 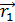 , проведенным от него в точку, где определяют магнитную индукцию
, проведенным от него в точку, где определяют магнитную индукцию 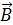 ;
; 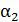 – угол между последним элементом тока
– угол между последним элементом тока 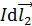 отрезка проводника и радиус-вектором
отрезка проводника и радиус-вектором 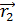 , задающим положение точки магнитного поля относительно этого элемента тока.
, задающим положение точки магнитного поля относительно этого элемента тока.
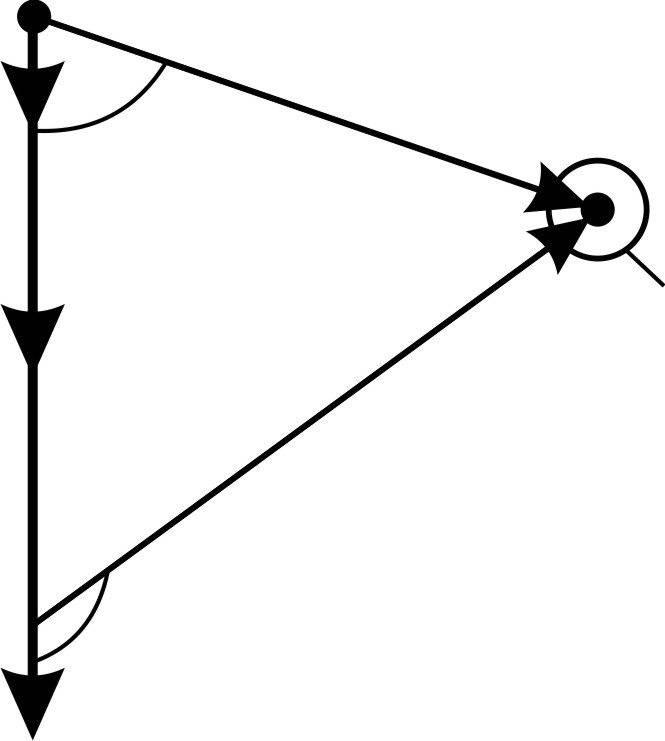
Рис. 49 |
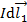
|
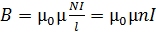 , (9)
, (9)
где 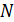 – число витков соленоида;
– число витков соленоида; 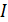 – ток в его обмотке;
– ток в его обмотке; 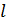 – длина сердечника, на котором располагаются витки,
– длина сердечника, на котором располагаются витки, 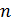 – число витков на единице длины обмотки соленоида.
– число витков на единице длины обмотки соленоида.
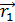
|
Магнитная индукция поля тороида (витки катушки намотаны на сердечник, имеющий форму тора (рис. 50 б)) внутри тора определяется также формулой (9), где 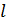 – длина осевой линии тора:
– длина осевой линии тора: 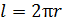 ; вне тора
; вне тора 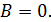
|
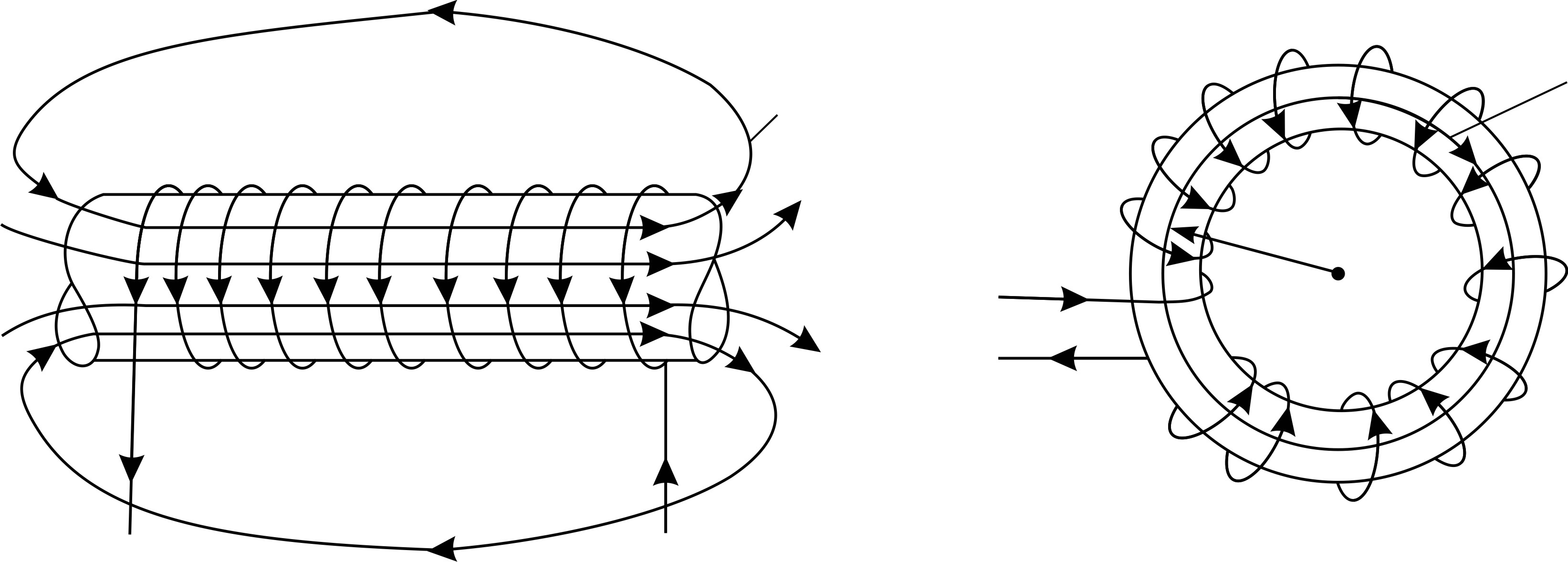
а б Рис. 50 |
Дата добавления: 2016-10-07; просмотров: 1963;