Интегрирование уравнений Эйлера

Для практического применения полученные уравнения Эйлера не всегда удобны, поэтому их следует проинтегрировать. Для этого запишем их в следующей форме:

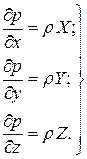(2.18)
Умножив каждое из уравнений (2.18) соответственно на dx, dy, dz и сложив их, получим

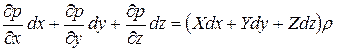.(2.19)

Так как р = f (x, y, z), то левая часть уравнения (2.19) есть полный дифференциал давления, то есть

dp = (Xdx + Ydy + Zdz)ρ. (2.20)

Уравнение (2.20) называется приведённым уравнением Эйлера.

При постоянном значении плотности ρ уравнение (2.20) имеет смысл лишь в том случае, когда правая его часть так же представляет собой полный дифференциал. А это возможно при условии существования функции u = f (x, y, z), частные производные которой по x, y, z будут равны:

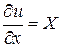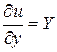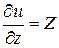; ; . (2.21)

Функция u называется силовой или потенциальной функцией, а силы, удовлетворяющие условиям (2.21), называют силами, имеющими потенциал (запас энергии).

Наиболее известные силы, имеющие потенциал – это силы тяжести и силы инерции.

Если проинтегрируем уравнение (2.20), то получим

р = ρu+C, (2.22)

где С – постоянная интегрирования.

Если для некоторой точки, находящейся на поверхности или внутри жидкости известны давление р₀ и потенциальная функция u₀, то

C = р₀ – ρu₀ , тогда

р = р₀ + ρ(u – u₀). (2.23)

Выражение (2.23) является интегралом приведённого уравнения Эйлера. С его помощью можно определить гидростатическое давление в различных точках при известных значениях потенциальной функции. Наибольшее практическое значение имеют случаи применения выражения (2.23) для абсолютного и относительного покоя жидкости в условиях земного тяготения. Именно эти задачи будут рассматриваться далее.