Гидродинамическое подобие (подобные преобразования уравнений Навье-Стокса) и вывод основных критериев ГД подобия.

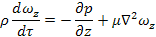
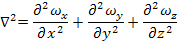
Преобразуем уравнение Навье-Стокса для оси OZ в соответствии с положениями теории подобия.

· Установившийся поток.

Последовательность преобразования:

1. Отбрасываем знаки дифференциала;

2. Считаем геометрический размер z=l (линейным)

Для установившегося режима отсутствуют изменения технологической переменной во времени, поэтому в левой части уравнения заменяем отношение дифференциалов на отношение конечных величин.

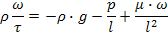
3. Делим все слагаемые на ρ

4. Учитывая, что время может быть выражено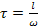

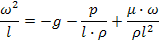
5. Делим правую часть на левую

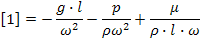
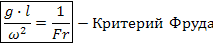
Отражает влияние силы тяжести на движение жидкости и характеризует отношение сил инерции к силе тяжести в подобных потоках.

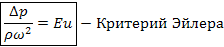
Это отношение сил давления к силе инерции. Отражает влияние перепада гидростатического давления на давление жидкости.

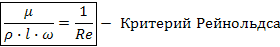
Отражает влияние силы трения на движение жидкости.

· Неустановившийся режим.

Помимо этих критериев имеет место:

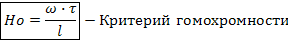
Критерии Рейнольдса, Фруда и гомохромности составлены из величин определяющих распределение скоростей в потоке, и поэтому являются определяющими критериями ГД подобия.

Критерий Эйлера включает в себя абсолютное давление, которое нужно определить, т.к. если знать разность – известна движущая сила, поэтому он является определяемым критерием.

Т.о., чтобы процессы, происходящие в модели и в натуре, были подобны в сходных точках, должно осуществляться равенство:

Re'=Re'', Fr'=Fr'', Ho'=Ho'', Eu'=Eu''

Согласно второй теории подобия, критерии подобия должны быть связаны между собой критериальным уравнением:

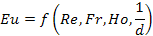
Необходимо учитывать симплекс геометрического подобия.

Любую функциональную зависимость можно описать степенной функцией

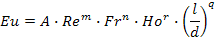
Путем обработки опытных данных на моделях находят численные значения коэффициента А и степеней m,n,r,q и получают обобщенное критериальное уравнение ГД для данного процесса.

Если процесс установившийся:

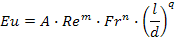
При турбулентном движении капельных жидкостей и газов, перемещаемых с помощью насосов и компрессоров, влияние силы тяжести на распределение скоростей и перепад давления незначительно, поэтому Fr может быть исключен:

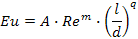
Некоторые физические величины, входящие в критерии подобия, целесообразно заменять на другие им пропорциональные, т.к. иногда бывает почти невозможно экспериментально определить ту или иную физическую величину, входящую в критерий подобия; поэтому используются производные от остальных критериев подобия.

Т.о. получают критерий подобия для естественной конвекции, т.е. движении, возникающем вследствие разности плотностей

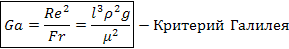
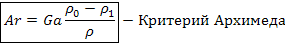
Критериальное уравнение подобия процесса можно получить, используя метод анализа размерностей.

Один из методов обработки экспериментальных данных с получением критериального уравнения – π – теорема Бекингема, согласно которой общая функциональная зависимость, связывающая между собой n переменных величин при m основных единицах измерения может быть представлена в виде зависимости между (n-m) безразмерных комплексов этих величин, а при наличии подобия в виде связи между этим количеством критериев подобия.