Глава 3. Матрицы и системы уравнений
Первоначально матрицы были введены для упрощения записи систем линейных уравнений. Система линейных уравнений:
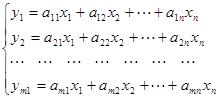
записывается одним матричным равенством 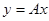 , где
, где 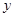 столбцевая матрица
столбцевая матрица 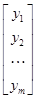 ,
, 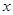 столбцевая матрица
столбцевая матрица 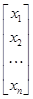 , а
, а  –
– 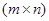 -матрица
-матрица 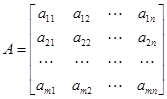 .
.
На языке матриц линейное преобразование 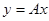 означает преобразование столбца
означает преобразование столбца 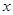 в столбец
в столбец 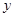 , которое определяется матрицей преобразования
, которое определяется матрицей преобразования  .
.
Пусть задана система 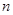 линейных уравнений с
линейных уравнений с 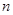 неизвестными
неизвестными
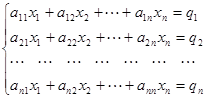
В матричной форме эта система уравнений запишется как 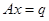 , где
, где  – квадратная матрица
– квадратная матрица 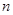 -го порядка, называемая матрицей системы;
-го порядка, называемая матрицей системы; 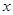 и
и 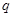 – столбцевые матрицы неизвестных переменных и свободных членов.
– столбцевые матрицы неизвестных переменных и свободных членов.
Матричное уравнение 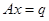 решается умножением обеих его частей слева на обратную матрицу
решается умножением обеих его частей слева на обратную матрицу 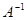 , т. е.
, т. е. 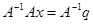 , в результате чего получаем
, в результате чего получаем 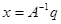 . В соответствии с правилом Крамера неизвестные
. В соответствии с правилом Крамера неизвестные 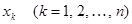 определяются соотношением:
определяются соотношением:
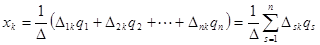 ,
,
где 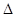 – определитель системы уравнений и
– определитель системы уравнений и 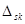 – алгебраические дополнения. Определитель
– алгебраические дополнения. Определитель 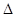 представляет собой числовую функцию, которая вычисляется по определенным правилам на основании квадратной таблицы, состоящей из коэффициентов системы уравнений
представляет собой числовую функцию, которая вычисляется по определенным правилам на основании квадратной таблицы, состоящей из коэффициентов системы уравнений
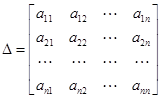 .
.
Табличное представление определителя 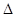 по форме совпадает с матрицей системы уравнений, т. е. состоит из тех же элементов и в том же порядке, что и матрица
по форме совпадает с матрицей системы уравнений, т. е. состоит из тех же элементов и в том же порядке, что и матрица  . В таких случаях его называют определителям матрицы
. В таких случаях его называют определителям матрицы  и записывают
и записывают 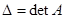 .
.
Общее выражение для определителя матрицы 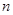 -го порядка записывается в виде:
-го порядка записывается в виде:
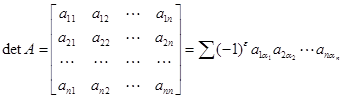 .
.
В правой части стоит сумма произведении вида 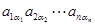 . Каждое такое произведение по определению должно содержать элементы матрицы
. Каждое такое произведение по определению должно содержать элементы матрицы 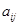 , расположенные в различных строках и различных столбцах. Это значит, что среди всех первых индексов, как и среди всех вторых индексов не должно быть одинаковых. Если расположить первые индексы в порядке их возрастания, как это сделано выше, то совокупность вторых индексов образует некоторую перестановку (
, расположенные в различных строках и различных столбцах. Это значит, что среди всех первых индексов, как и среди всех вторых индексов не должно быть одинаковых. Если расположить первые индексы в порядке их возрастания, как это сделано выше, то совокупность вторых индексов образует некоторую перестановку ( 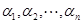 ) множества чисел от 1 до
) множества чисел от 1 до 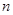 . Определитель равен сумме всех таких произведений, взятых со знаком
. Определитель равен сумме всех таких произведений, взятых со знаком 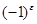 , где
, где 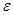 – число инверсий перестановки (
– число инверсий перестановки ( 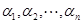 ). Как известно, инверсию образуют два числа в перестановке, когда меньшее из них расположено правее большего.
). Как известно, инверсию образуют два числа в перестановке, когда меньшее из них расположено правее большего.
Для вычисления определителей второго и третьего порядка можно записать выражения
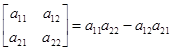
и
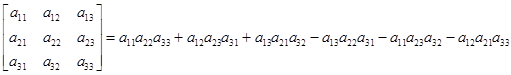 ,
,
которые совпадают со схемами вычисления этих определителей (рис. 3):
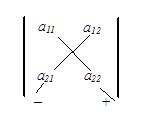
| 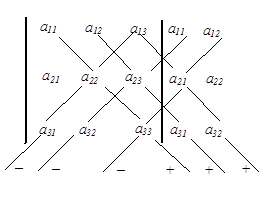
|
| Рис. 3 |
Как видно, индексы столбцов всех членов определителя третьего порядка определяются перестановками (1, 2, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1), (1, 3, 2), (2, 1, 3), число инверсий которых равно соответственно 0, 2, 2, 3, 1, 1.
Перечисляя основные свойства определителей, прежде всего отметим, что 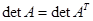 , т. е. определитель матрицы не изменяет своего значения при взаимной замене ее строк и столбцов. Поэтому все свойства определителя, сформулированные ниже для столбцов, справедливы и для строк, и обратно.
, т. е. определитель матрицы не изменяет своего значения при взаимной замене ее строк и столбцов. Поэтому все свойства определителя, сформулированные ниже для столбцов, справедливы и для строк, и обратно.
1. При перестановке двух столбцов определитель меняет знак (свойство антисимметрии).
2. Определитель равен нулю, если все элементы какого-нибудь столбца равны нулю или если один из столбцов является линейной комбинацией любых его других столбцов (в частности, определитель, у которого хотя бы два столбца одинаковы, равен нулю).
3. Умножение всех элементов какого-нибудь столбца на скаляр 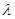 равнозначно умножению определителя на
равнозначно умножению определителя на 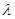 (общий множитель элементов строки или столбца можно вынести за знак определителя).
(общий множитель элементов строки или столбца можно вынести за знак определителя).
4. Умножение матрицы 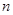 -го порядка на скаляр
-го порядка на скаляр 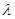 соответствует умножению ее определителя на
соответствует умножению ее определителя на 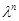 , т. е.
, т. е. 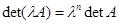 .
.
5. Значение определителя не изменится, если к какому-нибудь столбцу прибавить другой столбец, умноженный на скаляр 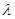 .
.
6. Если два определителя одинаковых порядков различаются между собой только элементами 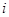 -го столбца, то их сумма равна определителю, элементы
-го столбца, то их сумма равна определителю, элементы 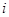 -го столбца которого равны суммам соответствующих элементов
-го столбца которого равны суммам соответствующих элементов 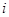 -х столбцов исходных определителей, а остальные элементы те же, что у исходных (свойство линейности).
-х столбцов исходных определителей, а остальные элементы те же, что у исходных (свойство линейности).
Алгебраическое дополнение 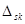 вычисляется как определитель матрицы, полученной удалением из матрицы
вычисляется как определитель матрицы, полученной удалением из матрицы 
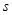 -й строки и
-й строки и 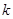 -го столбца, причем этот определитель умножается еще на
-го столбца, причем этот определитель умножается еще на 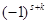 . Величину
. Величину 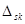 называют также алгебраическим дополнением элемента
называют также алгебраическим дополнением элемента 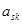 матрицы
матрицы  .
.
Используя введенные понятия определителя и алгебраического дополнения можно установить способ получения обратной матрицы, который не был определен ранее. Записав для всех элементов столбцевой матрицы 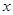 выражения по правилам Крамера, получим решение системы уравнений в виде:
выражения по правилам Крамера, получим решение системы уравнений в виде:
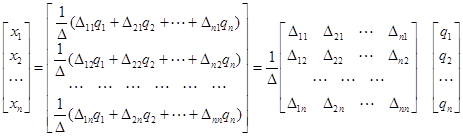 ,
,
откуда, сравнивая с 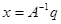 , можно записать
, можно записать
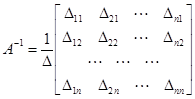 .
.
Из полученного выражения следует правило определения обратной матрицы: 1) элементы 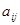 , данной матрицы
, данной матрицы 
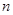 -го порядка заменяются их алгебраическими дополнениями
-го порядка заменяются их алгебраическими дополнениями 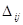 ;2) матрица алгебраических дополнений транспонируется, в результате чего получаем присоединенную матрицу к
;2) матрица алгебраических дополнений транспонируется, в результате чего получаем присоединенную матрицу к  (она обозначается через
(она обозначается через 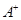 ); 3) вычисляется определитель
); 3) вычисляется определитель 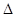 матрицы
матрицы  и присоединенная матрица
и присоединенная матрица 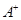 умножается на величину, обратную этому определителю.
умножается на величину, обратную этому определителю.
Вычисление таким методом обратной матрицы иллюстрируется приведенным ниже примером:
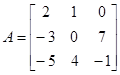
| 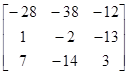
| 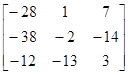
| 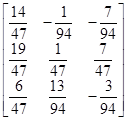
|
исходная матрица  ; ; 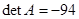
| 1) матрица алгебраических дополнений | 2) присоединенная матрица 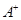
| 3) обратная матрица 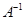
|
Однако такой путь является слишком громоздким, так как он требует вычисления определителя 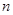 -го порядка и
-го порядка и 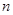 определителей
определителей 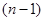 -го порядка. Для решения этой задачи разработано много более практичных алгоритмов, один из которых основан методе исключения.
-го порядка. Для решения этой задачи разработано много более практичных алгоритмов, один из которых основан методе исключения.
Метод исключения основан на том, уравнение 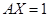 можно решить относительно
можно решить относительно 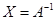 преобразованием матрицы
преобразованием матрицы  к единичной при условии соблюдения равенства его левой и правой частей. Воспользуемся для этого следующей процедурой. Разделим элементы первой строки матрицы
к единичной при условии соблюдения равенства его левой и правой частей. Воспользуемся для этого следующей процедурой. Разделим элементы первой строки матрицы  на
на 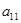 и прибавим к остальным строкам эту строку, умноженную на
и прибавим к остальным строкам эту строку, умноженную на 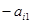 (
( 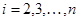 ). В результате получим
). В результате получим 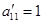 , а остальные элементы первого столбца обратятся в нуль. Далее вторую строку делим на новое значение
, а остальные элементы первого столбца обратятся в нуль. Далее вторую строку делим на новое значение 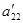 и прибавляем к остальным строкам эту строку, умноженную на новые значения
и прибавляем к остальным строкам эту строку, умноженную на новые значения 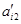 (
( 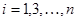 ). В результате получим
). В результате получим 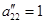 , а остальные элементы второго столбца равны нулю. Через
, а остальные элементы второго столбца равны нулю. Через 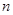 таких шагов матрица
таких шагов матрица  преобразуется в единичную матрицу. На
преобразуется в единичную матрицу. На 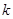 -м шаге строки матрицы
-м шаге строки матрицы 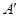 , полученной на предыдущем шаге, преобразуются следующим образом:
, полученной на предыдущем шаге, преобразуются следующим образом: 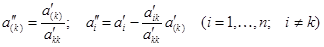 , что можно представить как умножение
, что можно представить как умножение 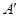 слева на некоторую матрицу
слева на некоторую матрицу 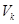 того же порядка, т. е.
того же порядка, т. е. 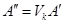 . Так как
. Так как 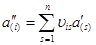 , то сравнивая с приведенными выше соотношениями, находим
, то сравнивая с приведенными выше соотношениями, находим 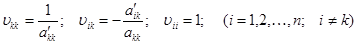 , а остальные элементы матрицы
, а остальные элементы матрицы 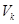 равны нулю.
равны нулю.
Очевидно, произведение 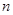 таких матриц для
таких матриц для 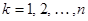
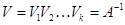 и осуществляет преобразование
и осуществляет преобразование  к единичной матрице. Чтобы равенство
к единичной матрице. Чтобы равенство 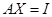 не нарушилось при умножении
не нарушилось при умножении  на
на 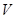 слева, необходимо правую часть также умножить на
слева, необходимо правую часть также умножить на 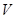 , т. е.
, т. е. 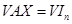 . А это значит, что над строками единичной матрицы в правой части уравнения в процессе его преобразования необходимо выполнить те же операции, что и над строками матрицы
. А это значит, что над строками единичной матрицы в правой части уравнения в процессе его преобразования необходимо выполнить те же операции, что и над строками матрицы  . Это удобно реализовать, оперируя над строками расширенной матрицы
. Это удобно реализовать, оперируя над строками расширенной матрицы 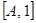 и выбирая в качестве опорных элементов диагональные элементы матрицы
и выбирая в качестве опорных элементов диагональные элементы матрицы  . Проиллюстрируем метод исключения на примере обращения матрицы
. Проиллюстрируем метод исключения на примере обращения матрицы 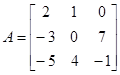 :
:
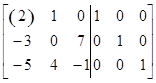
| 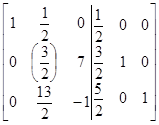
|
| Шаг 1 | Шаг 2 |
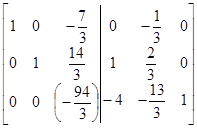
| 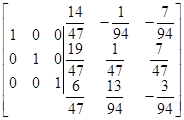
|
| Шаг 3 | Шаг 4 |
В итоге получаем обратную матрицу, расположенную в трех последних столбцах. Как побочный результат, имеем также определитель матрицы  , равный произведению тех значений опорных элементов, которые они принимают на соответствующих шагах преобразования матрицы
, равный произведению тех значений опорных элементов, которые они принимают на соответствующих шагах преобразования матрицы 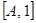 (эти элементы выделены круглыми скобками):
(эти элементы выделены круглыми скобками): 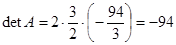 . Кроме того, одновременно вычисляется и присоединенная матрица
. Кроме того, одновременно вычисляется и присоединенная матрица
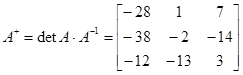 .
.
Обратная матрица существует для матрицы  при условии, что
при условии, что 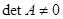 . Такие матрицы называются неособенными, в отличие от особенных (вырожденных), определитель которых равен нулю. Подытожим изложенные ранее свойства обратных матриц и приведем некоторые другие их свойства.
. Такие матрицы называются неособенными, в отличие от особенных (вырожденных), определитель которых равен нулю. Подытожим изложенные ранее свойства обратных матриц и приведем некоторые другие их свойства.
1. Если существуют 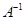 и
и 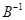 , то существует и
, то существует и 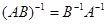 .
.
2. 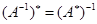 .
.
3. 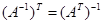 .
.
4. 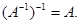
5. 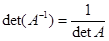 .
.
6. Если 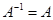 , матрица
, матрица  называется инволютивной (взаимно обратной).
называется инволютивной (взаимно обратной).
В общем случае число уравнений 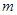 может отличаться от числа неизвестных. Такая система
может отличаться от числа неизвестных. Такая система
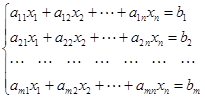
в матричной форме 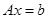 характеризуется прямоугольной матрицей коэффициентов
характеризуется прямоугольной матрицей коэффициентов  размера
размера 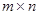 и столбцом свободных членов
и столбцом свободных членов 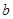 . Если все свободные члены равны нулю, то система называется однородной, а если среди них имеется хотя бы один ненулевой член, то система называется неоднородной.
. Если все свободные члены равны нулю, то система называется однородной, а если среди них имеется хотя бы один ненулевой член, то система называется неоднородной.
Среди уравнений системы могут быть линейно-зависимые, т. е. такие, которые можно представить как результат сложения других уравнений, умноженных на какие-либо числа (при умножении уравнения на число его левая и правая части умножаются на это число). Ясно, что зависимые уравнения не содержат никакой дополнительной информации, влияющей на значения искомых величин. Исключение зависимых уравнений приводит к эквивалентной системе, решение которой совпадает с решением исходной системы. Число независимых уравнений определяет ранг системы. Соответственно число независимых строк (или столбцов) матрицы называют рангом матрицы.
Система 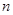 уравнений с
уравнений с 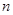 неизвестными
неизвестными 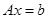 , матрица которой
, матрица которой  является неособенной, т. е.
является неособенной, т. е. 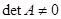 , имеет единственное решение
, имеет единственное решение 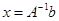 и называется определенной системой
и называется определенной системой 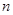 -го порядка. Ранг неособенной матрицы
-го порядка. Ранг неособенной матрицы  равен ее порядку (
равен ее порядку ( 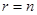 ). Если среди
). Если среди 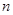 уравнений имеются зависимые, то
уравнений имеются зависимые, то  – особенная матрица и ее ранг меньше порядка (
– особенная матрица и ее ранг меньше порядка ( 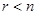 ). Разность
). Разность 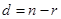 называют дефектом матрицы, а саму матрицу –
называют дефектом матрицы, а саму матрицу – 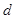 -кратно вырожденной. После исключения
-кратно вырожденной. После исключения 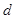 зависимых уравнений получим эквивалентную систему
зависимых уравнений получим эквивалентную систему 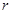 уравнений с
уравнений с 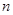 неизвестными.
неизвестными.
Система 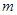 уравнений с
уравнений с 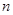 неизвестными при
неизвестными при 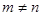 может иметь решение, а может и не иметь их вовсе. Если система имеет хотя бы одно решение, ее называют совместной, а систему, для которой решение не существует, называют несовместной. Необходимым и достаточным условием совместности системы линейных уравнений согласно теореме Кронекера – Капелли является равенство рангов матрицы
может иметь решение, а может и не иметь их вовсе. Если система имеет хотя бы одно решение, ее называют совместной, а систему, для которой решение не существует, называют несовместной. Необходимым и достаточным условием совместности системы линейных уравнений согласно теореме Кронекера – Капелли является равенство рангов матрицы  и ее расширенной матрицы
и ее расширенной матрицы 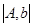 , где
, где 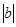 – столбец свободных членов. Совместная система при
– столбец свободных членов. Совместная система при 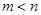 всегда имеет бесконечное множество решений и называется неопределенной. При
всегда имеет бесконечное множество решений и называется неопределенной. При 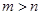 система является либо несовместной, либо сводится к эквивалентной ей совместной системе, которая может быть определенной (
система является либо несовместной, либо сводится к эквивалентной ей совместной системе, которая может быть определенной ( 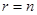 ) или неопределенной (
) или неопределенной ( 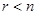 ).
).
Для решения неоднородных систем линейных уравнений 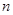 -го порядка идея исключения нашла применение в алгоритме Гаусса. Он сводится к последовательному исключению неизвестных, в результате чего данная система уравнений преобразуется к эквивалентной системе с верхней треугольной матрицей, решение которой не составляет труда. Подобно методу исключения при обращении матрицы, это достигается соответствующими операциями над строками расширенной матрицы системы
-го порядка идея исключения нашла применение в алгоритме Гаусса. Он сводится к последовательному исключению неизвестных, в результате чего данная система уравнений преобразуется к эквивалентной системе с верхней треугольной матрицей, решение которой не составляет труда. Подобно методу исключения при обращении матрицы, это достигается соответствующими операциями над строками расширенной матрицы системы 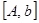 размера
размера 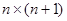 . Различие заключается в том, что в нули преобразуются лишь те элементы матрицы
. Различие заключается в том, что в нули преобразуются лишь те элементы матрицы  , которые расположены ниже ее главной диагонали. В результате
, которые расположены ниже ее главной диагонали. В результате 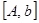 приводится к матрице
приводится к матрице 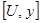 , где
, где 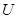 – верхняя треугольная матрица с единичными элементами на главной диагонали;
– верхняя треугольная матрица с единичными элементами на главной диагонали; 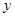 – преобразованный столбец свободных членов:
– преобразованный столбец свободных членов:
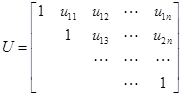 ;
; 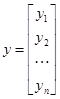 .
.
Преобразованная система имеет вид:
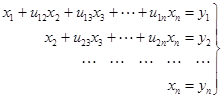 ,
,
откуда на основании 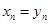 находятся последовательно
находятся последовательно 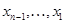 по формуле:
по формуле:
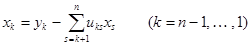 .
.
Итак, алгоритм Гаусса содержит два этапа: 1) построение вспомогательной системы с треугольной матрицей 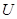 (прямой ход); 2) получение решения системы
(прямой ход); 2) получение решения системы 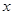 (обратный ход). Проиллюстрируем его на следующем примере. Пусть задана система уравнений:
(обратный ход). Проиллюстрируем его на следующем примере. Пусть задана система уравнений: 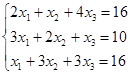 . Расширенная матрица
. Расширенная матрица 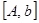 для этой системы имеет вид:
для этой системы имеет вид: 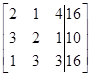 . Прямой ход включает в себя следующие преобразования расширенной матрицы:
. Прямой ход включает в себя следующие преобразования расширенной матрицы:

| 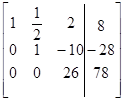
| 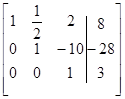
|
| Шаг 1 | Шаг 2 | Шаг 3 |
Преобразованная система уравнений имеет вид:
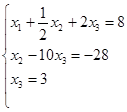 ,
,
откуда находим: 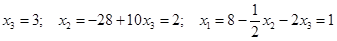 .
.
Если исключение выполнить так же, как при обращении матрицы, которое рассмотрено ранее, то в результате матрица 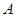 преобразуется в единичную, а
преобразуется в единичную, а 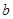 – в столбец, элементы которого равны значениям искомых величин
– в столбец, элементы которого равны значениям искомых величин 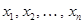 , т. е.
, т. е. 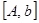 преобразуется в
преобразуется в 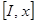 . Эту разновидность метода исключения называют алгоритмом Гаусса – Жордана. Так, для рассматриваемого примера имеем
. Эту разновидность метода исключения называют алгоритмом Гаусса – Жордана. Так, для рассматриваемого примера имеем
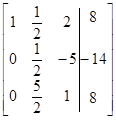
| 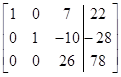
| 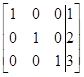
|
| Шаг 1 | Шаг 2 | Шаг 3 |
откуда сразу получаем 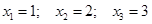 .
.
Многие задачи механики, электротехники, радиоэлектроники и других отраслей техники связаны с решением системы линейных уравнений, правые части которых принимают различные значения, а матрица системы остается неизменной. Совокупность таких систем 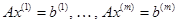 можно рассматривать как одно матричное уравнение
можно рассматривать как одно матричное уравнение 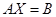 , где
, где  и
и  – матрицы размера
– матрицы размера 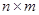 , столбцы которых равны соответственно
, столбцы которых равны соответственно 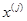 и
и 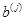
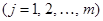 . Как уже указывалось ранее, решение уравнения
. Как уже указывалось ранее, решение уравнения 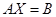 можно представить через обратную матрицу
можно представить через обратную матрицу 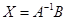 . Часто, однако, отдают предпочтение процедурам исключения, которые выполняются над расширенной матрицей
. Часто, однако, отдают предпочтение процедурам исключения, которые выполняются над расширенной матрицей 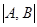 . Пусть, например, требуется решить уравнение
. Пусть, например, требуется решить уравнение 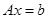 при заданной матрице
при заданной матрице 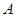 и различных векторах в правой части, т. е.
и различных векторах в правой части, т. е.
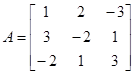 ;
; 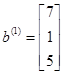 ;
; 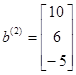 .
.
Запишем расширенную матрицу 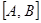
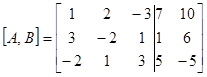
и преобразуем ее в соответствии с алгоритмом Гаусса – Жордана:
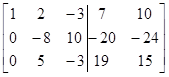
| 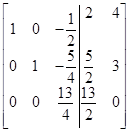
| 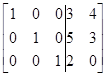
|
| Шаг 1 | Шаг 2 | Шаг 3 |
Отсюда имеем:
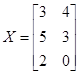 ;
; 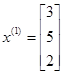 ;
; 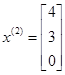 .
.
В общем случае, когда число уравнений 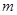 не равно числу неизвестных
не равно числу неизвестных 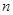 , также применима процедура исключения, причем в процессе ее реализации выявляется и характер системы. Пусть, например, дана система уравнений:
, также применима процедура исключения, причем в процессе ее реализации выявляется и характер системы. Пусть, например, дана система уравнений:
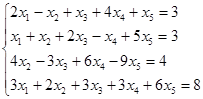 .
.
Запишем расширенную матрицу 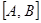
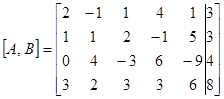
и преобразуем ее в соответствии с алгоритмом Гаусса – Жордана:
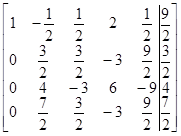
| 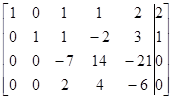
| 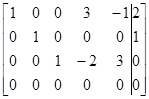
|
| Шаг 1 | Шаг 2 | Шаг 3 |
Последняя нулевая строка соответствует тождеству 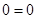 , что свидетельствует о зависимости исходных уравнений. Так как независимых уравнений три, то и ранг системы
, что свидетельствует о зависимости исходных уравнений. Так как независимых уравнений три, то и ранг системы 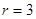 . Таким образом, получаем эквивалентную систему уравнений:
. Таким образом, получаем эквивалентную систему уравнений: 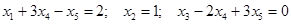 , решение которой:
, решение которой: 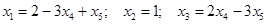 , где
, где 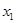 и
и 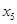 могут принимать произвольные значения. Рассмотренная система является совместной и неопределенной, так как имеет бесконечное множество решений.
могут принимать произвольные значения. Рассмотренная система является совместной и неопределенной, так как имеет бесконечное множество решений.
При любом числе 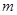 уравнений ранг системы не может превышать число неизвестных
уравнений ранг системы не может превышать число неизвестных 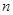 (
( 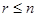 ). Если
). Если 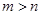 , то не менее (
, то не менее ( 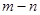 ) уравнений совместной системы зависимы и превращаются в тождества в процессе исключения. Совместная система
) уравнений совместной системы зависимы и превращаются в тождества в процессе исключения. Совместная система 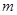 уравнений ранга
уравнений ранга 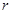 имеет
имеет 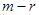 зависимых уравнений. При
зависимых уравнений. При 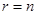 она определенная, а при
она определенная, а при 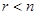 неопределенная.
неопределенная.
Система, все свободные члены которой равны нулю ( 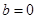 ), называется однородной. Она всегда совместна, гак как нулевой столбец
), называется однородной. Она всегда совместна, гак как нулевой столбец 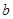 не влияет на ранг расширенной матрицы
не влияет на ранг расширенной матрицы 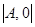 . Однородная система
. Однородная система 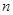 уравнений с
уравнений с 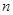 неизвестными имеет тривиальное решение
неизвестными имеет тривиальное решение 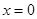 , которое и единственно, если ранг матрицы
, которое и единственно, если ранг матрицы 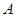 равен ее порядку (
равен ее порядку ( 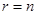 ). При
). При 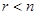 однородная система имеет бесконечное множество решений и сводится к неопределенной системе
однородная система имеет бесконечное множество решений и сводится к неопределенной системе 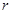 уравнений с
уравнений с 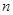 неизвестными. Это, в частности, означает, что система
неизвестными. Это, в частности, означает, что система 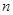 уравнений с
уравнений с 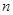 неизвестными имеет нетривиальные решения при условии, что матрица системы особенна, т. е.
неизвестными имеет нетривиальные решения при условии, что матрица системы особенна, т. е. 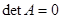 .
.
В общем случае решение однородной системы ранга 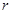 с
с 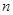 неизвестными
неизвестными
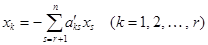 ,
,
где 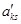 – элементы матрицы, преобразованной по алгоритму Гаусса – Жордана (предполагается, что основным неизвестным соответствуют первые
– элементы матрицы, преобразованной по алгоритму Гаусса – Жордана (предполагается, что основным неизвестным соответствуют первые 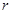 столбцов).
столбцов).
Рассмотрим однородную систему 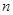 уравнений с
уравнений с 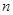 неизвестными
неизвестными 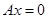 или
или 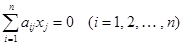 , матрица
, матрица 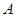 которой просто вырождена, т. е. ее ранг
которой просто вырождена, т. е. ее ранг 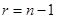 . Разлагая определитель этой матрицы по элементам какой-либо строки, запишем:
. Разлагая определитель этой матрицы по элементам какой-либо строки, запишем: 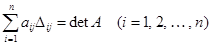 .
.
Так как 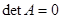 , то сравнивая записанные соотношения при любом
, то сравнивая записанные соотношения при любом 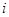 , находим
, находим 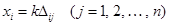 , где
, где 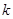 – произвольное число, не равное нулю. Таким образом, неизвестные пропорциональны соответствующим алгебраическим дополнениям элементов какой-либо строки матрицы
– произвольное число, не равное нулю. Таким образом, неизвестные пропорциональны соответствующим алгебраическим дополнениям элементов какой-либо строки матрицы 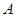 , т. е. вектор решений можно представить в виде:
, т. е. вектор решений можно представить в виде:
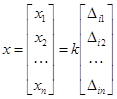 .
.
Решим систему уравнений
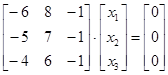 .
.
Матрица этой системы просто вырождена, так как ее ранг равен двум, следовательно, достаточно вычислить алгебраические дополнения элементов какой-либо строки, например, первой:
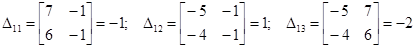 .
.
Отсюда запишем решение рассматриваемой системы уравнений: 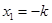 ;
; 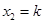 ;
; 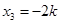 или
или 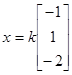 , причем это решение удовлетворяет данной системе при любом значении числа
, причем это решение удовлетворяет данной системе при любом значении числа 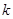 .
.
Дата добавления: 2016-09-06; просмотров: 4166;











