Общие дифференциальные уравнения гидростатики

(уравнения Л. Эйлера)

С помощью общих дифференциальных уравнений гидростатики определяется величина гидростатического давления в любой точке жидкости, находящейся в различных состояниях равновесия и покоя.

Для получения уравнений Эйлера рассмотрим случай относительного покоя жидкости, т.е. когда на жидкость действует не только сила тяжести, но и , например, силы инерции переносного движения.

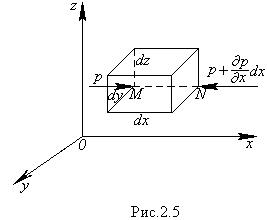
Возьмём в неподвижной жидкости точку М с координатами х ,у, z идавлением р. Выделим в жидкости элементарный объём в форме прямоугольного параллелепипеда, рёбра которого равны dx, dy, dz. При этом точка М пусть будет одной из его вершин (рис. 2.5).

Рассмотрим условия равновесия выделенного объёма, когда внутри параллелепипеда на жидкость действует равнодействующая массовая сила, составляющие которой, отнесенные к единице массы, равны X, Y и Z.

Вблизи точки М давление р одинаково по всем направлениям. В точке N оно получит приращение, равное частному дифференциалу и будет равно .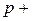

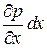Составим уравнение равновесия относительно оси Ох:

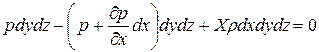. (2.15)

Раскроем скобки и сократим на массу, т.е. на 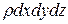, получим

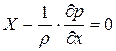. (2.16)

Аналогично составим уравнения равновесия относительно осей Оy и Oz. После проведенных преобразований получим

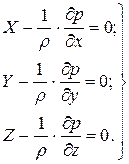(2.17)

Система уравнений (2.17) называется дифференциальными уравнениями равновесия жидкости, или уравнениями Эйлера.