Относительный покой жидкости

Мы рассмотрели основное уравнение гидростатики, являющееся решением дифференциальных уравнений равновесия Эйлера для частного случая – абсолютного покоя жидкости в поле сил земного (притяжения) тяготения. Возможны и другие случаи равновесия, в частности, относительный покой.

Относительным покоем называется состояние покоя относительно стенок сосуда, в котором находится жидкость. Сам же сосуд вместе с жидкостью может перемещаться относительно Земли. Например, в состоянии относительного покоя находится жидкость, помещённая в транспортные ёмкости – баки, цистерны и различные движущиеся сосуды. При относительном покое помимо сил тяжести, жидкости находятся ещё под воздействием сил инерции, которые также относятся к массовым или объёмным силам.

При рассмотрении состояния относительного покоя наибольший практический интерес представляет установление закона распределения давлений в конкретных случаях. Эти задачи решаются с помощью основного дифференциального уравнения гидростатики.

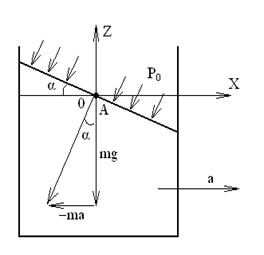
Рассмотрим относительный покой жидкости при прямолинейном равноускоренном движении сосуда.

Пусть сосуд с жидкостью, например, цистерна, движется в горизонтальном направлении с положительным ускорением, равным а.

Свободная поверхность жидкости нахо-

Рис. 2.7 дится под воздействием давления р₀. За начало координат примем точку О, лежащую на свободной поверхности жидкости в середине цистерны. Ось Ох направим в сторону движения, а ось Oz по вертикали вверх. Массовыми силами, отнесёнными к единице массы в области произвольно взятой точки А, являются сила тяжести g и сила инерции, равная по величине ускорению а, но направленную в противоположную сторону. Тогда, согласно основному дифференциальному уравнению гидростатики (2.20), проекции этих сил на оси координат будут равны:

x = -a; y =0; z = -g

В результате замены получим

dр = -ρ(adx + gdz), (2.32)

что после интегрирования даст

р = -ρ(ax + gz) + C. (2.33)

Данное выражение гидростатического давления справедливо для всех точек жидкости, в том числе и для точки О, расположенной на свободной поверхности в начале координат, где x = z = 0, p = p₀. В результате подстановки значений давления и координат в уравнение (2.33) определится постоянная интегрирования С = p₀. После замены значения С получим зависимость, определяющую гидростатическое давление в любой точке пространства, заполненного жидкостью.

p = p₀ – ρ(ax + gz). (*)

Поверхности равного давления, для которых dp = 0 и p = const согласно выражению (2.33) определяются уравнениями типа

ax + gz = const. (2.34) Следовательно, поверхности равного давления представляют собой плоскости, параллельные свободной поверхности и наклонные к оси Оx под углом α.

tg α =-a/g. (2.35)

Уравнение свободной поверхности жидкости, для которой p = p₀ выразится зависимостью

ax+gz=0. (2.36)

Таким образом, при движении с положительным ускорением жидкость сместится к задней стенке цистерны, как показано на рис.2.7. При отрицательном ускорении, то есть при торможении, сила инерции проектируется на ось Оx с положительным знаком и жидкость сместится в переднюю часть цистерны.

Следует отметить, что уравнение давления (*) по структуре совпадает с основным уравнением гидростатики и, следовательно, гидростатическое давление при относительном покое также равно сумме давления столба жидкости и давления на свободную поверхность.

В случае относительного покоя жидкости, находящейся в цилиндрическом сосуде, вращающемся вокруг своей оси гидростатическое давление в любой точке жидкости, находящейся в сосуде определяется по формуле:

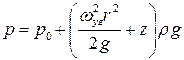, (2.37)

где 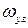– угловая скорость, с^-1; r – радиус цилиндра, м; p₀ – давление на свободную поверхность, Н/м²; z – вертикальная координата данной точки, м.