Вывод уравнения Эйлера для лопаточного насоса.

Вывод уравнения Эйлера выполним при следующих допущениях

ü - жидкость не сжимаема (ρ – const.);

ü - рабочее колесо вращается с постоянной частотой ω;

ü - рабочее колесо имеет бесконечно большое число лопаток (z=∞);

ü - толщина лопаток бесконечно мала (δ→0).

Принятые допущения позволяют рассматривать межлопаточный канал как элементарную струйку.

Определим количество движения жидкости в элементарной струйке на входе в рабочее колесо:

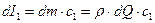, (1)

где dQ – расход жидкости через элементарную струйку;

Аналогично определим количество движения в элементарной струйке на выходе жидкости из рабочего колеса:

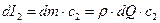(2)

Вычислим момент количества движения элементарной струйки

- на входе в рабочее колесо:

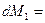
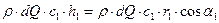; (3)

- на выходе из рабочего колеса:

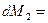
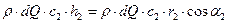. (4)

Определим изменение количества движения в струйке жидкости при переходе от входа к выходу:

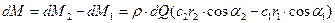(5)

Но , а 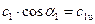, с учетом этого уравнение (5) перепишется в виде:

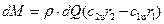. (5а)

Изменение момента количества движения всей массы жидкости, прошедшей через рабочее колесо за единицу времени, равно сумме изменений моментов количества движения во всех элементарных струйках:

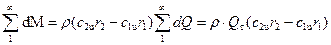, (6)

где 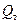- теоретический расход жидкости через все межлопаточные каналы рабочего колеса.

Из теоретической механики известно, что изменение момента количества движения системы равно моменту внешних сил, т.е. крутящему моменту, подведенному к колесу из вне: 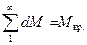. С учетом этого уравнение (6) перепишем в виде:

М_кр.= 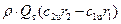(6а)

Умножив правую и левую части уравнения (6а) на угловую частоту ω получим выражение для мощности, затраченной на изменение момента количества движения жидкости, проходящей через рабочее колесо:

М_кр·ω=N= 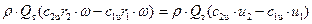(7)

Запишем выражение для мощности, выраженной через гидравлические параметры:

N=ρ·g·Q_т 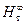, (8)

где 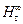- теоретический напор, создаваемый насосом с рабочим колесом с бесконечно большим числом лопаток бесконечно малой толщины.

Приравняв правые части уравнений (7) и (8) и решив полученное уравнение относительно теоретического напора, получим:

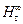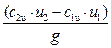= (9)

Уравнение (9) и есть уравнение Эйлера. В случае радиального входа жидкости на лопатки (cosα₁=90⁰=0) оно принимает более простой вид:

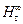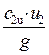= . (9а)