Контроллер (модель) типа Такаги-Сугено
Мы видели, что заключения в лингвистических моделях контроллеров являются нечеткими терм-множествами, однако они могут быть и четкими величинами, линейной комбинацией или даже нелинейной функцией четких входных сигналов. Общая структура N базовых правил Такаги-Сугено (ТС)для контроллера с r входами и одним выходом имеет следующий вид
Если e1 есть A1i, e2 есть A2i,…,er есть Ari, то yi = gi(e1, e2,…, er), 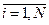 .
.
Здесь yi –выход (заключение) i-го правила, gi –четкаяфункция входов ei, 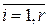 , которые в противоположность лингвистической модели всегда представляют собой четкие переменные. Простой пример (N=1).
, которые в противоположность лингвистической модели всегда представляют собой четкие переменные. Простой пример (N=1).
Если ошибка есть Нуль и скорость ее изменения есть Нуль, то выход u=c,
где c–не нечеткая (четкая) постоянная.
Эта модель называется моделью ТС нулевого порядка, и она идентична использованию синглтонов в заключениях правил, т.е. синглтонной модели. Несколько более сложное правило выглядит так:
Если ошибка есть Нуль и скорость ее изменения есть Нуль, то выход
u = a*( ошибка e) + b*( скорость изменения ошибки ce) + d,
где a, bиd– постоянные.
Это модель ТС первого порядка с одним правилом (N=1). Инференция с несколькими правилами осуществляется обычным способом, т.е. степень истинности (возбуждающая сила) 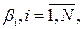 , вычисляется для каждого правила. Однако в отличие от рассмотренного ранее метода Мамдани заключение каждого правила
, вычисляется для каждого правила. Однако в отличие от рассмотренного ранее метода Мамдани заключение каждого правила 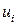 является линейной функцией входов, например, ошибки и скорости ее изменения
является линейной функцией входов, например, ошибки и скорости ее изменения
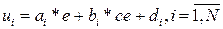 .
.
Заключение (выход) каждого правила можно рассматривать как мобильный синглтон, т. е. как синглтон, позиция которого не фиксирована, а зависит от текущих значений ошибки и скорости ее изменения. Выход (заключение) всех правил в этом методе в результате дефаззификации определяется как взвешенное среднее значение вкладов (метод центра тяжести), вносимых каждым правилом
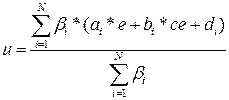 .
.
Лекция 16
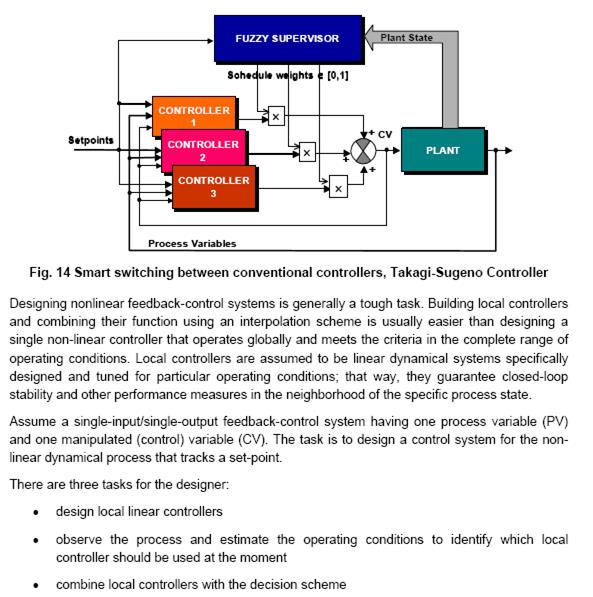
Такой контроллер, можно сказать, осуществляет нелинейную интерполяцию выходных сигналов N линейных контроллеров (рис. 1), каждый из которых в соответствии с одним из базовых правил вырабатывает сигнал, линейно зависящий, скажем, от ошибки и ее скорости изменения. При этом вклад каждого линейного контроллера в выходной сигнал нелинейного контроллера зависит от степени перекрытии ФП терм-множества входа. Это свойство весьма полезно для применения в нелинейных системах управления, где каждый контроллер работает лишь в отведенном ему
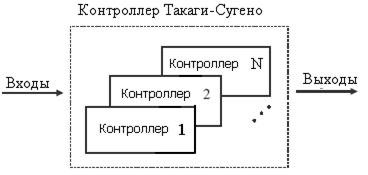
Рис. 1
подпространстве всего пространства состояний. Можно сказать, что базовые правила осуществляют плавную интерполяцию между плоскостями (в частном случае для одного входа (r=1) между прямыми линиями, см. рис. 2,а), наклон которых определяется коэффициентами линейных контроллеров.
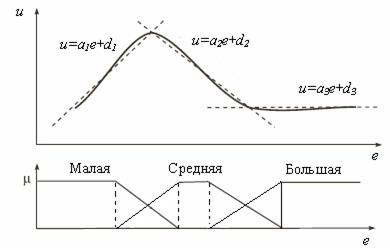
Рис. 2,а
На рис. 2,б в качестве примера для N=4, r=2 показаны желтым цветом плоскости управления для 4-х линейных контроллеров и поверхность управления для контроллера Такаги-Сугено первого порядка при двух термах для каждого входа с трапециидальными функциями принадлежности.
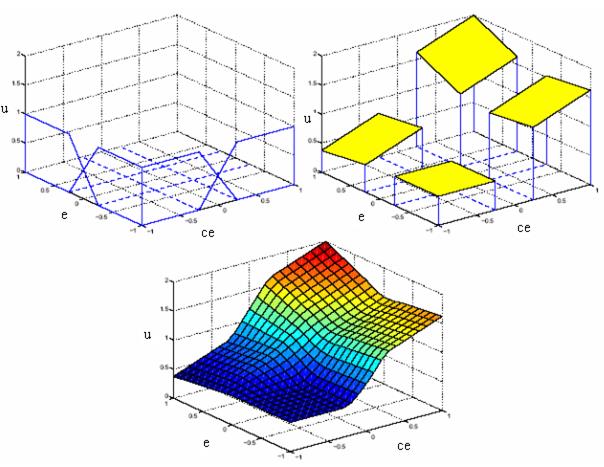
Рис. 2,б
Заметим, что возможно применение моделей ТС более высокого порядка, чем первый.
Если ФП терм входов определены автономно, кроме участков перекрытия друг с другом, и параметры заключений 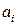 ,
, 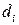 соответствуют локальной аппроксимации функции u=f(e), r=1, N=3, модель ТС можно рассматривать как устройство, осуществляющее гладкую аппроксимацию этой функции (рис. 2,а).
соответствуют локальной аппроксимации функции u=f(e), r=1, N=3, модель ТС можно рассматривать как устройство, осуществляющее гладкую аппроксимацию этой функции (рис. 2,а). 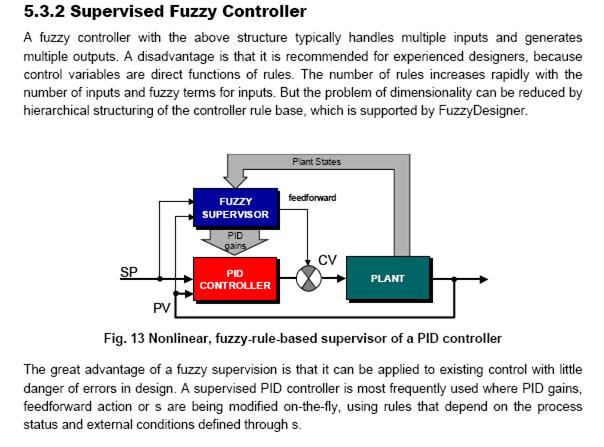



Дата добавления: 2021-01-11; просмотров: 692;











