Модель Такаги-Сугено как квазилинейное устройство

Модель ТС можно трактовать как квазилинейное (аффинное) устройство. Чтобы это показать, преобразуем выражение для выхода:

где коэффициенты

, ,

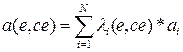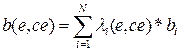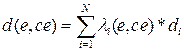
представляют собой линейные комбинации параметров 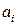, , 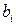, 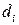а величина

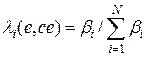
является нормированной степенью истинности (возбуждающей силы) i-го правила. Мы записали 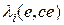явно как функцию e и ce , чтобы подчеркнуть, что контроллер Такаги-Сугено является квазилинейной (аффинной) моделью, т.е. линейной моделью, коэффициенты которой зависят от входных сигналов.

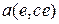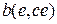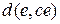Коэффициенты («параметры») , и являются выпуклой линейной комбинацией параметров заключений 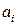, , 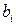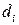. В этом смысле модель (контроллер) ТС можно рассматривать как устройство, преобразующее пространство входов (условий) в пространство параметров квазилинейной модели, как схематически показано на рис. 4 для r=2, N=9, 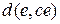=0.

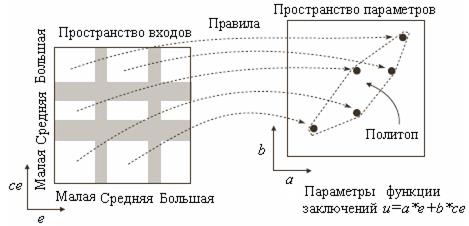
Рис. 4

Примечание. Политоп – выпуклый многогранник.

Пример 2.4 (Такаги-Сугено). Пусть мы имеем два правила.

1. Если ошибка есть Большая, то выход есть Линия 1.

2. Если ошибка есть Малая, то выход есть Линия 2.

Линия 1 определяется уравнением 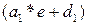=0,2*ошибка+90 и линия 2 определяется как 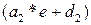=0,6* ошибка +20. Эти правила осуществляют интерполяцию двух линий в диапазоне (рис. 5,a), где функции принадлежности термов Большая и Малая перекрываются (рис. 5,б). Вне этого диапазона выход является линейной функцией ошибки.

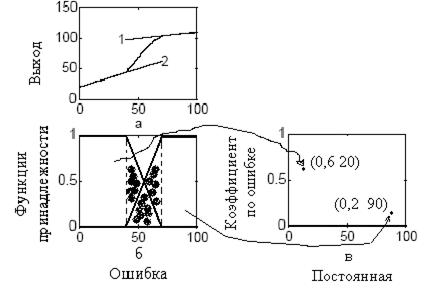
Рис. 5

Этот вывод вытекает из выражения для выхода

.

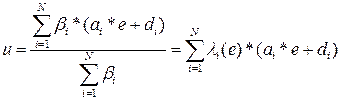Подобный вид модели нечеткого логического выхода используется в нейронечетких системах.

Чтобы применить данную модель, точнее нейронечеткую систему, для моделирования динамики конкретного объекта управления, ее вход обычно расширяют за счет прошлых значений сигналов входа u и выхода y этого объекта. В области дискретного времени выход модели y^m с верхним индексом, относящимся к модели, и выход объекта y^p с верхним индексом, относящимся к объекту, связаны как

y^m[i+1] = 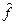(y^p[i],…, y^p[i − n+1];u[i],…, u[i − m+1]).

Здесь 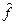представляет собой нелинейную функцию, связывающую выход и вход модели (т.е. аппроксимацию функции f, связывающей выход и вход этого объекта). Разумеется, что речь идет о дискретной модели объекта управления, как это видно из уравнения для y^m[i+1].