Табличное изменение коэффициента усиления (супервизорное управление)
Рассмотрим использование контроллера Такаги-Сугено для супервизорного управления, понятие о котором было дано в параграфе 2.1. Пусть объект управления с существенно нелинейными свойствами (коэффициент усиления объекта y2(t) зависит от управляемой величины y(t)) описывается уравнением
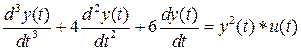 .
.
Структуру данного объекта можно представить как линейная часть с передаточной функцией
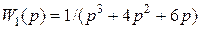 ,
,
охваченная квадратичной обратной связью (рис.6).
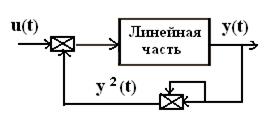
Рис. 6
Цель управления заключается в том, чтобы обеспечить стабилизацию системы при изменении рабочей точки (состояния равновесия), т.е. значения y=const, в широких пределах при условии, что y 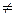 0. Проблемы, возникающие при использовании для этой цели четкого пропорционального регулятора с фиксированным коэффициентом усиления kp, сводятся к следующему:
0. Проблемы, возникающие при использовании для этой цели четкого пропорционального регулятора с фиксированным коэффициентом усиления kp, сводятся к следующему:
1) устойчивость и качество системы в сильной степени зависят от значения управляемой величины в состоянии равновесия;
2) настройка (подбор) коэффициента усиления kp не позволяет добиться желаемой цели.
Отсюда приходим к выводу, что единственный путь решения поставленной задачи применить нелинейный закон управления, а именно, супервизорное управление, которое бы изменяло коэффициент усиления по нелинейному закону в зависимости от управляемой величины у. Предположим, что мы нашли желаемый закон изменения коэффициента усиления регулятора, обеспечивающий требуемое качество управления (рис.7).
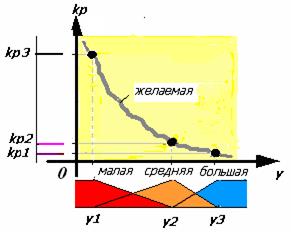
Рис. 7
Для реализации желаемого закона управления можно использовать различные способы аппроксимации, в частности, кусочно-линейную аппроксимацию или метод задания таблиц (look-up table) . Однако более удобно с точки зрения точности и быстроты вычислений применить нечеткий контроллер типа Такаги-Сугено. Заметим, что с помощью нечеткой логики можно, используя правила и функции принадлежности обеспечить аппроксимацию любой непрерывной функции с любой требуемой точностью, т.е. нечеткая модель Такаги-Сугено (ТСМ) при соответствующем выборе параметров является универсальным аппроксиматором непрерывной вещественной функции, которая определена в замкнутом и ограниченном множестве Rn . Это означает, что для любого 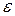 >0 и для любой непрерывной функции g(x) существует ТСМ такая, что g(x) - y(x) <
>0 и для любой непрерывной функции g(x) существует ТСМ такая, что g(x) - y(x) < 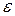 , где y(x) является выходом ТСМ.
, где y(x) является выходом ТСМ.
Рис. 7 иллюстрирует, каким образом можно аппроксимировать желаемую кривую изменения коэффициента усиления регулятора, используя три точки (другими словами, три правила) и тем самым осуществить супервизорное управление. Разумеется, чтобы повысить точность аппроксимации (подобно тому, как это делается в ряде Фурье), нужно еще добавить точки, и следовательно, правила, которые очевидно улучшат качество управления. Нечеткий контроллер, используемый для аппроксимации, значительно проще реализовать и настроить с помощью средств вычислительной техники, чем таблицы задания и кусочно-линейный аппроксиматор.
В данном случае базовые правила выглядят так:
Если управляемая величина y большая, То коэффициент kp1,
Если управляемая величина y средняя, То коэффициент kp2,
Если управляемая величина y малая, То коэффициент kp3.

Рис. 7
При этом
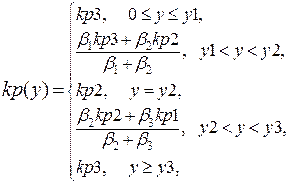
Правила не аналогичны методу заданию таблиц, т.к. нечеткая арифметика интерполирует форму нелинейной функции. Показано, что объем памяти, требуемый для сохранения информации о функциях принадлежности и правил, значительно меньше, чем для таблиц задания, в особенности для систем с несколькими входами. В результате скорость вычислений может быть также повышена.
Лекция 17
Пример 2.5 (Супервизорное управление).Симуляция модели (рис. 8) системы супервизорного управления при kp5=32; kp4=8; kp3=3,55; kp2=2; kp1=0,5; y1 =0,5; y2=1; y3=1,5; y4=2; y5=4и системы с пропорциональным законом управления с фиксированным коэффициентом kp4=8 для v(t)=2*1(t) и v(t) = 1(t) показывают (рис. 9, 10), что использование нелинейного закона управления
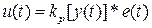
позволяет обеспечить стабилизацию системы в широком диапазоне изменения управляемой величины (модель supervisor.mdl в MATLABR2006a).
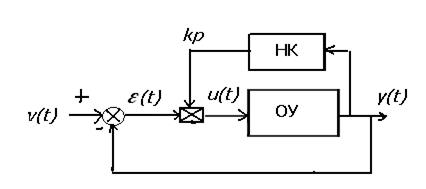
Рис. 8
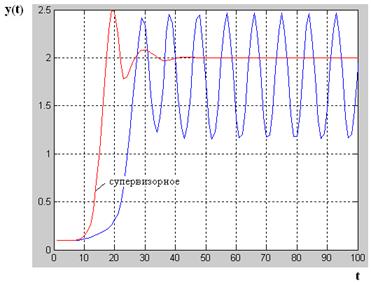
Рис. 9
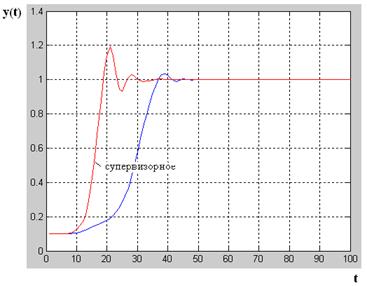
Рис. 10
Дата добавления: 2021-01-11; просмотров: 641;











