Аппроксимация функций с помощью нейронных сетей

Рассмотрим задачу реализации нелинейных алгебраических зависимостей нейронными сетями. Приведенный выше персептрон может аппроксимировать

произвольную гладкую функцию. В качестве примера запишем выходной сигнал сети с одним выходом y и одним входом u, состоящей из одного скрытого слоя с двумя нелинейными нейронами и выходного слоя из одного линейного нейрона:

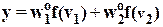. (28)

Внутренние входы v₁ и v₂ скрытых нейронов определяются выражениями

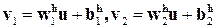. (29)

Пусть функция активации f (v) скрытых нейронов является функцией tangh(v)(гиперболический тангенс). При этом график зависимости y=g(u)принайденных в результатеобучения значениях весовых коэффициентов w⁰ , w^h и смещений b^hможно построить, как показано на рис. 8. Здесь 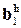= 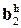, 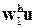= - 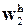, 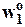= =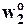1.

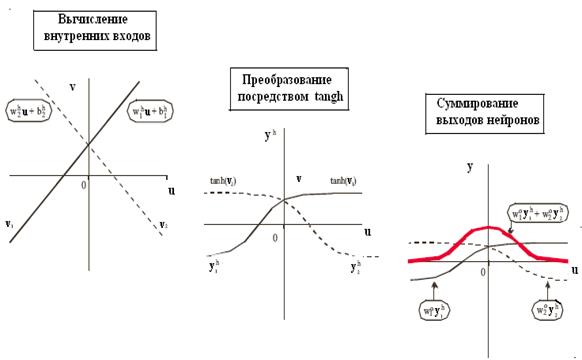
Рис. 8

Изменяя веса и смещения в соответствии с обучающей выборкой, получаем гладкую кривую, аппроксимирующую вход нейронной сети.

Эффективность использования нейронных сетей устанавливается теоремой

о полноте. Смысл этой теоремы в том (Cybenko, 1989), что персептрон, по

меньшей мере с одним скрытым слоем, способен аппроксимировать любую

непрерывную функцию 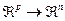с произвольной степенью точности при условии

выбора достаточного числа нейронов скрытого слоя.