Преобразование нечеткого линейного контроллера в нелинейный

Четвертый шаг в процедуре проектирования постепенно преобразовать линейный нечеткий контроллер в нелинейный. Общепринятая практика сформировать базовые правила, используя такие термы, как Пол, Нуль и Отр, которые являются названиями (ярлыками, лейблами) нечетких множеств. Пусть входное терм-множество состоит из этих трех терм. Следовательно, при двух входах надо сформировать 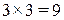правил. Девять правил представляют собой легко корректируемое количество, часто применяемое на практике. Форма функций принадлежности и сформированные правила определяют закон управления и следовательно, динамику замкнутой системы. Существенными являются четыре характерные формы поверхностей управления.

· Линейная поверхность (рис. 3, слева) является результатом применения нижеприведенных базовых правил при треугольной форме функций принадлежности для всех термов входов,

1. Если ошибка Отр и скорость изменения ошибки Отр, то выход –200;

2. Если ошибка Отр и скорость изменения ошибки Нуль, то выход –100;

3. Если ошибка Отр и скорость изменения ошибки Пол, то выход 0;

4. Если ошибка Нуль и скорость изменения ошибки Отр, то выход –100;

5. Если ошибка Нуль и скорость изменения ошибки Нуль, то выход 0;

6. Если ошибка Нуль и скорость изменения ошибки Пол, то выход 100;

7. Если ошибка Пол и скорость изменения ошибки Отр, то выход 0;

8. Если ошибка Пол и скорость изменения ошибки Нуль, то выход 100;

9. Если ошибка Пол и скорость изменения ошибки Пол, то выход 200.

При построении поверхности используется метод, когда множества (термы) выхода выбраны в виде синглтонов. В соответствии с этим методом выходу контроллера соответствуют конкретные численные значения (-200, -100, 0, 100 и 200). Поверхность на рис. 3, слева эквивалентна суммированию двух входных сигналов (см. названия осей координат). При такой поверхности нечеткий контроллер эквивалентен четкому ПД-регулятору.

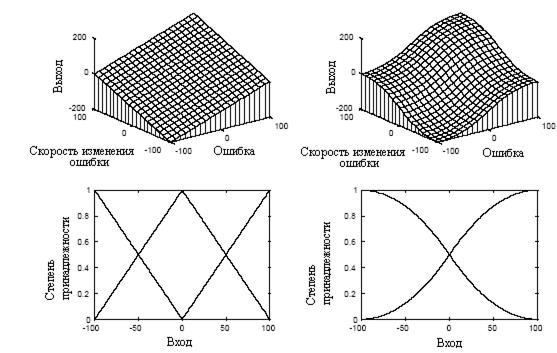
Рис. 3

· Крутая поверхность (рис. 3, справа) построена с использованием правил 1, 3, 7 и 9 совместно с термами Пол и Отр, функции принадлежности которых показаны на рис. 3, справа внизу; эти функции представляют собой сегменты косинусной функции. Обратите внимание на отсутствие среднего правила 5 с термами Нуль для ошибки и скорости изменения ошибки. Эта поверхность имеет более крутой уклон в центре, отсюда более высокий коэффициент усиления в центре таблицы, чем линейная; однако обе упомянутые поверхности в 4 углах попарно имеют одинаковые уклоны.

· Пологая поверхность (рис. 4, слева) построена, с учетом тех же 4 правил 1, 3, 7, 9, но функции принадлежности терм входов являются зеркальными отображениями функций принадлежности терм входов для крутой поверхности. Они представляют собой обратные тригонометрические функции: Пол(x)=0,5+arcsin(x/100)/π, а Отр(x)=arсcos(x/100)/π. Эта поверхность имеет более пологий уклон в центре, чем линейная, но так же, как и они имеет в углах попарно одинаковые уклоны.

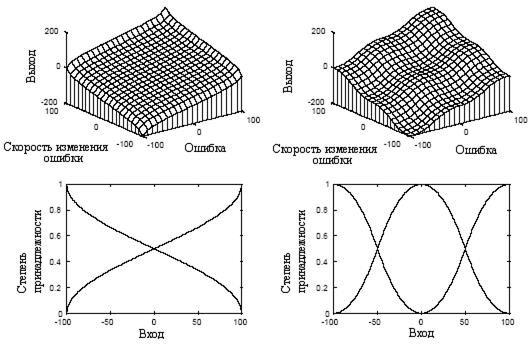
Рис. 4

· Ухабистая поверхность (рис. 4, справа) является композицией двух предыдущих поверхностей. Она построена с использованием всех 9 правил с нелинейными функциями принадлежности, показанными на рис. 4, справа внизу. Очень часто используют именно ее по умолчанию. Для нее характерны плоский участок (плато) в центре и неровности (ухабы) в некоторых других местах. Даже эта поверхность в четырех углах имеет те же самые уклоны, что и другие поверхности.

Следует отметить, что трудно сделать строгое, беспристрастное и объективное сравнение свойств рассмотренных поверхностей относительно показателей качества систем управления, многое зависит от свойств объекта.

Лекция 15